Lösungen anderer Jahre:
2008	2009	2010	2011	2012	2013	2014	2015	2016	2017	2018	2019	2020

Lösung des Preisrätsels vom Dezember 2008:

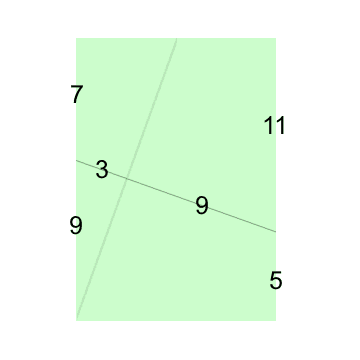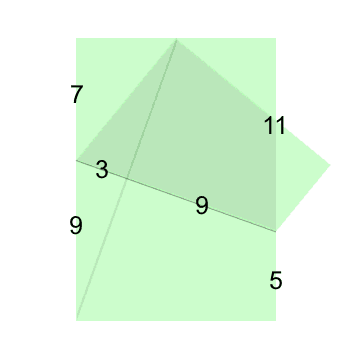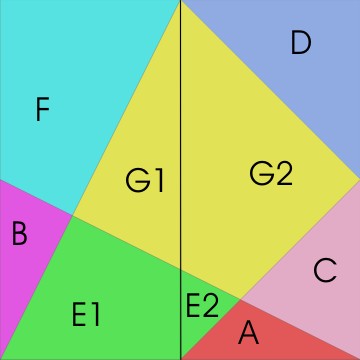
Teilflächen des Quadrats Die Hilfslinie, die das Quadrat senkrecht halbiert, vereinfacht den Lösungsweg (siehe Bild links). Die nun vorhandenen 9 Flächen sind mit einem nicht ganz simplen, aber übersichtlichen Gleichungssystem zu beschreiben (gesamte Quadratfläche = 1): B + F = 1/4 F = 4 • B G1 + E1 = 1/4 B + E1 = 3/16 D = 1/8 G2 + E2 = 1/4 A + C = 1/8 C = 4 • E2 E2 + A = 1/16 Der gemeinsame Hauptnenner der Einzelergebnisse ist 120 und die Zähler ergeben dann die Lösung: A:B:C:D:E:F:G = 5:6:10:15:19:24:41 nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom November 2008:

Kepplertafel in Ulm Bei diesem Rätsel musste der Fehler im Bild gefunden werden (siehe nebenstehendes Bild mit blinkenden Stelle). Es war ein Zahlendreher in der Jahreszahl 1627. Auf dem Weg zur Ringförmigen Sonnenfinsternis in Spanien 2005 machte  wissenschaftsreisen.de  auch einen Stopp in Ulm, wo auf der Seitenwand des Rathauses mit der berühmten Astronomischen Uhr diese Tafel zu sehen war. nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom Oktober 2008:

Mansfeld-Museum in Hettstedt Bei diesem Rätsel mußte der Fehler im Bild gefunden werden (siehe nebenstehendes Bild mit blinkenden Stelle). Es war der veränderte Schriftzug auf dem 'Mansfelder Hunt' des Mansfeld-Museums. Anlässlich des Wiedersehenstreffens in Aschersleben 2003 stand auch ein Besuch mit  wissenschaftsreisen.de  in diesem Museum auf dem Programm, wo unter anderem die erste deutsche Dampfmaschine nach Wattscher Bauart ausgestellt ist. nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom September 2008:
	Sonnensystem-Sudoku Die Lösungsfolge der Sonnenpositionen in den Reihen von oben nach unten ist: 1, 7, 5, 2, 6, 8, 3, 9, 4  wissenschaftsreisen.de  nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom August 2008:

durchbohrte Kugel Da bei diesem Rätsel der Radius der Kugel nicht angegeben war, und man weiterhin darauf vertrauen konnte, dass es eine Lösung gibt, so ist diese Lösung unabhängig vom gewählten Radius. Man wähle also den Grenzfall rG = halbe Bohrtiefe mit unendlich dünnem Bohrer und erhält als 'Restvolumen' das Volumen der Kugel mit Radius rG. Wem diese Kurzform verdächtig erscheint, der kann den Weg des vollständigen Beweises links verfolgen. Auf der Mathematischen Reise im Juli 2008 mit  wissenschaftsreisen.de  sind solche und ähnliche Dinge in verschiedenen Museen handgreiflich zu erfassen. nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom Juli 2008:

Papier Faltung Die Lösung lautet: a:b:c:d:e = 5:7:9:11:12 siehe nebenstehende Zeichnung Interessant ist, dass keine irrationalen Zahlen bei diesen Verhältnissen auftauchen und selbst die Teilung der Strecke e durch die Verbindungslinie von der unteren linken Ecke zur Mitte der oberen Seite ganzzahlig ist. Das alles bei einem Seitenverhältnis des Blattes von 1.4142135623 7309504880 1688724209 6980785696 ... Auf der Mathematischen Reise im Juli 2008 mit  wissenschaftsreisen.de  sind solche und ähnliche Dinge in verschiedenen Museen handgreiflich zu erfassen. nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom Juni 2008:

1.) 652 = 162 + 632 4225 = 256 + 3969 2.) 652 = 252 + 602 4225 = 625 + 3600 3.) 652 = 332 + 562 4225 = 1089 + 3136 4.) 652 = 392 + 522 4225 = 1521 + 2704

Pythagoräische Dreiecke Die Lösung lautet: 65 (siehe Tabelle links) Von allen ganzen Zahlen als Hypothenusen lassen sich in 28% gar keine, in 44% nur eine, in 1,9% genau zwei, in 0,33% genau drei und in 20% genau vier Zerlegungen angeben. Man kann aber leicht für jede vorgegebene Zerlegungsanzahl n eine ganzzahlige Hypotenuse angeben, nämlich 5n. Das ist aber selten die kleinste Lösung. Auf der Mathematischen Reise im Juli 2008 mit  wissenschaftsreisen.de  werden auch solche und ähnliche Dinge behandelt. nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom Mai 2008:

Geostationären Satelliten Wären die Radien der Umlaufbahnen unendlich groß, ähnlich wie die Sterne auf dem Himmelsäquator, so würde man die Satelliten am Nordpol genau am idealen Horizont sehen. Tatsächlich kann man wegen der Refraktion noch etwa ein Grad unter den Horizont sehen. Aber das reicht für die geostationären Satelliten bei weitem nicht, denn sie stehen mehr als 8,56 Grad unter dem Horizont, sie sind also alle "unsichtbar". Die Lösung lautet: keine, 0, oder null Ein Besuch in der Fundamentalstation Wettzell im November 1999 mit  wissenschaftsreisen.de  informierte über Ergebnisse und Techniken zur Satelliten-Distanz-Messungen und GPS. nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom April 2008:

Verteilung der Osterdaten Die nebenstehende Verteilung ist vielleicht überraschend, aber symmetrisch wäre sie nur, wenn es in der Gauss'schen Osterformel keine Ausnahmeregel gäbe, die den 26. April als Ostertermin verbietet. Papst Gregor XIII. konnte den 26. April nicht zulassen, weil auch im Julianischen Kalender dieser Ostertermin nicht existierte. Nach wie vor hat der Vatikan bis heute die Oberhoheit über das Osterdatum, was wir bei einem Besuch von  wissenschaftsreisen.de  im Oktober 1998 in der Sommerresidenz des Papstes erleben durften. Die Lösung lautet also: 19. April 2071 nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom März 2008:
	Der Kalenderstein der Azteken besucht von  wissenschaftsreisen.de  anlässlich einer Studienreise nach Mexiko vom 11. bis 26. März 2001. Das nebenstehende Bild musste durch Verschieben der 24 Einzelteile entstehen. Das Lösungswort (eine Zahl mit Prüfziffern) wurden bei Vollendung automatisch erzeugt. nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom Februar 2008:
	Die Himmelsscheibe von Nebra besucht von  wissenschaftsreisen.de  und das Original in die Hand genommen anlässlich des Wiedersehenstreffens in Aschersleben 2003. Das Bild der Himmelsscheibe musste durch Verschieben der 24 Einzelteile entstehen. Das Lösungswort (eine Zahl mit Prüfziffern) wurden bei Vollendung automatisch erzeugt. nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom Januar 2008:
	Die Astronomische Uhr im Dom zu Münster besucht von  wissenschaftsreisen.de  anlässlich des Wiedersehenstreffens in Münster 2004. Das nebenstehende Bild musste durch Verschieben der 24 Einzelteile entstehen. Das Lösungswort (eine Zahl mit Prüfziffern) wurden bei Vollendung automatisch erzeugt. nochmal zurück zu diesem Rätsel

Lösungen anderer Jahre:
2008	2009	2010	2011	2012	2013	2014	2015	2016	2017	2018	2019	2020