Lösungsbeschreibung des Preisrätsels vom März 2020

Zykloiden

1.) der Weg zur Lösung

Für die Lösung dieses Rätsels gib es einen hoch theoretischen Weg über elliptische Integrale der 2. Art, aber der führt nicht sehr weit. Es gibt keine einfache Formel sondern nur Reihenentwicklungen, die mehr oder weniger gute Näherungen sind. Ich werde später noch auf diesen Lösungsweg eingehen.

Der praktische Weg bestimmt die Koordinaten vieler Punkte auf der Kurve und berechnet die Abstände zum Nachbarpunkt. Die Summe dieser Abstände ist näherungsweise die untere Grenze der Kurvenlänge, weil nur die Sehnenlängen aufsummiert werden (Polygonzug).

2.) die Funktionsgleichung einer Zykloide

Ein Koordinatenpunkt auf einer Zykloide ist leicht zu berechnen. Es ist der Endpunkt eines Ortsvektors $\vec {v}$, der aus der Summe zweier Vektoren sich ergibt: dem mit $\alpha$ länger werdenden horizontalen Vektor $\vec {v_1}$ und dem am Endpunkt des ersten mit $\alpha$ rechts herum kreisende Vektor $\vec {v_2}$. $$ \vec {v_1}=(x_1,y_1)=(\alpha \cdot r_1,r_1) \\ \vec {v_2}=(x_2,y_2)=(-\sin\alpha \cdot r_2,-\cos\alpha \cdot r_2) \\ \vec {v}=(x,y)=\vec {v_1}+\vec {v_2}=(\alpha \cdot r_1-\sin\alpha \cdot r_2,r_1-\cos\alpha \cdot r_2) $$ Dabei sind die Radien $r_1$ und $r_2$ aus den Abständen der Höhen der Punkte zu berechnen: $$ r_1=\text{Höhe des blauen Punktes, die Achse des Rollrades}=0,400\,m \\ r_2 (\text{für rot})=\text{Abstand des roten zum blauen Punkt}=0,000-0,400\,m=-0,400\,m \\ r_2 (\text{für blau})=\text{Abstand des blauen zum blauen Punkt}=0,400-0,400\,m=0,000\,m \\ r_2 (\text{für violett})=\text{Abstand des violetten zum blauen Punkt}=0,580-0,400\,m=0,180\,m \\ r_2 (\text{für grün})=\text{Abstand des grünen zum blauen Punkt}=0,856-0,400\,m=0,456\,m \\ $$

3.) die EXCEL-Tabelle zur Berechnung

Die Genauigkeit nimmt mit der Anzahl der Punkte zu. Gegenläufig nimmt die Genauigkeit wegen der Rundungsfehler ab. Deshalb ist auf die Genauigkeit der Arithmetik Rücksicht zu nehmen.

Eine EXCEL-Tabelle lässt sich sehr leicht vergrößern, aber man sollte es nicht übertreiben. In diesem Beispiel reichen 181 Punkte im Abstand von 1° für den Parameter α, denn die Zykloide ist spiegelsymmetrisch und so reicht es, nur die erste Hälfte der Länge zu berechnen und das Ergebnis wird am Ende verdoppelt.

Die Berechnung in der n-ten EXCEL-Zeile ist: $$ \alpha_n =n \cdot\pi/180 \\ x_n=\alpha_n \cdot r_1-\sin\alpha_n \cdot r_2 \\ y_n=r_1-\cos\alpha_n \cdot r_2 \\ d_n=\sqrt{(x_n-x_{n-1})^2+(y_n-y_{n-1})^2} $$

r1 = 0,4 und r2 = -0,400 (rote Zykloide)
n	αn	xn	yn	dn (Abstand zum Vorgänger)
0	0,0000	0,00000000000000	0,80000000000000	0,00000000000000
1	0,0175	0,01396227958289	0,79993907806256	0,01396241249331
2	0,0349	0,02792243269696	0,79975633080764	0,01396134920154
⋮	⋮	⋮	⋮	⋮
178	3,1067	1,25663422610096	0,00024366919236	0,00030459133572
179	3,1241	1,25663670700285	0,00006092193744	0,00018276409400
180	3,1416	1,25663706143592	0,00000000000000	0,00006092296845
Summe aller Abstände: 1,59999492			Länge des Polygonzugs: 3,19998985 (-0,00081 %)

Tabelle 1

	rot	blau	violett	grün
verkürzte Tabelle
vollständige Tabelle

Mit der obigen Auswahl lässt sich die Tabelle 1 anpassen und so die Ergebnisse für die Rätselfragen erhalten. Die Genauigkeit (in Klammern) wird durch die hier geringe Anzahl an Sehnen begrenzt. Im Folgenden werden bessere Möglichkeiten gezeigt.

4.) die Integralmethode zur Berechnung

Die Standardmethode zur Berechnung einer Kurvenlänge $s$ in parametrischer Darstellung ist das bestimmte Integral: $$ s=\int _{t_1}^{t_2}{\sqrt {\left({\frac {dx}{dt}}\right)^{2}+\left({\frac {dy}{dt}}\right)^{2}}}\;dt \tag{1} $$ Dabei ist im Fall einer Zykloide die untere Grenze $0$ und die obere Grenze $2\pi$. Die Variable ist nicht $t$ sondern $\alpha$. $$ x(\alpha)=\alpha \cdot r_1-\sin\alpha \cdot r_2 \\ y(\alpha)=r_1-\cos\alpha \cdot r_2 \\ \,\\ \,\\ x'=\frac{dx}{d\alpha}=r_1-\cos\alpha\cdot r_2 \\ y'=\frac{dy}{d\alpha}=\sin\alpha\cdot r_2 \\ \,\\ \,\\ {x'}^2={r_1}^2-2r_1r_2\cdot \cos\alpha+\cos^2\alpha\cdot {r_2}^2 \\ {y'}^2=\sin^2\alpha\cdot {r_2}^2 \\ \,\\ \,\\ {x'}^2+{y'}^2={r_1}^2-2r_1r_2\cdot \cos\alpha+{r_2}^2 $$ Wenn wie bei der roten Zykloide $r=r_1=r_2$ ist, kann man das Integral lösen: $$ {x'}^2+{y'}^2=2r^2-2r^2\cdot \cos\alpha \\ \sqrt{ {x'}^2+{y'}^2}=r\cdot\sqrt{2-2\cdot\cos\alpha} \\ s=\int _{0}^{2\pi }r\cdot\sqrt {2-2\cdot\cos \alpha}\;d\alpha \\ s=2r\cdot\int _{0}^{2\pi }\sin {\frac {\alpha}{2}}\;d\alpha=8r $$ und erhält damit die Länge der roten Zykloide zu $8r=8\cdot 0,4\,m=3,2\,m$

Für alle Fälle mit $r1≠r2$ gilt: es ergibt sich ein elliptisches Integral der 2. Art und dies ist nicht einfach lösbar.

Aber man kann das Integral in eine unendliche Summe verwandeln und danach als Näherung eine endliche Summe bilden, mit mehr oder weniger vielen Summanden, wie auch oben die Kurve in Tabelle 1 in viele Sehnen umgewandelt und deren Summe eine untere Annäherung für die Länge einer Zykloide ist. Nimmt man die aus dem Integral (2) abgeleitete Summe, geht man den Weg nicht über Sehnen der Kurve sondern über Tangenten und erhält eine obere Annäherung. $$ s=\int _{0}^{2\pi } \sqrt { {r_1}^2-2r_1r_2\cdot \cos\alpha+{r_2}^2}\;d\alpha \tag{2} $$

5.) die EXCEL-Makrofunktion zur Berechnung

Aber EXCEL kann nicht nur mit Hilfe des Tabellenblatts komplexe Probleme lösen. Es gibt darüber hinaus noch die Makrofunktionen (VBA = Visual Basic for Applications). Das ist eine vollständige Programmiersprache, die vom Tabellenblatt ausgehend selbst programmierte Funktionen und Prozeduren aufrufen kann.

Für die Bestimmung der Länge einer Zykloide wird eine Funktion geschrieben, der man Parameter mitgeben kann, z.B. r1 und r2 sowie die Anzahl der Abschnitte eines Polygonzuges. Diese wird, wie jede andere interne EXCEL-Funktion auf dem Tabellenblatt in eine Zelle eingeschrieben und liefert als Ergebnis einen Zahlenwert.

Es ist eine Funktion mit Namen "unter" als Nachbildung der obigen Tabelle erstellt worden, die eine untere Grenze der Länge erzeugt: Man hat die Möglichkeit, neben den Radien auch die Anzahl der Abschnitte vorzugeben. Das ermöglicht auch sehr große Anzahlen einzugeben wie es eine Tabelle wie oben niemals schaffen kann.

Untergrenze (rot)
n	r2	s
10	-0,400	3,19673756227096
100	-0,400	3,19996710562104
1000	-0,400	3,19999967101377
10000	-0,400	3,19999999671013
100000	-0,400	3,19999999996712
1000000	-0,400	3,19999999999981

Auch eine Funktion abgeleitet vom Integral (2) für die Obergrenze liegt vor:

Obergrenze (rot)
n	r2	s
10	-0,400	3,20329223725667
100	-0,400	3,20003289891810
1000	-0,400	3,20000032898684
10000	-0,400	3,20000000328988
100000	-0,400	3,20000000003290
1000000	-0,400	3,20000000000048

6.) alle Zykloiden-Längen auf dem EXCEL-Blatt

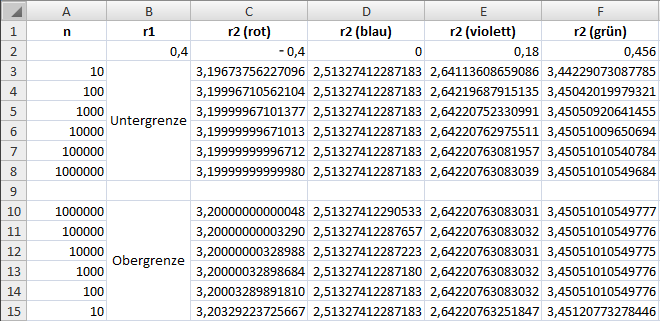
Bild 1

7.) Abschließende Bemerkungen

Die Konvergenz der Rechnung für die verschiedenen Zykloiden ist unterschiedlich. Die besseren Werte liefert das Makro für die Obergrenze. Aber man sieht auch an den Zahlenwerten der blauen Zykloide, dass man nicht immer mit größerem n bessere Ergebnisse bekommt. Hier führt der Rundungsfehler zu einem systematischen Fehler weil alle Summanden gleich groß und damit der Fehler sich mit n vervielfacht. Bei den anderen Zykloiden gibt es eine statistische Verteilung zwischen Auf- und Abrundung und der Fehler wächst nicht im gleichen Maß mit n an.

Wenn man genauere Lösungen benötigt muss eine bessere Arithmetik benutzt werden. In der webbasierten Programmiersprache PHP gibt es eine solche mit beliebiger einstellbarer Genauigkeit. Die Rechengeschwindigkeit wird aber deutlich langsamer. Damit sind die folgenden Werte berechnet worden:

Linienfarbe	Linienlänge in m
rot	3,2000000000000000000000000000000
blau	2,5132741228718345907701147066236
violett	2,6422076308303219839212198247750
grün	3,4505101054977579612269633900744

Diese Informationen wurden zusammengestellt von