1.) Voraussetzungen
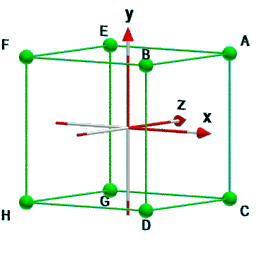Gegeben sind die acht Eckpunkte eines Würfels mit den folgenden Koordinaten:
$$\begin{align}
A&=(1,1,1) \quad
&B&=(1,1,-1) \\
C&=(1,-1,1) \quad
&D&=(1,-1,-1) \\
E&=(-1,1,1) \quad
&F&=(-1,1,-1) \\
G&=(-1,-1,1) \quad
&H&=(-1,-1,-1)
\end{align}$$
Das entspricht einem Würfel mit der
$$\rand{
Kantenlänge=2
}$$
2.) Netzwerk ohne zusätzliche Knoten
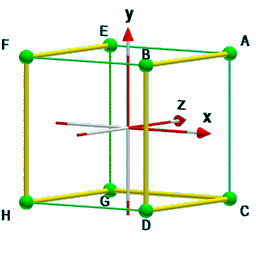Die acht Eckpunkte des Würfels können mit sieben geraden Linien zu einem Netzwerk verbunden werden.
Dabei bezeichnet man die Eckpunkte als Knoten und die Verbindungen als Kanten des Netzwerks.
Die Länge des Netzwerks ist die Summe der Kantenlängen, die in diesem Rätsel immer minimal werden soll. Es sind also keine Diagonalen der Flächen oder des Raums zu wählen sondern nur Kanten zu den nächsten Nachbarpunkten.
Nebenstehend ist eine von vielen Möglichkeiten mit gelben Netzwerkkanten dargestellt.
Die Länge des Netzwerks ohne zusätzliche Knoten ist dann $$\rand{ L_0=7\cdot Kantenlänge=14 }$$
3.) Netzwerk mit einem zusätzlichen Knoten
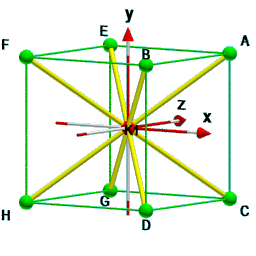Wegen der Symmetrie bietet sich nur eine Position für einen zusätzlichen Knoten an: $K_1=(0,0,0)$.
Das nebenstehende Bild zeigt diese Situation.
Alle acht Eckpunkte sind mit diesem Knoten direkt verbunden.
Die Länge der einzelnen Verbindungen entspricht der Hälfte der Raumdiagonale des Würfels:
$$Raumdiagonale=\sqrt{3\cdot Kantenlänge^2}=2\cdot\sqrt{3}=3,46410162$$
Also ergibt sich für die Länge des Netzwerks
$$\rand{
L_1={\textstyle\frac82}\cdot Raumdiagonale=8\cdot\sqrt{3}=13,85640646}$$
Somit ist das Netzwerk $L_1$ etwas kürzer als das Netzwerk $L_0$.
4.) Netzwerk mit zwei zusätzlichen Knoten
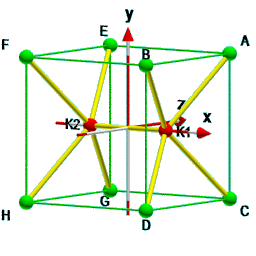Wie aus nebenstehendem Bild zu sehen ist, liegen die beiden zusätzlichen Knoten auf einer Koordinatenachse,
in diesem Beispiel auf der x-Achse, gleich weit vom Ursprung entfernt.
Die einzige Unbekannte ist also dieser Abstand als x-Koordinate, einmal positiv und einmal negativ für die beiden Knoten.
Die übrigen Koordinaten sind Null.
Also gilt
$$\begin{align}
K_1&=(x,0,0)&K_2&=(-x,0,0)
\end{align}$$
Das Netzwerk besteht also aus der Kante $\overline{K_1K_2}=2x$
und acht mal die Länge der Kante $\overline{K_1A}=\sqrt{(1-x)^2+2}$.
Die Länge des Netzes mit zwei zusätzlichen Knoten als Funktion von $x$ ist also
$$
y(x)=2x+8\cdot\sqrt{(1-x)^2+2}\tag{1}
$$
Zur Berechnung des Minimums wird die Ableitung berechnet:
$$
y'(x)=2-\frac{8\cdot(1-x)}{\sqrt{(1-x)^2+2}}\tag{2}
$$
Wenn man nun $y'$ in (2) gleich Null setzt, bekommt man eine Bestimmungsgleichung für $x$:
$$\begin{align}
\sqrt{(1-x)^2+2}&=4\cdot(1-x) \\
(1-x)^2+2&=16\cdot(1-x)^2 \\
15\cdot(1-x)^2&=2 \\
x&=1-\sqrt{{\textstyle\frac2{15}}}=0,63485163\end{align}$$
und $x$ eingesetzt in (1) ergibt für die Länge des Netzes mit zwei zusätzlichen Knoten
$$\rand{
L_2=\sqrt{30}\cdot 2+2=12,95445115}$$
5.) Netzwerk mit fünf zusätzlichen Knoten
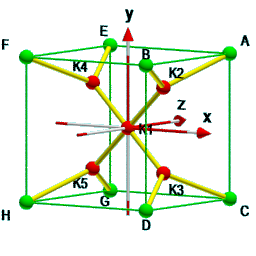Das nebenstehende Bild zeigt im Zentrum ein Kreuz, welches um 45° gegen die xy-Achsen gedreht ist.
Daraus folgt, dass die unbekannte x-Koordinate der Knoten $K_{2,3,4,5}$ betragsmäßig mit der y-Koordinate gleich ist.
Also gilt
$$\begin{align}
K_2&=(x,x,0)&K_3&=(-x,x,0) \\
K_4&=(x,-x,0)&K_5&=(-x,-x,0)
\end{align}$$
Das Netzwerk besteht also aus vier mal der Kante $\overline{K_1K_2}=4\sqrt2x$
und acht mal die Länge der Kante $\overline{K_2A}=\sqrt{2(1-x)^2+1}$.
Die Länge des Netzes mit fünf zusätzlichen Knoten als Funktion von $x$ ist also
$$
y(x)=4\sqrt2x+8\sqrt{2(1-x)^2+1}\tag{3}
$$
Zur Berechnung des Minimums wird die Ableitung berechnet:
$$
y'(x)=4\sqrt2-\frac{16(1-x)}{\sqrt{2(1-x)^2+1}}\tag{4}
$$
Wenn man nun $y'$ in (4) gleich Null setzt, bekommt man eine Bestimmungsgleichung für $x$:
$$
\sqrt2=\frac{4(1-x)}{\sqrt{2(1-x)^2+1}} \\
\sqrt{4(1-x)^2+2}=4(1-x) \\
4(1-x)^2+2=16(1-x)^2 \\
6(1-x)^2=1 \\
x=1-{\textstyle\frac16}\cdot\sqrt{6}=0,59175171$$
und $x$ eingesetzt in (3) ergibt für die Länge des Netzes mit fünf zusätzlichen Knoten
$$\rand{
L_5=4\cdot(\sqrt{2}+\sqrt{3})=12,58505748}$$
6.) Netzwerk mit sechs zusätzlichen Knoten
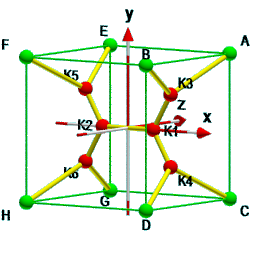
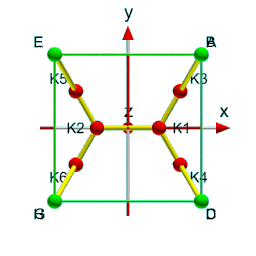
Damit man die Winkel besser erkennt, ist links unten eine andere Perspektive gewählt. Hier liegen alle sechs Knoten in der Bildschirmebene, also reicht es, alle Berechnungen in der xy-Ebene durchzuführen. Man kann sich zudem auf den ersten Quadranten ($x,y\ge0$) beschränken, denn die anderen Punkte sind Spiegelbilder.
Rechts unten ist eine Zeichnung dieses ersten Quadranten mit Punktbezeichnungen und Winkel. Folgende Strecken werden hier definiert:
| $$\overline{ZK_1}=x_1 \\ \overline{WK_3}=x_3 \\ \overline{ZW}=y_3 \\ \overline{K_1B}=d \\ \overline{K_3B}=h \\ \overline{K_1X}=1-x_1 \\ \overline{ZX}=\overline{ZY}=1$$ |
Die gesuchten Koordinaten der beiden Knoten sind dann $K_1=(x_1,0,0)$ und $K_3=(x_3,y_3,0)$. Die Strecke $h$ ist die Höhe des Dreiecks $\triangle ABK_3$, welches nur in der oberen linken Darstellung zu sehen ist. Dieses Dreieck hat ebenfalls einen Winkel von 120° am Knoten $K_3$. Da der Abstand $\overline{AB}=2$ ist, ist die gesuchte Höhe $h=\tan(30°)={\textstyle\frac13}\sqrt3$. Ebenfalls ist die Strecke $1-x_1=\tan(30°)={\textstyle\frac13}\sqrt3$ und die Strecke $d$ ist doppelt so groß wegen $\sin(30°)={\textstyle\frac12}$. Also liegt der Knoten $K_3$ in der Mitte von $d$. Daraus lassen sich nun alle noch unbekannten Strecken bestimmen: $$ x_1=1-{\textstyle\frac13}\sqrt3=0,42264973 \\ x_3=1-{\textstyle\frac16}\sqrt3=0,71132487 \\ y_3={\textstyle\frac12}=0,50000000$$ Die Länge des Netzwerks ist dann $$ L_6=2\cdot x_1+4\cdot h+8\cdot 2h \\ L_6=2-{\textstyle\frac23}\sqrt3+{\textstyle\frac43}\sqrt3+{\textstyle\frac{16}3}\sqrt3 \\ $$ $$\rand{ L_6=\sqrt{3}\cdot 6+2=12,39230485}$$
7.) Zusammenfassung
| zus. Knoten | Koordinaten | Netzwerklänge | |
|---|---|---|---|
| 0 | - | $7\cdot2$ | $14,00000000$ |
| 1 | $K_1=(0,0,0)$ | $8\cdot\sqrt3$ | $13,85640646$ |
| 2 | $x=1-{\textstyle\frac1{15}}\sqrt{30}=0,63485163$
$K_{1,2}=(\pm x,0,0)$ |
$\sqrt{30}\cdot 2+2$ | $12,95445115$ |
| 5 | $x=y=1-{\textstyle\frac16}\sqrt{6}=0,59175171$
$K_1=(0,0,0)$ $K_{2,3,4,5}=(\pm x,\pm y,0)$ |
$4\cdot(\sqrt{2}+\sqrt{3})$ | $12,58505748$ |
| 6 | $x_1=1-{\textstyle\frac13}\sqrt3=0,42264973$
$x_3=1-{\textstyle\frac16}\sqrt3=0,71132487$ $y_3={\textstyle\frac12}=0,50000000$ $K_{1,2}=(\pm x_1,0,0)$ $K_{3,4,5,6}=(\pm x_3,\pm y_3,0)$ |
$\sqrt{3}\cdot 6+2$ | $12,39230485$ |
8.) alternative Lösungen
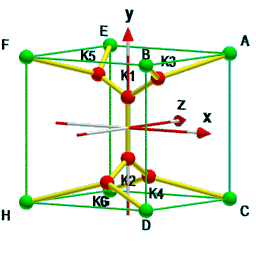In den obigen Lösungen sind alle zusätzliche Knoten in einer Ebene mit der z-Koordinate Null angesiedelt.
Das muss natürlich nicht so sein, wie nebenstehendes Bild veranschaulicht.
Die Knoten $K_1$ und $K_2$ sind von der x-Achse zur y-Achse gewechselt
und die Knoten $K_4$ und $K_6$ sind gegenüber dem Knotenpaar $K_{3,5}$ um die y-Achse um 90° gedreht.
Es sind auch alle weiteren Tauschmöglichkeiten zwischen den Koordinaten ebenfalls Lösungen. Das ändert aber weder an der minimalen Länge des Netzwerks etwas, noch an den Zahlenwerten der Koordinaten.