Lösungsbeschreibung des Preisrätsels vom Juni 2014

Standfuß für eine Kugel


1.) Schnittbild und Grundriss


Das obige Bild zeigt einen senkrechten Schnitt durch Standfuß und aufliegender Kugel. Dabei zeigt die Schnittfläche, wie die Kugel in der Mitte den Boden berührt. Der sternförmige Standfuß wird so angeschnitten, dass rechts bei maximaler Höhe eine der Spitzen durchteilt wird (in der unteren Zeichnung des Grundrisses die obere Spitze) und links die minimale Höhe des Randes erreicht wird (in der Zeichnung zwischen den Spitzen unten).

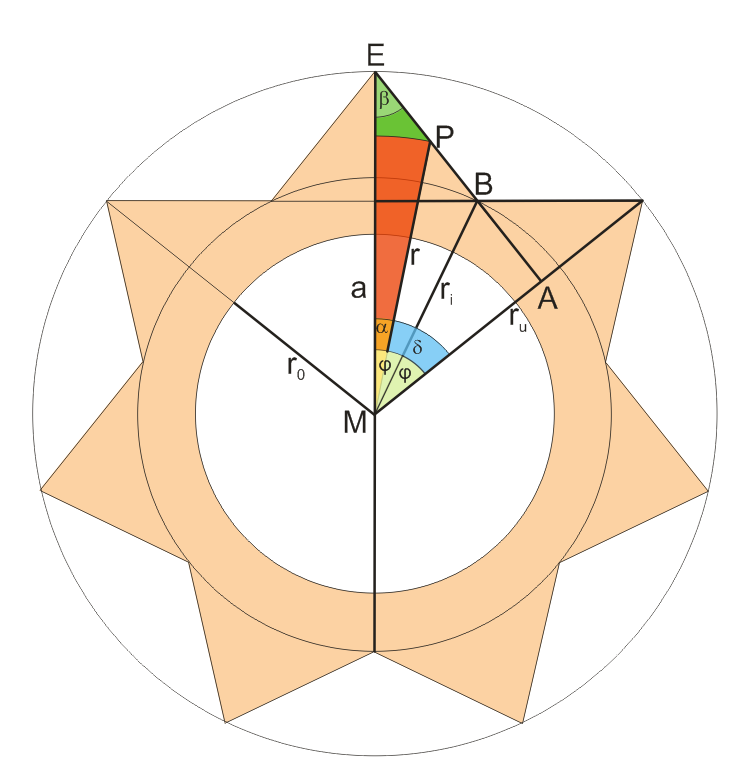
2.) Definitionen und Zusammenhänge

Mit Hilfe der Eigenschaften des 7/2-Sterns kann aus dem Umkreisradius $r_u$ der Inkreisradius $r_i$ des runden Zentralkörpers ohne Spitzen berechnet werden. $$\text{aus}\quad\sand{a=r_u\cdot\cos 2\varphi} \quad\text{und}\quad \sand{a=r_i\cdot\cos\varphi}\quad\text{folgt}$$ $$\sand{r_i=r_u\cdot\frac{\cos 2\varphi}{\cos\varphi}} \quad\text{mit}\quad \sand{\varphi=\frac{2\pi}{14}} \quad\text{dem Winkel zwischen}\quad r_i\quad\text{und}\quad r_u$$ $$\text{Der Radius $r_0$ der zentralen Bohrung ist}\quad\sand{r_0=0,500000000000\cdot r_u}$$ $$\text{Der Radius $r_k$ der Glaskugel ist}\quad\sand{r_k=1,200000000000\cdot r_u}$$ Der Winkel $\beta$ ist konstant für alle Dreiecke $\triangle MEP$, Auch wenn der Punkt $P$ andere Positionen auf der Strecke $\overline{BE}$ einnimmt. $$\sand{\beta=\frac{\pi}2-2\varphi=\frac{3\pi}{14}}$$ Die grüne Teilfläche des Dreiecks $\triangle MEP$ ist der Repräsentant aller horizontalen Schnittebenen durch das zu bestimmende Volumensegment, welches der 14. Teil des Standfußes ist (grünes Volumenelement in der Darstellung unten).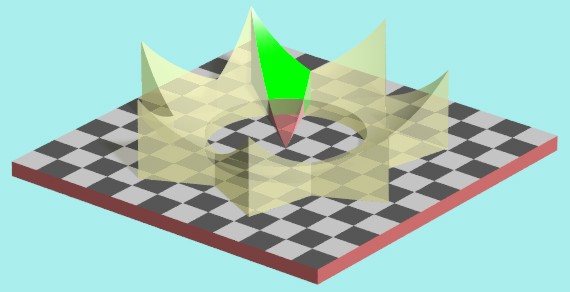

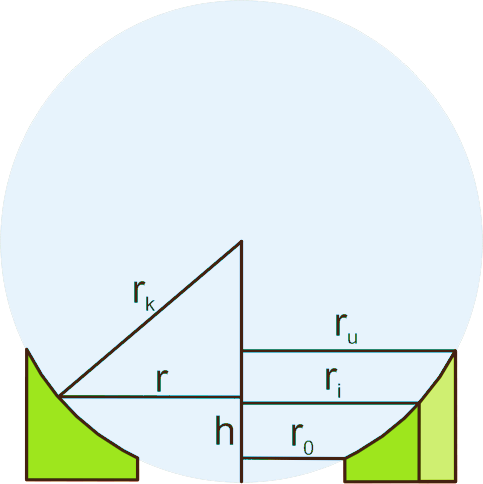
Die Fläche der Schnittebene durch das gesuchte Volumenelement lässt sich als Differenz des Dreiecks $\triangle MEP$ und des Kreisausschnitts mit Öffnungswinkel $\alpha$ angeben. $$\sand{F_{grün}\left(r_d,r_a,\alpha\right)=F_{Dreieck}-F_{Kreisausschnitt}=r_u\cdot r_d\cdot\frac{\sin\alpha}2-{r_a}^2\pi\cdot\frac\alpha{2\pi}}$$ Die Fläche ändert sich in Abhängigkeit von $r_d$, $r_a$ (in der Zeichnung oben mit $r$ bezeichnet) und $\alpha$ und damit von der Höhe der Schnittebene. Dabei ist der Radius $r_d$ zum Dreieck und der Radius $r_a$ zum Kreisausschnitt zuzuordnen, was für Höhen mit Radien unter $r_i$ nicht identisch ist. Der Punkt $P$ liegt bei Radien $r_a < r_i$ fest auf B und läuft dann auf der Strecke $\overline{BE}$ zum Punkt $E$, während der Radius $r_d$ von $r_i$ nach $r_u$ steigt. Der Zusammenhang von Höhe $h$ und $r$ ergibt sich aus $$\sand{\left(r_k-h\right)^2+r^2={r_k}^2} \quad\text{oder}\quad \sand{r^2=2h\cdot r_k-h^2}$$ mit $r_k$ als Radius der Glaskugel, die in der Mitte den Boden berührt (siehe folgende Zeichnung).


Die Höhen, die zu den Radien $r_0$, $r_i$ und $r_u$ gehören sind $$\sand{h_0=r_k-\sqrt{{r_k}^2-{r_0}^2}}\quad\sand{h_i=r_k-\sqrt{{r_k}^2-{r_i}^2}}\quad\sand{h_u=r_k-\sqrt{{r_k}^2-{r_u}^2}}$$ Das nun noch fehlende Element ist der Winkel $\alpha$, der in die Flächenberechnung eingeht und der sich bei $r>r_i$ in Abhängigkeit vor $r$ verändert. Die einfachste von mir gefundene Darstellung ist $$\sand{\alpha=2\varphi-\arccos\frac ar}$$

3.) Berechnung mit Integralen

Da bei der Rätselfrage nur nach dem Verhältnis der Volumina gefragt wurde, ist eine absolute Größe der Abmessungen nicht erforderlich. Deshalb lege ich für die unten folgenden numerischen Berechnungen der Integrale den Radius des Umkreises $r_u$ des (7/2)-Sterns als Bezugsgröße für alle anderen Abmessungen fest und gebe ihm den Wert 1.

Es sind für verschiedene Höhen unterschiedliche funktionale Zusammenhänge festzulegen (Fallunterscheidung).

Fall Höhenbereich $r_d$ $r_a$ $\alpha$
von bis
III$h_i$$h_u$$\sqrt{2h\cdot r_k-h^2}$$2\varphi-\arccos\frac a{r_a}$
II$h_0$$h_i$$r_i$$\sqrt{2h\cdot r_k-h^2}$$\varphi$
I$0$$h_0$$r_i$$r_0$$\varphi$

Nun kann man alles zusammenfassen. Das Volumen des Standfußes ist: $$\sand{V_{Standfuß}=14\cdot\left(\intop_0^{h_0}F_{I}(h)dh+\intop_{h_0}^{h_i}F_{II}(h)dh+\intop_{h_{i}}^{h_u}F_{III}(h)dh\right)}$$
Fall I: $$\sand{V_I=\intop_0^{h_0}F_{I}(h)dh=\intop_0^{h_0}\left(r_u\cdot r_i\cdot\frac{\sin\varphi}2-{r_0}^2\cdot\frac\varphi2\right)dh= 0,010261223170}$$
 
Fall II: $$\sand{V_{II}=\intop_{h_0}^{h_i}F_{II}(h)dh=\intop_{h_0}^{h_i}\left(r_u\cdot r_i\cdot\frac{\sin\varphi}2-(2r_kh-h^2)\cdot\frac\varphi2\right)dh}$$ $$\sand{V_{II}=\intop_{h_0}^{h_i}\frac{r_u r_i\sin\varphi}2-\frac\varphi2\cdot\intop_{h_0}^{h_i}(2r_kh-h^2)\;dh}$$ $$\sand{V_{II}=\left[\frac{r_u r_i\sin\varphi}2\cdot h-\frac\varphi2\cdot\left(r_kh^2-\frac{h^3}3\right)\right]_{h_0}^{h_i}= 0,007502586481}$$
 
Fall III: $$\sand{V_{III}=\intop_{h_{i}}^{h_u}F_{III}(h)dh=\intop_{h_i}^{h_u}\left(r_u\cdot r_d\cdot\frac{\sin\alpha}2-{r_a}^2\cdot\frac\alpha2\right)dh}$$ $$\sand{V_{III}=\intop_{h_i}^{h_u}\tona{r_u\cdot r_d\cdot\frac{\sin\alpha}2}dh-\intop_{h_i}^{h_u}{r_a}^2\cdot\frac\alpha2dh}$$ $$\sand{\alpha=2\varphi-\delta}\quad\sand{cos\delta=\frac a{r_d}}\quad\sand{sin\delta=\sqrt{1-\left(\frac a{r_d}\right)^2}}$$ $$\sand{\sin\alpha=\sin(2\varphi-\delta)=\sin2\varphi\cdot\cos\delta-\cos2\varphi\cdot\sin\delta}$$ $$\sand{\sin\alpha=\sin2\varphi\cdot\frac a{r_d}-\cos2\varphi\cdot\sqrt{1-\left(\frac a{r_d}\right)^2}}$$ $$\sand{\tona{\frac{r_ur_d}2\cdot\sin\alpha}=\sin2\varphi\cdot\frac{r_ua}2-\frac a2\cdot\sqrt{{r_d}^2-a^2}}$$ $$\sand{V_{III}=\sin2\varphi\cdot\frac{r_ua}2\cdot\intop_{h_i}^{h_u}1\;dh -\frac a2\cdot\intop_{h_i}^{h_u}{\sqrt{{r_d}^2-a^2}}dh -\intop_{h_i}^{h_u}{r_a}^2\cdot\frac\alpha2dh}$$ $$\sand{V_{III}=\tond{\left[\sin2\varphi\cdot\frac{r_uah}2\right]_{h_i}^{h_u}} -\tonc{\frac a2\cdot\intop_{h_i}^{h_u}{\sqrt{{r_d}^2-a^2}}dh} -\tonb{\intop_{h_i}^{h_u}{r_a}^2\cdot\frac\alpha2dh}}$$ $$\sand{V_{IIIa}=\tond{\left[\sin2\varphi\cdot\frac{r_uah}2\right]_{h_i}^{h_u}}= 0,077271646646}$$ $$\sand{\begin{array}{ccc}V_{IIIb}=\tonc{\frac a2\cdot\intop_{h_i}^{h_u}{\sqrt{{r_d}^2-a^2}}dh}=\frac a2\cdot\intop_{h_i}^{h_u}\sqrt{2r_kh-h^2-a^2}dh \\ =\frac a2\cdot\left[\left(\frac{h-r_k}2\right)\cdot\sqrt{2r_kh-h^2-a^2} \\ -\frac12\left({r_k}^2-a^2\right)\cdot\arctan\frac{(r_k-h)}{\sqrt{2r_kh-h^2-a^2}}\right]_{h_i}^{h_u}= 0,058450242271\end{array}}$$ $$\sand{\begin{array}{ccccc}V_{IIIc}=\tonb{\intop_{h_i}^{h_u}{r_a}^2\cdot\frac\alpha2dh}=\frac12\cdot\intop_{h_i}^{h_u}(2r_kh-h^2)\cdot\left(2\varphi-\arccos\frac{a}{\sqrt{2r_kh-h^2}}\right)dh \\ =\frac12\left[2r_kh^2\cdot\varphi-\frac{2\varphi}3\cdot h^3+\frac{a(h-r_k)}6\cdot\sqrt{2r_kh-h^2-a^2} \\ +\left(\frac{h^3}3-r_kh^2\right)\cdot\arccos\frac a{\sqrt{2r_kh - h^2}} \\ -\frac a6(a^2+3{r_k}^2)\cdot\arctan\left((r_k-h)\cdot\sqrt{2r_kh-h^2-a^2}\right) \\ -\frac23{r_k}^3\cdot\arctan\frac{a\cdot\sqrt{2r_kh-h^2-a^2}}{2{r_k}^2-a^2-r_kh}\right]_{h_i}^{h_u}= 0.015288440691447\end{array}}$$ $$\sand{V_{III}=V_{IIIa}-V_{IIIb}-V_{IIIc}= 0,003532963684}$$

Insbesondere für den letzten Teil ($V_{III}$) war sowohl die numerische als auch die allgemeine Lösung von "Wolfram Mathematica Online Integrator" sehr hilfreich. Man hat trotzdem noch genug zu tun, um die angezeigten Lösungen aufzubereiten.
Nun kommen wir ans baldige Ende der Rechnung. Zusammen ergibt sich für das Volumen des Standfußes $$\sand{V_{Standfuß}=14\cdot\left(V_I+V_{II}+V_{III}\right)=0,298154826688}$$ Das Volumen der Glaskugel ist $$\sand{V_{Glaskugel}=\frac43\cdot\pi {r_k}^3=7,238229473871}$$ Also ist abschließend die Rätselfrage nach dem Verhältnis der Volumina von Kugel zu Standfuß zu beantworten mit $$\rand{\frac{V_{Glaskugel}}{V_{Standfuß}}=24,276747602147}$$ Die obige numerische Berechnung der Integrale erfolgt live serverseitig. Dadurch ist es auch möglich, mit anderen Startwerten die Berechnung durchzuführen. Wenn man z.B. die zentrale Bohrung weglassen möchte setzt man den Wert von $r0$ auf Null. Das geht durch Parameterübergabe in der Adresszeile. Man hängt an die oben im Browser stehende Internetadresse dieser Seite noch ?r0=0 an und macht einen Bildneuaufbau, indem die Seite neu geladen wird. Es ändern sich alle entsprechenden Zahlenwerte in den gelben Feldern. Der eingegebene Zahlenwert für den Parameter wird als Vielfaches von $r_u$ aufgefasst. Genauso kann auch der Radius der Glaskugel $r_k$ geändert werden. Dazu wäre z.B. ?rk=1.5 anzuhängen. Will man mehrere Parameter gleichzeitig ändern, so wäre beispielsweise ?r0=0&rk=1.5 anzuhängen. Auch $r_u$ kann geändert werden. Damit wird aber nur eine Größenveränderung erreicht, das Verhältnis bleibt das gleiche wie ohne diese Veränderung: z.B. ?ru=2. Bei unsinnigen Werten (zu kleine Glaskugel oder negative Werte) gibt es unsinnige Ergebnisse oder Fehlermeldungen. Bilder werden nicht verändert.

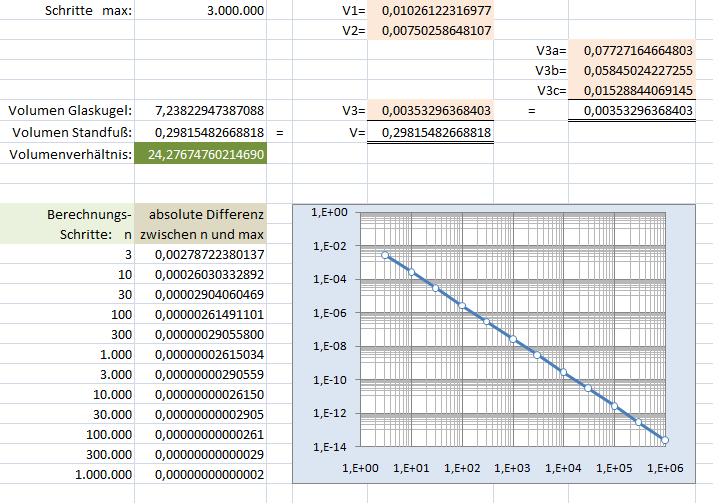
4.) Berechnung mit EXCEL

Wenn man mal schnell einen Überblick über ein Problem benötigt, ist EXCEL das richtige Werkzeug. Auch für dieses Rätsel lag schnell ein Ergebnis vor. Natürlich müssen die gleichen Überlegungen angestellt werden, wie oben beschrieben. Aber der Weg der numerischen Integration ist wesentlich einfacher und schneller zu bewerkstelligen. Statt wie beim Integral einen Grenzwertübergang nach unendlich zu machen und oft mühsam nach der richtigen Stammfunktion zu suchen bleibt man bei endlichen Schrittzahlen und dem einfacheren funktionalen Zusammenhang. Da der Rechner sehr schnell ist sind Schrittzahlen von Millionen zur Erzielung hoher Genauigkeit kein Problem. Durch die vorangegangene Aufarbeitung sind keine weiteren Erklärungen für das Programm nötig. Die benutzten Variablen haben im Wesentlichen gleiche Namen.
Hier soll noch der Hinweis erfolgen, dass nicht immer alle benötigten Funktionen eingebaut sind. In diesem Beispiel fehlte die Funktion "arcuscosinus". Deshalb ist unterhalb der Funktion "Vstandfuss" noch die Funktion "Arccos" angefügt.
Ich benutzte die maximale Schrittzahl 3.000.000 für die numerische Integration. Das VISUAL BASIC Programm ist auch auf die Berechnung der Zwischenergebnisse ausgelegt, um auf einem zweiten Weg die Ergebnisse der Integrale zu überprüfen. Es ist daher länger als für die Berechnung des Volumens des Standfußes erforderlich. Zum Nachempfinden kann der folgende Text kopiert und in ein zu erzeugendes Modul im EXCEL-Fenster "VISUAL BASIC" eingefügt werden. Auf den Tabellenblättern steht anschließend die so definierte Funktion wie jede schon eingebaute zur Verwendung bereit, natürlich mit Eingabemöglichkeit für die Parameter. Wer es noch einfacher haben will kann hier das fertige EXCEL-Programm herunterladen. Nicht vergessen: bei der Sicherheitseinstellung das Makro freigeben!
Der 1. Parameter ist die Schrittzahl. Mit steigender Zahl dauert die Rechnung länger, und da auf dem Demo-Tabellenblatt 7 mal der Funktionsaufruf mit unterschiedlichen Parametern erfolgt, kann das schon je nach Rechnerleistung viele Sekunden, sogar Minuten dauern.
Der 2. Parameter betrifft die Auswahl: Der 3. Parameter ist optional und macht nur Sinn bei Fall III und bedeutet: 

Function Vstandfuss(schritte, teil, Optional area = 0)

    Pi = 4 * Atn(1)
    phi = 2 * Pi / 14
    beta = Pi / 2 - 2 * phi

    Ru = 1: Rk = 1.2: R0 = 0.5
    Ri = Ru * Cos(2 * phi) / Cos(phi)

    a = Ru * Sin(beta)
    Dim V(3)
    h0 = Rk - Sqr(Rk * Rk - R0 * R0)
    hi = Rk - Sqr(Rk * Rk - Ri * Ri)
    hu = Rk - Sqr(Rk * Rk - Ru * Ru)

    Fd = Ru * Ri * Sin(phi) / 2
    Fk = R0 * R0 * phi / 2
    V(1) = (Fd - Fk) * h0

    dh = (hi - h0) / schritte
    V(2) = 0
    For i = 1 To schritte
        h = h0 + i * dh - dh / 2
        r = Sqr(2 * h * Rk - h * h)
        Fd = Ru * Ri * Sin(phi) / 2
        Fk = r * r * phi / 2
        V(2) = V(2) + (Fd - Fk) * dh
    Next i

    dh = (hu - hi) / schritte
    V(3) = 0
    For i = 1 To schritte
        h = hi + i * dh - dh / 2
        r = Sqr(2 * h * Rk - h * h)
        alpha = 2 * phi - Arccos(a / r)
        Fd = Ru * r * Sin(alpha) / 2
        Fk = r * r * alpha / 2

        Select Case area
            Case 0
                F = Fd - Fk
            Case "a"
                F = Sin(2 * phi) * Ru * a / 2
            Case "b"
                F = Fd
            Case "c"
                F = Fk
        End Select

        V(3) = V(3) + F * dh
    Next i

    If teil = 0 Then
        Vstandfuss = (V(1) + V(2) + V(3)) * 14
    Else
        Vstandfuss = V(teil)
    End If

End Function

Function Arccos(w)
    Arccos = Atn(-w / Sqr(-w * w + 1)) + 2 * Atn(1)
End Function

Hier folgt nun die Ansicht des EXCEL Tabellenblatts mit verschiedenen Ergebnissen. Wer experimentieren will und keinen superschnellen Rechner hat, kann auf eine Dezimalstelle in der Genauigkeit verzichten und die Schrittzahl um den Faktor 100 heruntersetzen. Damit läuft der Rechner 100 mal schneller. Der Zusammenhang von Genauigkeit und Schrittzahl geht auch aus dem Diagramm hervor, welches mit unterschiedlichen Schrittzahlen auf dem Tabellenblatt erzeugt wurde. Um aber den Rechner nicht immer wieder mit dieser Rechnung zu belasten sind die Ergebnisse als Wert in die Tabelle eingetragen.



Diese Informationen wurden zusammengestellt von

Kurzbewertung dieser Information:
sehr gut gut befriedigend
ausreichend mangelhaft ungenügend