Lösungsbeschreibung des Preisrätsels vom Juni 2019

Das zerteilte Dreieck

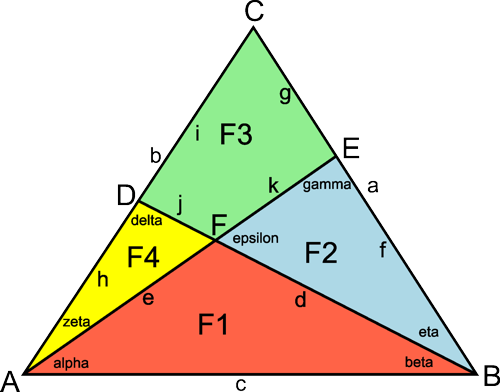
1.) Berechnungsschritte

Wenn man von gegebenen Werten für $\alpha$ und $\beta$ ausgeht, sind die restlichen Winkel in der obigen Zeichnung eines gleichseitigen Dreiecks nach folgenden Gleichungen zu berechnen: $$\begin{align} \alpha\, (alpha) & = gegeben \\ \beta\, (beta) & = gegeben \\ \gamma\, (gamma) & = 120°-\alpha \\ \delta \, (delta) & = 120 - \beta \\ \epsilon \, (epsilon) & = \alpha + \beta \\ \zeta\, (zeta) & = 60°-\alpha \\ \eta\, (eta) & = 60°-\beta \\ \end{align}$$ Da keine absoluten Abmessungen der Strecken für dieses Rätsel gebraucht werden, kann eine beliebige Festlegung erfolgen. Für die spätere numerische Berechnung werden die drei Seiten des gleichseitigen Dreiecks auf die Länge 1 normiert: $$ a=b=c=1 $$ Die einzelnen Teilstrecken können für jedes Teildreieck berechnet werden nach dem Sinussatz: $$\sand{ \frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma} }$$ $$\begin{align} d & = c \cdot \frac{\sin\alpha}{\sin\epsilon} & \quad\quad\quad e & = c \cdot \frac{\sin\beta}{\sin\epsilon} \\ f & = c \cdot \frac{\sin\alpha}{\sin\gamma} & \quad\quad\quad g & = a - f \\ h & = c \cdot \frac{\sin\beta}{\sin\delta} & \quad\quad\quad i & = a - h \\ j & = e \cdot \frac{\sin\zeta}{\sin\delta} & \quad\quad\quad k & = d \cdot \frac{\sin\eta}{\sin\gamma} \\ \end{align}$$ Die Flächen von allgemeinen Dreiecken können nach folgender Formel aus deren Seiten berechnet werden: $$\sand{ F_{\Delta}=\sqrt{s\cdot(s-a)\cdot(s-b)\cdot(s-c)}\quad\text{mit}\quad s=\frac{a+b+c}{2} }$$ Das ergibt für die vier Teilflächen des gleichseitigen Dreiecks: $$ F1=\sqrt{s1\cdot(s1-c)\cdot(s1-d)\cdot(s1-e)}\quad\text{mit}\quad s1=\frac{c+d+e}{2} \\ F2=\sqrt{s2\cdot(s2-d)\cdot(s2-f)\cdot(s2-k)}\quad\text{mit}\quad s2=\frac{d+f+k}{2} \\ F4=\sqrt{s4\cdot(s4-e)\cdot(s4-j)\cdot(s4-h)}\quad\text{mit}\quad s4=\frac{e+j+h}{2} \\ F3=\frac{a^2}{4}\cdot\sqrt{3}-F1-F2-F4 $$ Mit den obigen Formeln lassen sich die Teilflächen als Funktion von $\alpha$ und $\beta$ berechnen.

2.) Flächengleichheit

Aus der Forderung, dass Teilflächen gleich groß sein sollen, kann man folgendes ableiten:

• Wenn $F1=F3$ dann auch die Dreiecke $F1+F2=F2+F3$. Diese Dreiecke haben dann nicht nur die gleiche Fläche, sondern auch eine gleichlange Seite c bzw. a und einen gleichen Winkel von 60° bei B bzw. C. Daraus folgt, dass sie deckungsgleich sein müssen und die Winkel $\alpha$ und $\eta$ sind gleich. Der Schnittpunkt $F$ liegt auf dem grauen Kreisbogen (Bild unten).
  Das bedeutet: $$ \text{wenn }\; F1 = F3 \;\text{ dann }\; \alpha + \beta=60°\;\text{und umgekehrt} $$
• Wenn $F2=F4$ dann auch die Dreiecke $F1+F2=F1+F4$ Diese Dreiecke haben dann nicht nur die gleiche Fläche, sondern auch eine gleichlange Seite c und einen gleichen Winkel von 60° bei B bzw. A. Daraus folgt, dass sie deckungsgleich sein müssen und die Winkel $\alpha$ und $\beta$ sind gleich. Der Schnittpunkt $F$ liegt auf der weißen Geraden (Bild unten).
  Das bedeutet: $$ \text{wenn }\; F2 = F4 \;\text{ dann }\; \alpha = \beta\;\text{und umgekehrt} $$

Beide Forderungen zusammen ergeben $\alpha = \beta = 30°$. Der Schnittpunkt $F$ liegt auf dem Schnittpunkt der weißen Geraden und dem grauen Kreisbogen (Bild unten). Die Berechnung der Flächen (siehe Ergebnistabelle unten) ergibt $$F1 = F3\ne F2 = F4$$ Deshalb können nicht alle vier Teilflächen gleich groß werden.

3.) Flächengleichheit bei drei Teilflächen

Wie man die Gleichheit der Flächen $F1$ und $F3$ herstellt, wurde gerade oben beschrieben. Wenn man nun $\alpha$ von 0° bis 60° variiert und dabei $\beta=60°-\alpha$ setzt, kann man sich die beiden Funktionen $F1(\alpha)-F2(\alpha)$ und $F1(\alpha)-F4(\alpha)$ ansehen und deren Nullstellen suchen. Auf diese Weise sucht man zu den gleichen Flächen $F1$ und $F3$ noch eine dritte gleichgroße Fläche, zum einen $F2$ und zu anderen $F4$.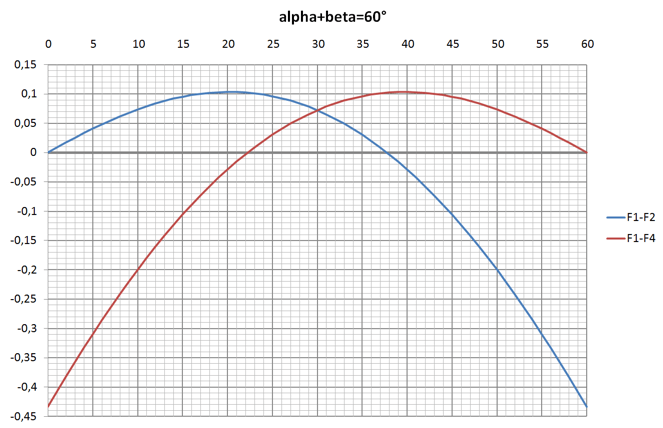


Man sieht, dass bei $\alpha≈22°$ die drei Flächen $F1\;F3\;F4$ gleich sind (Nulldurchgang der roten Kurve).
Für $\alpha≈38°$ sind die Flächen $F1\;F2\;F3$ gleich (Nulldurchgang der blauen Kurve).
Die genauen Werte können mit eine Intervallschachtelung oder dem Newton-Näherungsverfahren bestimmt werden.


Genauso geht man vor, wenn mit $\alpha=\beta$ die Flächen $F2$ und $F4$ gleichgemacht werden und $\alpha$ auch hier von 0° bis 60° variiert wird. Dabei betrachtet man die Funktionen $F2(\alpha)-F1(\alpha)$ und $F2(\alpha)-F3(\alpha)$.


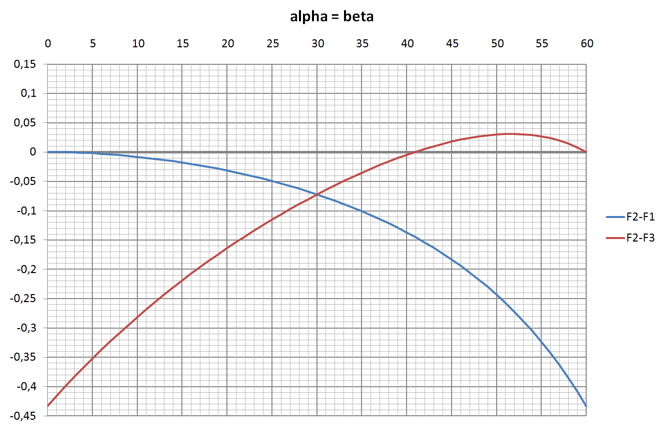Die blaue Kurve hat keine Nullstelle (außer bei $\alpha=0°$ und das ist kein Schnitt). Die rote Kurve zeigt, dass für $\alpha≈41°$ die Flächen $F2\;F3\;F4$ gleich sind. Auch hier kann mit Intervallschachtelung der genaue Wert eingegrenzt werden.

4.) Ergebnistabelle

Variable	keine Lösung F1=F3 ≠ F2=F4	Lösung 1 F1=F3=F4 ≠ F2	Lösung 2 F1=F2=F3 ≠ F4	Lösung 3 F1 ≠ F2=F3=F4
α	30,000000000000	22,238756092965	37,761243907035	40,893394649131
β	30,000000000000	37,761243907035	22,238756092965	40,893394649131
γ	90,000000000000	97,761243907035	82,238756092965	79,106605350869
δ	90,000000000000	82,238756092965	97,761243907035	79,106605350869
ϵ	60,000000000000	60,000000000000	60,000000000000	81,786789298262
ζ	30,000000000000	37,761243907035	22,238756092965	19,106605350869
η	30,000000000000	22,238756092965	37,761243907035	19,106605350869
a	1,000000000000	1,000000000000	1,000000000000	1,000000000000
b	1,000000000000	1,000000000000	1,000000000000	1,000000000000
c	1,000000000000	1,000000000000	1,000000000000	1,000000000000
d	0,577350269190	0,437016024449	0,707106781187	0,661437827766
e	0,577350269190	0,707106781187	0,437016024449	0,661437827766
f	0,500000000000	0,381966011250	0,618033988750	0,666666666667
g	0,500000000000	0,618033988750	0,381966011250	0,333333333333
h	0,500000000000	0,618033988750	0,381966011250	0,666666666667
i	0,500000000000	0,381966011250	0,618033988750	0,333333333333
j	0,288675134595	0,437016024449	0,166925267711	0,220479275922
k	0,288675134595	0,166925267711	0,437016024449	0,220479275922
F1	0,144337567297	0,133808283665	0,133808283665	0,216506350946
F2	0,072168783649	0,031587850897	0,133808283665	0,072168783649
F3	0,144337567297	0,133808283665	0,133808283665	0,072168783649
F4	0,072168783649	0,133808283665	0,031587850897	0,072168783649

5.) alternative Lösungsbeschreibung

Bemerkenswert ist der Umstand, dass bei Lösung 1 und 2 die Schnitte durch die Seiten a und b diese im Verhältnis des goldenen Schnitts teilen. Bei Lösung 3 ist die Teilung 2 zu 1.

Deshalb kann man die Lösung dieses Rätsels auch so beschreiben:

Winkel	Lösung 1	Lösung 2	Lösung 3
$α$	$\arctan((\sqrt{5}-2)\cdot\sqrt{3})$	$\arctan(\frac15\cdot\sqrt{5}\cdot\sqrt{3})$	$\arctan(\frac12\cdot\sqrt{3})$
$β$	$\arctan(\frac15\cdot\sqrt{5}\cdot\sqrt{3})$	$\arctan((\sqrt{5}-2)\cdot\sqrt{3})$	$\arctan(\frac12\cdot\sqrt{3})$

Diese Informationen wurden zusammengestellt von