1.) Erzeugung von Fließkommazahlen
Da auf der Rätselseite angegeben ist, welche Genauigkeit die zu erzeugende Fließkommazahl haben soll, ist der erste Schritt, die Definition des Gleitkomma-Zahlenformats double IEEE-754 ausfindig zu machen. In Wikipedia findet sich dazu:| Vorzeichen | 1 Bit |
|---|---|
| Mantisse | 52 Bit |
| Exponent | 11 Bit |
Die normalisierte Form einer Gleitkommazahl muss aber bei der Mantisse noch ein zusätzliches höchstwertiges Bit berücksichtigen, welches immer 1 ist und deshalb in den kompakten 64 Bit weggelassen wird. Also steht für die Mantisse der Zahlenbereich von 0 bis 253 - 1 = 9007199254740991 zur Verfügung und das ist ungefähr 0 bis 1016 - 1 = 9999999999999999. Deshalb sind die Zufallszahlen auf der Rätselseite auch mit 16 Nachkommastellen ausgegeben.
Wenn man eine solche Zufallszahl mit einer Münze werfen wollte, so sind 53 Würfe erforderlich, jeder Wurf entspricht einem der 53 Bits. Dabei muss hier natürlich nicht an höchster Stelle eine 1 herauskommen, nur das Fließkomma-Format würde die Bits solange nach links verschieben und gleichzeitig den Exponent herunterzählen, bis vorn eine 1 erscheint, die dann aber im Format weggelassen wird. Um letztendlich zur Zufallszahl im Bereich 0 bis <1 zu gelangen, muss noch durch 253 geteilt werden, was beim Fließkommaformat der Exponent macht.
Bei der Erzeugung einer Zufalls mit einem Würfel ist es nicht so offensichtlich, wie oft gewürfelt werden muss. Wenn man jeden Wurf als Stellenwert einer Zahl im 6er-System auffasst, ist aber nur noch zu bestimmen, bei wie vielen dieser Stellen der Wert von 253 - 1 erreicht ist.
| Würfe | Wert | |
|---|---|---|
| 1 | 61 - 1 = 5 | 22.5849625007212 - 1 |
| 2 | 62 - 1 = 35 | 25.1699250014423 - 1 |
| 3 | 63 - 1 = 215 | 27.7548875021635 - 1 |
| 4 | 64 - 1 = 1295 | 210.339850002885 - 1 |
| 5 | 65 - 1 = 7775 | 212.924812503606 - 1 |
| 6 | 66 - 1 = 46655 | 215.509775004327 - 1 |
| 7 | 67 - 1 = 279935 | 218.094737505048 - 1 |
| 8 | 68 - 1 = 1679615 | 220.679700005769 - 1 |
| 9 | 69 - 1 = 10077695 | 223.26466250649 - 1 |
| 10 | 610 - 1 = 60466175 | 225.849625007212 - 1 |
| 11 | 611 - 1 = 362797055 | 228.434587507933 - 1 |
| 12 | 612 - 1 = 2176782335 | 231.019550008654 - 1 |
| 13 | 613 - 1 = 13060694015 | 233.604512509375 - 1 |
| 14 | 614 - 1 = 78364164095 | 236.189475010096 - 1 |
| 15 | 615 - 1 = 470184984575 | 238.774437510817 - 1 |
| 16 | 616 - 1 = 2821109907455 | 241.359400011538 - 1 |
| 17 | 617 - 1 = 16926659444735 | 243.94436251226 - 1 |
| 18 | 618 - 1 = 101559956668415 | 246.529325012981 - 1 |
| 19 | 619 - 1 = 609359740010495 | 249.114287513702 - 1 |
| 20 | 620 - 1 = 3656158440062975 | 251.699250014423 - 1 |
| 21 | 621 - 1 = 21936950640377855 | 254.284212515144 - 1 |
Bei 20 Würfen reicht es noch nicht ganz, aber mit 21 Würfen ist man der geforderten Genauigkeit sicher.
Mit dem Roulette geht es genauso. hier wird nur statt der 6 eine 37 einzusetzen sein:
| Würfe | Wert | |
|---|---|---|
| 1 | 371 - 1 = 36 | 25.209453365629 - 1 |
| 2 | 372 - 1 = 1368 | 210.418906731258 - 1 |
| 3 | 373 - 1 = 50652 | 215.628360096887 - 1 |
| 4 | 374 - 1 = 1874160 | 220.837813462516 - 1 |
| 5 | 375 - 1 = 69343956 | 226.047266828145 - 1 |
| 6 | 376 - 1 = 2565726408 | 231.256720193774 - 1 |
| 7 | 377 - 1 = 94931877132 | 236.466173559403 - 1 |
| 8 | 378 - 1 = 3512479453920 | 241.675626925032 - 1 |
| 9 | 379 - 1 = 129961739795076 | 246.885080290661 - 1 |
| 10 | 3710 - 1 = 4808584372417848 | 252.094533656289 - 1 |
| 11 | 3711 - 1 = 177917621779460412 | 257.303987021918 - 1 |
Mit 11 Würfen der Kugel beim Roulette ist man auf der sicheren Seite.
Nun kann man ganz allgemein nach der Anzahl der Würfe $n$ fragen, wenn die Möglichkeiten des Generators durch $m$ gegeben ist: $$n=\bigg\lceil\frac{\ln2\cdot53}{\ln m}\bigg\rceil$$ Dabei bedeuten die merkwürdigen Klammern, dass ganzzahlig nach oben gerundet werden soll.
$\ln2\cdot53$ stammt aus dem double IEEE-754 Format.
Die Berechnung der Zufallszahl $x$ kann dann allgemein so erfolgen: $$x=\frac1{m^n}\cdot\sum\limits_{i=1}^{n}(m^{i-1}\cdot w_i)$$ wobei $w_i$ die Ergebnisse der $n$ Würfe bedeutet. Es ist darauf zu achten, dass diese Wurfwerte nur von $0$ bis $m-1$ in diese Formel eingesetzt werden dürfen, also beim Würfeln nicht die gewürfelten Zahlen von 1 bis 6, sondern jeweils um eins vermindert.
2.) mit einem Würfel Wochentage bestimmen
Klar ist: mit einem Wurf geht das nicht. Deshalb versuchen wir es mit zwei Würfen, $w_1$ und $w_2$. Dabei gibt es 36 Möglichkeiten, also viel mehr als nötig. Aber man kann die Zahl $(6\cdot w_1+w_2)$ durch $7$ teilen und nur den Rest für die Bestimmung des Wochentags benutzen, z.B. 0 = Sonntag, 1 = Montag usw. Dabei muss eigentlich auch hier für $w_1$ und $w_2$ der Wertebereich von 0 bis 5 eingesetzt werden (s.o.), aber bei der Division durch $7$ ist das unerheblich, der Rest behält den selben Wert. Nur eins muss beachtet werden: 36 ist kein Vielfaches von 7 und deshalb muss eine Möglichkeit durch eine Zusatzregel gestrichen werden. Das kann die Wurfkombination (1,1), (2,2) ... (5,5) oder (6,6) sein, also solche mit einem Teilungsrest von $0$, aber nur eine davon. Sinnvollerweise nimmt man (6,6) und bestimmt dann: nochmal würfeln. Auf diese Weise wird die durchschnittliche Wurfzahl leicht über $2$ ansteigen, nämlich auf $2\frac1{18}$.3.) Polyeder zum Bestimmen von Wochentagen mit einem Wurf
Der Würfel als Polyeder kommt nicht in Frage, weil er nur 6 Seiten hat.
Es muss also ein Polyeder mit 7 Seiten sein oder ein Vielfaches davon.
Das allein ist aber nur eine notwendige Bedingung, sie ist nicht hinreichend,
weil die Wahrscheinlichkeit für alle Endlageflächen gleich groß sein muss.
Ein Negativbeispiel ist der rechts abgebildete rotierende Johnson-Körper J51 mit Namen "dreifach erweitertes Dreiecksprisma".
Obwohl er ausschließlich von 14 deckungsgleichen gleichseitigen Dreiecken begrenzt ist sieht man sofort,
dass diese Flächen nicht mit gleicher Wahrscheinlichkeit zur Endlage werden,
denn die Winkel an den Kanten sind sehr unterschiedlich und das beeinflusst das Rollverhalten.
Wie kann man also die Gleichberechtigung für die Wahrscheinlichkeit herstellen? Regelmäßige Polygone als Begrenzungsflächen sind nicht gefordert. Allerdings scheint die Gleichheit aller zur Endlage werdenden Flächen eine sinnvolle Forderung zu sein. Darüber hinaus ist eine gewisse Rotationssymmetrie auch wichtig. Hier kommen nun zwei Beispiele für gelungene Polyeder mit den geforderten Eigenschaften:
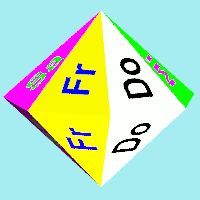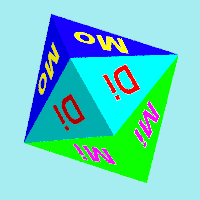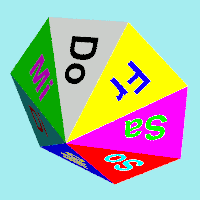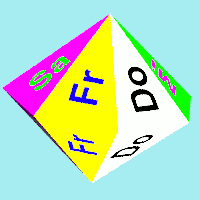
Das rechte Polyeder ist ein 7-seitiges regelmäßiges Prisma mit aufgesetzten 7-seitigen Pyramiden. Die Pyramiden dienen nur dazu, dass dort keine Endlagen ermöglicht werden und nur die 7 Seiten des Prismas als Wurfergebnis bleiben. Dazu ist aber folgende Bedingung einzuhalten: $$h>\frac{2r^2}a \\ \text{mit} \\ a=\text{Höhe des Prismas} \\ h=\text{Höhe der Pyramiden} \\ r=\text{Inkreisradius des 7-Ecks} $$ Diese Bedingung bedeutet, dass das Lot vom Schwerpunkt auf die Ebene einer Dreiecksfläche der Pyramiden außerhalb dieser Fläche auftrifft.
Eine etwas seltsame Variante ist ein regelmäßiges 5-eckiges Prisma. Dabei ist völlig unklar, wie sich die Wahrscheinlichkeiten auf die unterschiedlichen Flächen verteilen. Die erste Form (Bild unten) bevorzugt sicher die Fünfecke. Bei der Untersten ist es genau anders herum. Da sind die Rechtecke im Vorteil. Wenn man nun die Höhe so einstellt, dass ein Gleichstand entsteht (Mitte), ist das auch eine Lösung dieses Rätsels. Eine Berechnung der passenden Höhe widersetzt sich hartnäckig, aber durch Ausprobieren kann man sich der idealen Höhe annähern.
| Wochenende wird bevorzugt |  |
| etwa ausgeglichen |  |
| Wochentage werden bevorzugt |  |
Diese Informationen wurden zusammengestellt von