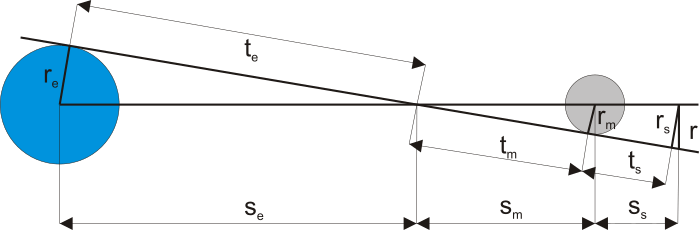
1.) Bezeichnungen und Beschreibungen
$$\begin{align}
G &= \text{Gravitationskonstante} \\
V &= \text{Massenverhältnis Erde zu Mond} \\
r_e &= \text{Radius der Erde} \\
r_m &= \text{Radius des Mondes} \\
m_e &= \text{Masse der Erde} \\
m_m &= \text{Masse des Mondes} \\
m &= \text{Probemasse am Lagrangepunkt} \\
d &= \text{Abstand der Schwerpunkte von Erde und Mond} \\
d_e &= \text{Abstand des Schwerpunkts der Erde vom Lagrangepunkt} \\
d_m &= \text{Abstand des Schwerpunkts des Mondes vom Lagrangepunkt} \\
d_x &= \text{Abstand des Schwerpunkts des Erde-Mond-Systems vom Lagrangepunkt} \\
\omega &= \text{Kreisfrequenz des Erde-Mond-Systems} \\
T &= \text{siderische Umlaufzeit aller Massen um den gemeinsamen Schwerpunkt} \\
f_e &= \text{Anziehungskraft zwischen Erde und Probemasse am Lagrangepunkt} \\
f_m &= \text{Anziehungskraft zwischen Mond und Probemasse am Lagrangepunkt} \\
f_z &= \text{Zentripedalkraft einer Probemasse am Lagrangepunkt} \\
\overrightarrow{e_e} &= \text{Richtung des Einheitsvektors von Erde zum Lagrangepunkt} \\
\overrightarrow{e_m} &= \text{Richtung des Einheitsvektors von Mond zum Lagrangepunkt} \\
\overrightarrow{e_z} &= \text{Richtung des Einheitsvektors vom Schwerpunkt des Erde-Mond-Systems zum Lagrangepunkt} \\
\end{align}$$
$$\begin{align}
x_e &= \text{x-Koordinate des Schwerpunkts der Erde} \\
x_m &= \text{x-Koordinate des Schwerpunkts des Mondes} \\
x &= \text{x-Koordinate des Lagrangepunkts} \\
y &= \text{y-Koordinate des Lagrangepunkts} \\
\end{align}$$
2.) gegebene und leicht zu berechnende Größen
$$
\begin{align}
V &= 81,30059 \\
d &= 3,84400\cdot 10^{8}\; m \\
r_e &=6,37800\cdot 10^{6}\;m \\
r_m &=1,73800\cdot 10^{6}\;m \\
x_e &= -d\cdot\frac{1}{V+1} = -4,67068\cdot 10^{6}\; m \\
x_m &= d\cdot\frac{V}{V+1} = 3,79729\cdot 10^{8}\; m \\
\end{align}
$$
Für dieses Rätsel nicht erforderlich (kürzt sich später raus):
$$\rand
{\begin{align}
G &= 6,67259\cdot 10^{-11}\; m^3kg^{-1}s^{-2} \\
T &= 27,32166 \; d=2,36059\cdot 10^{6}\; s
\end{align}}\tag{Antwort zu Frage 3 des Rätsels}$$
$$\begin{align}
\omega &= \frac{2\pi}{T} = 2,66170\cdot 10^{-6}\; s^{-1} \\
m_e &= \frac{\omega^2\cdot d^3\cdot V}{G\cdot (V+1)}=5,95751\cdot 10^{24}\; kg \tag{1}\\
m_m &= \frac{\omega^2\cdot d^3}{G\cdot (V+1)}=7,32775\cdot 10^{22}\; kg \tag{2}
\end{align}
$$
3.) Berechnung der Koordinaten der Lagrange-Punkte L1 bis L3
$$
f_e \cdot \overrightarrow{e_e} + f_m \cdot \overrightarrow{e_m} = f_z \cdot \overrightarrow{e_z} \\
\frac{G\cdot m_e \cdot m}{ {d_e}^2} \cdot \overrightarrow{e_e} + \frac{G\cdot m_m \cdot m}{ {d_m}^2} \cdot \overrightarrow{e_m} = m \cdot \omega^2 \cdot d_x \cdot \overrightarrow{e_z}\\
\frac{m_e}{ {d_e}^2} \cdot \overrightarrow{e_e} + \frac{m_m}{ {d_m}^2} \cdot \overrightarrow{e_m} =\frac{ \omega^2\cdot d_x}{G} \cdot \overrightarrow{e_z} \\
\frac{m_e}{ {d_e}^3} \cdot \left(\matrix{x-x_e\\y}\right) + \frac{m_m}{ {d_m}^3} \cdot \left(\matrix{x-x_m\\y}\right) =\frac{ \omega^2}{G} \cdot \left(\matrix{x\\y}\right) \\
$$
Wenn man die Komponenten der Vektoren in zwei einzelne Gleichungen schreibt, hat man ein Gleichungssystem ohne Vektoren:
$$
\frac{m_e}{ {d_e}^3} \cdot (x-x_e) + \frac{m_m}{ {d_m}^3} \cdot (x-x_m) -\frac{ \omega^2}{G} \cdot x =0 \tag{3}
$$
$$
y\cdot\left(\frac{m_e}{ {d_e}^3} + \frac{m_m}{ {d_m}^3} -\frac{ \omega^2}{G} \right)=0 \tag{4}
$$
Eine Lösung für die Gleichung (4) ist $y=0$.
Dann wird aus der Gleichung (3) eine Funktion von x, deren Nullstellen zu suchen sind.
$$
f(x)=\frac{m_e}{(x-x_e)|x-x_e|} + \frac{m_m}{(x-x_m)|x-x_m|} -\frac{ \omega^2}{G} \cdot x \\
$$
$m_e$ und $m_m$ wird ersetzt durch die Formel (1) und (2). Dann kürzt sich $\frac{\omega^2}{G}$.
Wenn man $\frac{x}{d}$ durch $u$ substituiert erhält man nach einigen Umformungen eine Funktion von $u$, in der zusätzlich nur noch das Massenverhältnis $V$ auftaucht:
$$
f(u)=\frac{V}{\left(u+\frac{1}{V+1}\right)\left|u+\frac{1}{V+1}\right|} + \frac{1}{\left(u-\frac{V}{V+1}\right)\left|u-\frac{V}{V+1}\right|} - (V+1) \cdot u
$$
Der Kurvenverlauf dieser Funktion zeigt bereits Näherungswerte für die drei Nullstellen:
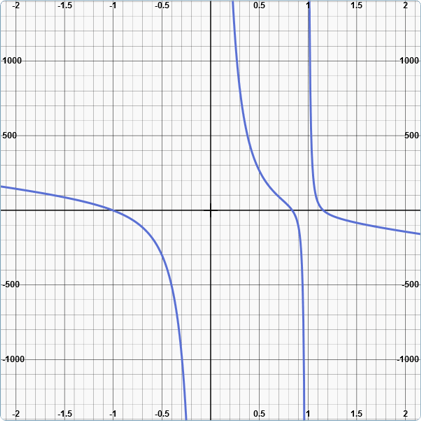
Zur Lösung dieser Gleichung kann das Newton-Verfahren zur schrittweisen Näherung benutzt werden:
$$
u_{n+1} = u_n - \frac{f(u_n)}{f'(u_n)}
$$
Dazu ist noch die 1. Ableitung zu bilden:
$$
f'(u)=-\frac{2}{\left(u-\frac{V}{V+1}\right)^2\left|u-\frac{V}{V+1}\right|}-\frac{2V}{\left(u+\frac{1}{V+1}\right)^2\left|u+\frac{1}{V+1}\right|}-V-1
$$
| $n$ | u1 |
|---|
| 0 | 0,8200000000 |
| 1 | 0,8383195691 |
| 2 | 0,8369265442 |
| 3 | 0,8369151483 |
| 4 | 0,8369151476 |
| f'(u1) | -929,6006986574 |
|---|
| $n$ | u2 |
|---|
| 0 | 1,1500000000 |
| 1 | 1,1554712662 |
| 2 | 1,1556818618 |
| 3 | 1,1556821484 |
| 4 | 1,1556821484 |
| f'(u2) | -607,4483590201 |
|---|
| $n$ | u3 |
|---|
| 0 | -1,0000000000 |
| 1 | -1,0050366721 |
| 2 | -1,0050626433 |
| 3 | -1,0050626440 |
| 4 | -1,0050626440 |
| f'(u3) | -248,6615663985 |
|---|
Damit sind die Koordinaten in der Schreibweise von Ortsvektoren der Lagrange-Punkte 1 bis 3 anzugeben:
$$
\rand{
\begin{align}
L_1&=\left(\matrix{x_1\\y_1}\right)=\left(\matrix{u_1\cdot d\\0}\right)=\left(\matrix{3,21710\cdot 10^{8}\;m\\0}\right) \\
L_2&=\left(\matrix{x_2\\y_2}\right)=\left(\matrix{u_2\cdot d\\0}\right)=\left(\matrix{4,44244\cdot 10^{8}\;m\\0}\right) \\
L_3&=\left(\matrix{x_3\\y_3}\right)=\left(\matrix{u_3\cdot d\\0}\right)=\left(\matrix{-3,86346\cdot 10^{8}\;m\\0}\right)
\end{align}
}\tag{Teilantwort zu Frage 1 des Rätsels}
$$