Lösungsbeschreibung des Preisrätsels vom Juli 2013

Als Pluto mal der 8. Planet war

Das wesentliche Ziel dieses Rätsels ist es die Datenbank der NASA kennen und nutzen zu lernen. Wer allerdings mit vergleichbar genauen anderen Programmen arbeiten will, kann anschließend die Ergebnisse hiermit vergleichen und dann vielleicht eine neue Beurteilung über die Genauigkeit anstellen.

Mit zunehmender Messgenauigkeit sind aber auch neue Betrachtungen über die Bezugssysteme für Raum und Zeit erforderlich. Mit dem räumlichen Koordinatensystem haben wir in unserem Rätsel das geringste Problem. Da nur nach Distanzen gefragt wurde, ist das Ergebnis für alle Koordinatensysteme gleich. Wichtig ist nur, den richtigen Anfangs- und Endpunkt zu definieren.
Bei der Zeit ist aber streng darauf zu achten, dass man die Angaben zur Zeit richtig macht, denn da unterscheiden sich die Ergebniswerte bei der geforderten Genauigkeit schon etwas. Das in der Astronomie übliche Zeitsystem ab 1952 war die Ephemeridenzeit (ET), im Unterschied zur Weltzeit (UT). Es war schon länger aufgefallen, dass die Weltzeit ein ungleichförmiges Zeitmaß war. Zum Beispiel war bei der Rückrechnung der Sonnenfinsternisse früherer Zeiten die Rotationsstellung der Erde nicht so wie erwartet. Die Berichte über Sonnenfinsternisbeobachtungen gaben aber genau Auskunft über den Standort des Beobachters und daher auch über die tatsächliche Rotationsstellung der Erde. Es war daraus abzuleiten, dass die Rotation der Erde zwar langsam aber über tausende von Jahren aufsummiert deutlich abnimmt. Die Nachfolge der ET wurde ab 1984 die Terrestrische Dynamische Zeit (TDT). Sie ist das beste gleichmäßig ablaufende Zeitmaß für die Erdoberfläche. Der Nachfolger der UT wurde die Koordinierte Weltzeit (UTC). Damit sind die Sekunden zwar wieder gleich lang wie die Sekunden der TT, aber wegen der ungleichförmigen Erdrotation und deren Verlangsamung müssen hin und wieder Schaltsekunden eingefügt werden. Die Erkenntnisse der Relativitätstheorie führen noch zu einer weiteren Zeit, die unabhängig von der Rotation der Erde und ihrer Bahn um die Sonne ist, denn durch die beschleunigten Bewegungen auf der Erdoberfläche gehen Uhren etwas langsamer als im ruhenden Zustand. Hier sind wir jetzt beim Zeitsystem der NASA mit der Baryzentrischen Dynamischen Zeit (TDB) oder einfach Coordinate Time (CT). Dies ist eine aus der TDT abgeleitet berechnete Zeit, die z.B. eine Atomuhr zeigt, die im Schwerpunkt des Sonnensystems ruht. Es gab aber bei der Definition noch einige Unklarheiten und so musste 1991 nochmals eine Korrektur angebracht werden, die zum heutigen Standard führte: aus TDT wurde der identische Nachfolger TT und die Eigenzeiten Koordinatenzeit (TCG) und Baryzentrische Koordinatenzeit (TCB) wurden eingeführt. Der Unterschied zur TDT ist bei beiden sehr gering.

Zeitdefinitionen
seit gleichmäßig ablaufend von der Erddrehung abgeleitet
1884 mittlere Greenwich-Zeit
GMT (Greenwich Mean Time)
1928 Weltzeit
UT (Universal Time)
1952 Ephemeridenzeit
ET (Ephemeris Time)
1968 Internationale Atomzeit
TAI (Temps Atomique International)
gewichteter Mittelwert vieler Atomuhren 		Weltzeit
UT1 (wie UT aber korrigiert
um Einflüsse der Polschwankungen)
1972 Koordinierte Weltzeit
UTC ( engl.: Coordinated Universal Time
franz.: Temps universel coordonné)
UTC = TAI ± Schaltsekunden, sodass UTC und
UT1 nie weiter als 0,7s voneinander abweichen
1984 Dynamische Zeit
TD (temps dynamique)

Terrestrische Dynamische Zeit
TDT (temps dynamique terrestrique)
Bezug: Erdmittelpunkt
TDT = TAI + 32,184s
(Anpassung an ET am 1. Jan. 1977 0 Uhr TAI)

Baryzentrische Dynamische Zeit
TDB (temps dynamique barycentrique)
oder CT (Coordinate Time)
Bezugspunkt: Mittelpunkt des Sonnensystems
TDT - TDB < 5ms
1991 Terrestrische Zeit
TT (temps terrestrique)
identischer Nachfolger von TDT

Geozentrische Koordinatenzeit
TCG (temps coordonné géocentrique)
wie TDT aber ohne Gravitation der Erde
pro Jahr 22ms schneller als TT

Baryzentrische Koordinatenzeit
TCB (temps coordonné barycentrique)
wie TDB aber ohne Gravitation des Sonnensystems


zur 1.) und 2.) Frage

Für die Beantwortung sind die Entfernungen der beiden (damals noch) Planeten Neptun und Pluto für eine Reihe von Zeitpunkten zu ermitteln. Im Rätsel wurde schon auf die Internetseite der NASA hingewiesen und auf die Möglichkeit des freien Zugangs zu allen Daten. Ich habe den Telnet-Zugang ausprobiert, der sich dann vorzüglich eignet, wenn man die Kommandos programmgesteuert senden und die Antworten ebenso auswerten kann. Email fand ich zu umständlich. Für die hier gewünschten Daten bietet sich der HTML-Zugang über den Browser an. Dazu ist die Bedienungsoberfläche auf der Seite https://ssd.jpl.nasa.gov/horizons/. Da das Datum 7. Feb. 1979 für den Beginn der Ära Plutos als 8. Planet aus der Wikipediaseite bekannt ist, kann man für einen ersten Überblick folgende Eingaben machen:



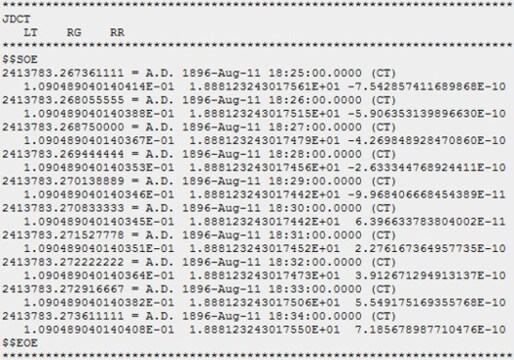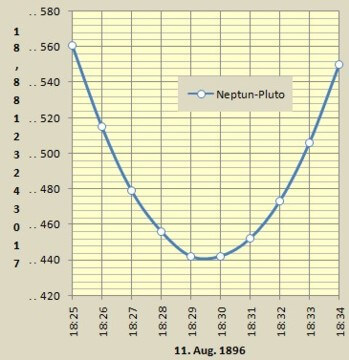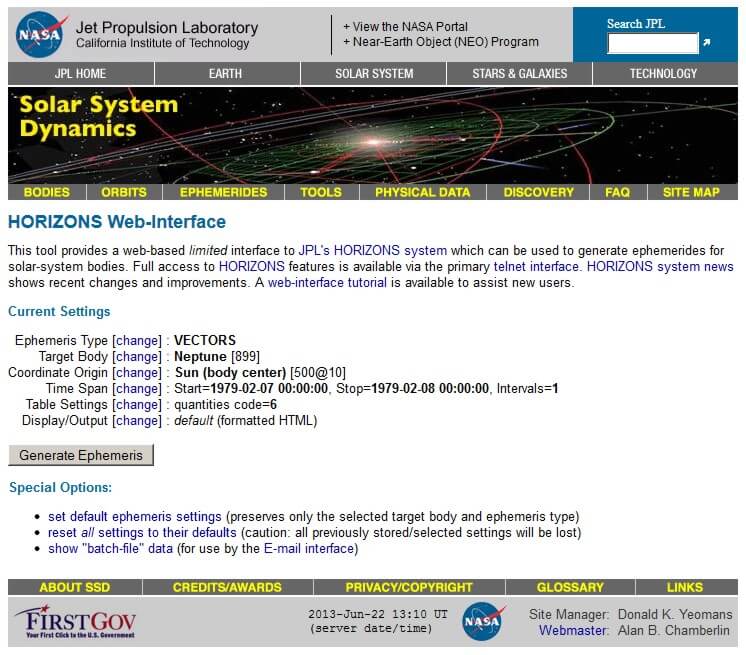
Das für uns interessante Ergebnis ist dies:



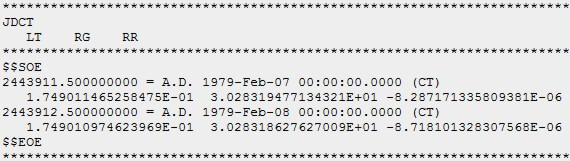
Die Abkürzungen haben folgende Bedeutung:

JDCTJulianisches Datum in "Coordinate Time"
LTLichtlaufzeit für die Strecke unter RG in Tagen
RGAbstand der Körpermittelpunkte in Astronomischen Einheiten
RRRadialgeschwindigkeit (Komponente in Richtung von RG) in AE/Tag


Davon benutzen wir dann nur RG und die zugehörigen Zeitpunkte.
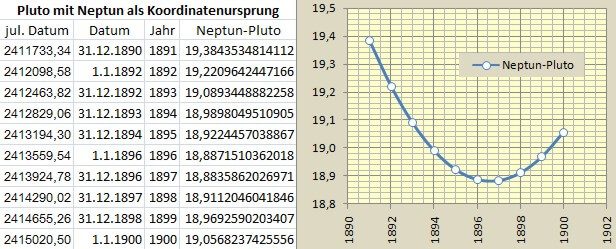
Wenn man das Gleiche nun für Pluto macht, kann man z.B. mit EXCEL ein Diagramm erstellen.
Um die Lage des Kreuzungspunktes wie mit der Lupe genauer lokalisieren zu können
sind die beiden Achsen wie folgt stark gespreizt dargestellt:



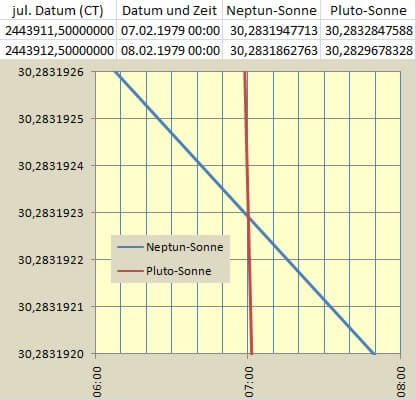
Damit hat man bereits eine sehr gute Annäherung:

Zeitpunkt etwa 7. Feb. 1979 7:00 Uhr
Entfernung etwa 30,2831923 AE

Aber man darf nicht vergessen, dass es sich um eine lineare Interpolation handelt. Die erhaltenen Werte sind Ausgangspunkt für eine erneute Anfrage bei der NASA, bei der der Zeitbereich drastisch eingeengt wird. Zusätzlich benötigen wir noch den Abstand von Neptun und Pluto. Das kann auf zweierlei Weise bestimmt werden:
a) man fragt die NASA-Datenbank zusätzlich nach den ($x$,$y$,$z$)-Koordinaten für beide Körper ab
(Table Settings: quantities code = 1 oder 2) und berechnet deren Abstand $d$ mit: $$ \sand{d=\sqrt{\left(x_{Neptun}-x_{Pluto}\right)^2+\left(y_{Neptun}-y_{Pluto}\right)^2+\left(z_{Neptun}-z_{Pluto}\right)^2}} $$ oder b) man fragt nach dem Abstand direkt, indem z.B. Neptun als Koordinatenursprung anstelle der Sonne eingetragen wird.
In jedem Fall kommt man zum gleichen Ergebnis und kann dann alles in des endgültige EXCEL-Diagramm zusammenfassen.
Dabei ist die zweite vertikale Achse für den Abstand (rechts) so einzustellen,
dass die Abstandsfunktion auf dem Schnittpunkt der beiden anderen Linien zu liegen kommt.
Das Ergebnis sieht dann so aus:



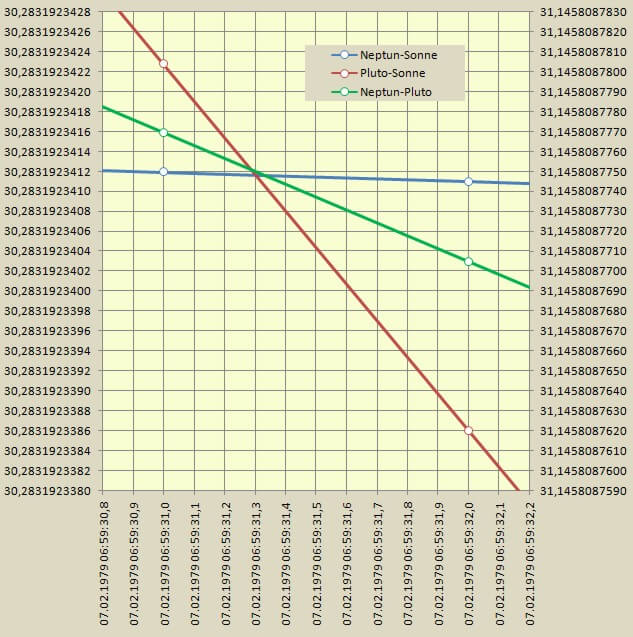
Das oben beschriebene Verfahren lässt sich nun genauso auf den zweiten Zeitpunkt (11. Feb. 1999) anwenden und daraus geht das folgende Diagramm hervor:



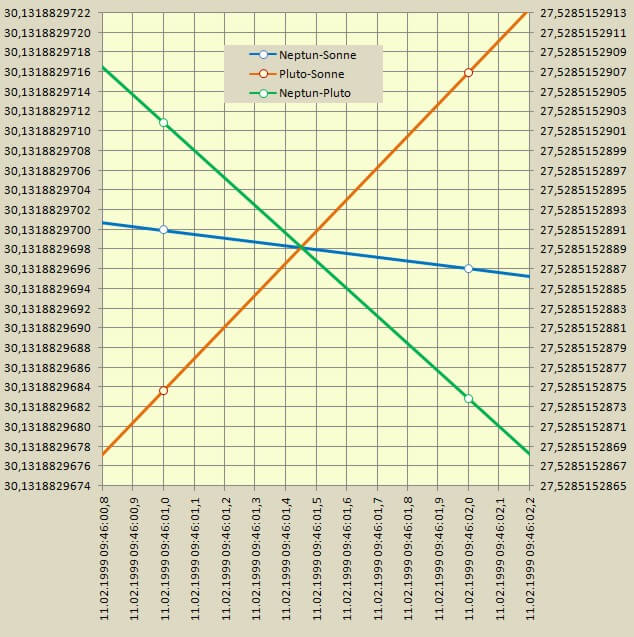
Die Schnittpunkte der beiden Diagramme liefern nun alle Daten zur Beantwortung der Fragen 1.) und 2.):

ZeitpunktEntfernung zur SonneEntfernung Neptun-Pluto
7. Februar 1979 6:59:31,3 CT30,2831923412 AE31,1458087750 AE
11. Februar 1999 9:46:01,45 CT30,1318829698 AE27,5285152889 AE



zur 3.) Frage

Bei der Frage nach dem minimalen Abstand wird sich auch nicht annähernd eine lineare Funktion ergeben. Es ist eher so wie auf der Autobahn. Zwei Fahrzeuge sind mit unterschiedlicher Geschwindigkeit unterwegs, das langsamere auf der rechten Spur. Das schnellere Fahrzeug nähert sich zum Überholvorgang auf der linken Spur. Der Abstand der Köpfe der beiden Fahrer wird sich noch bei größerem Abstand nahezu linear verkleinern. Dann beginnt der Überholvorgang und der Abstand wird relativ langsam auf einen minimalen Wert absinken. Wenn nach dem Überholvorgang der Abstand wieder groß geworden ist, wird er sich wieder nahezu linear vergrößern. Zusammengefasst hat der Verlauf der Abstandsfunktion große Ähnlichkeit mit einer Parabel. Genauso ist es mit Planeten auf ihren "Autobahnspuren". Die Abfrage der NASA-Datenbank sollte zunächst eine größere Anzahl von Abstandsdaten liefern über einen Zeitbereich, der vor 1900 liegt, also z.B. von 1875 bis 1900 für jeden Jahresanfang. Hier sind die nötigen Einstellungen:


Wenn man sich die Zahlenwerte für RG (Abstand) ansieht, fällt auf, das ein Minimum etwa bei 1896/1897 liegt. Um die erwartete parabelförmige Kurve darzustellen, nimmt man nur die letzten 10 von den 25 Werten und erzeugt mit EXCEL wieder ein Diagramm:



Nun ist der Weg klar. Durch zwei oder drei weitere Stufen mit Einengung des Zeitbereichs kommt man zum finalen Diagramm, aus dem man leicht den Zeitpunkt und den Abstand ablesen kann. Eine Schwierigkeit kommt von EXCEL selbst: in meiner Version (2007) sind Datumsberechnungen vor 1900 nicht ohne eigenständige Makros möglich und das Diagramm erlaubt auch keine Werte vor 1900. Man kann dieses Problem umgehen, indem man sich nur auf das Julianische Datum bezieht oder aber eine Abtrennung der hinteren Stellen bzw. beim Datum nur die Uhrzeit verwendet. Die Beschriftung der Achse liefert den "vorderen" Teil. Hier folgt nun meine feinste zeitliche Auflösung im Kommando an die NASA-Datenbank und das dazu gehörige Diagramm.






Die Antwort auf die 3.) Frage ist also:

Am 11. August 1896 gegen 18:29:30 CT war Pluto das letzte mal dem Neptun am nächsten mit einem Abstand von 18,8812324301744 AE.

Abschließende Bemerkungen:

Natürlich sind die hier angegebenen Ergebnisse von ihrer Genauigkeit etwas fragwürdig aber letztlich sicher die genauesten Daten, die zurzeit verfügbar sind. Immerhin kennen wir dank NASA die Entfernung des Mondes für jeden Zeitpunkt seit den 70er Jahren auf wenige Millimeter genau. Wer eine Sonde zum Pluto schickt ist auch darauf angewiesen diesen nach einer Flugzeit von rund 10 Jahren präzise zum Rendezvous zu treffen. Wer sich für die Flugroute und die bereits durchgeführten Kurskorrekturen von New Horizons informieren will, sollte die Wikipediaseite lesen. Ab Mitte 2015 werden die Bahndaten von Pluto dank New Horizons noch einen Tick besser sein.

Diese Informationen wurden zusammengestellt von

Kurzbewertung dieser Information:
sehr gut gut befriedigend
ausreichend mangelhaft ungenügend