1.) Bezeichnungen für Knoten und Kanten
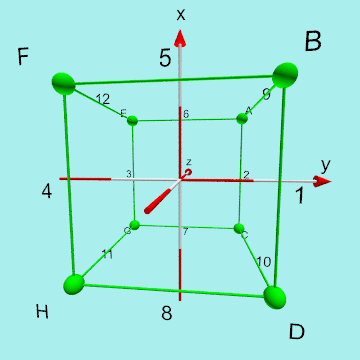
Bild 1
Dabei sind die Eckpunkte des Würfels (Knoten des Netzwerks) mit den großen Buchstaben von A bis H benannte und die Kanten des Würfels (auch Kanten des Netzwerks) mit den Zahlen von 1 bis 12 beschriftet. Diese Festlegung ist absolut willkürlich und würde bei veränderter Festlegung keinen Einfluss auf die Ergebnisse für dieses Rätsel haben.
Das Koordinatensystem ist ebenfalls willkürlich und dient dazu, die Rotationen um verschiedene Achsen festzulegen.
Auch für Personen, die eine gute räumliche Vorstellung von rotierten Körpern haben, ist es fast unmöglich, dieses Rätsel ohne Rechnerunterstützung zu lösen. Deshalb wird hier auch sehr ausführlich der Weg der Programmierung beschrieben. Dazu wird der Code in der Programmiersprache PHP gezeigt, der auch in dieser Internetseite beim Aufruf serverseitig abläuft und alle Ergebnisse jeweils neu berechnet. Andere Programmiersprachen sind aber genauso geeignet.
2.) Anzahl aller Varianten
Die erste Frage kann noch mit einfacher Mathematik beantwortet werden. Es gib 12 Würfelkanten, denen 7 Netzwerkkanten in allen Variationen zugeordnet werden sollen. Dabei ist die Reihenfolge nicht von Bedeutung, denn es würde beim Austausch zweier Kanten trotzdem das gleiche Netzwerk entstehen. Zur Berechnung wird eine Formel aus der Kombinatorik verwendet: $$\rand{ \text{Anzahl aller Varianten}={n\choose k}={12\choose 7}= 792}$$3.) allgemeiner Programmaufbau
Da nun klar ist, das mit einer recht großen Anzahl von Varianten begonnen werden muss, ist eine Vorgehensweise für das Aussortieren der Wiederholungen zu planen, die durch Drehungen des Würfels um alle seine Achsen sich ergeben und in der Zahl 792 enthalten sind. Es ist sinnvoll, eine erste Liste von der Länge 792 mit Zahlen zu füllen, die den jeweils einzigartigen Typ einer Variation kennzeichnet. Gleichzeitig wird eine zweite Liste aufgebaut, die die Eigenschaften dieser als verschieden von bisher gefundenen Varianten sammelt. Dabei entsteht automatisch die Antwort auf die zweite Frage, nämlich die Länge dieser zweiten Liste. Abschließend kann dann aus den abgespeicherten Eigenschaften die Antwort zur dritten Frage abgeleitet werden.4.) das Durchlaufen der ersten Liste
Es macht keinen Sinn, die erste Liste mit den Zahlen von 1 bis 792 zu durchlaufen, denn diese Zahlen stehen in keiner erkennbaren Verbindung zu der Art des Netzwerks. An einem sehr kleinen Beispiel soll gezeigt werden, wie die Vorgehensweise stattdessen geplant ist.Die folgende Tabelle zeigt die Variationen, wenn $n=5$ und $k=3$ ist. Das ergibt ${5\choose 3}=10$ Varianten. Der Schlüssel ist der assoziative Index für die Liste und entsteht aus den Kanten des Netzwerks.
| lfd. Nr | Variation | Schlüssel |
|---|---|---|
| 1 | 1,2,3 | 123 |
| 2 | 1,2,4 | 124 |
| 3 | 1,2,5 | 125 |
| 4 | 1,3,4 | 134 |
| 5 | 1,3,5 | 135 |
| 6 | 1,4,5 | 145 |
| 7 | 2,3,4 | 234 |
| 8 | 2,3,5 | 235 |
| 9 | 2,4,5 | 245 |
| 10 | 3,4,5 | 345 |
Tabelle 1
Man sieht hier, wie sich die Variationen entwickeln. Die erste der drei Ziffern durchläuft die Werte von 1 bis 3, die zweite die Werte von 2 bis 4, die dritte von 3 bis 5, und das so, dass die jeweilige Ziffer immer größer als ihr linker Nachbar ist, also eine aufsteigend sortierte Reihenfolge der drei Ziffern. Das kann man mit dem folgenden Programmteil auch für $n=12$ und $k=7$ erreichen:
for ($a1=1;$a1<=6;$a1++)
{
for ($a2=$a1+1;$a2<=7;$a2++)
{
for ($a3=$a2+1;$a3<=8;$a3++)
{
for ($a4=$a3+1;$a4<=9;$a4++)
{
for ($a5=$a4+1;$a5<=10;$a5++)
{
for ($a6=$a5+1;$a6<=11;$a6++)
{
for ($a7=$a6+1;$a7<=12;$a7++)
{
$a=[$a1,$a2,$a3,$a4,$a5,$a6,$a7];
typ($a);
}
}
}
}
}
}
}Programmcode 1
Man könnte auch zum gleichen Ergebnis gelangen, wenn man statt der sieben geschachtelten Schleifen eine einzige in einem Unterprogramm mit Abbruchkriterium einsetzen würde und dieses Unterprogramm sich selbst aufrufen lässt. Diese iterative Methode ist zwar eleganter und flexibler aber bei weitem nicht so übersichtlich.5.) verschiedene Unterprogramme
In der Zeile 16 von Programmcode 1 befindet sich der Aufruf eines Unterprogramms, welches nacheinander mit den 792 Werten der Varianten versorgt wird. Darin wird dann auch der Schlüssel (wie in Tabelle 1) für den Zugriff auf die Elemente der ersten Liste (assoziatives Array: $liste[ ]) erzeugt.Falls an dieser Stelle in der ersten Liste noch kein Eintrag existiert, wird die laufende Nummer für neue Varianten (Variable: $nummer) dort eingetragen (Programmcode 2 Zeile 16). Das geschieht aber nicht nur für eine Variante, sondern auch für alle $4\cdot 6=24$ (4 Himmelsrichtungen, 6 Grundseiten) durch Drehungen entstehende Varianten gleichen Typs, die im Unterprogramm in Zeile 12 von Programmcode 2 erzeugt werden.
In der zweiten Liste (Array: $typen[ ]) wird ein Eintrag dieses neuen Typs mit dem Schlüssel der laufenden Nummer und der Zusatzdimension "Kanten" vorgenommen. Ein weiterer Eintrag startet die Zählung dieses Typs mit dem Wert 1 in der Zusatzdimension "Zahlen". Anschließend wird die Nummer um eins erhöht.
Falls schon ein Eintrag in der ersten Liste vorliegt wird der Eintrag als Schlüssel für die zweite Liste benutzt, um dort die "Zahlen"-Dimension um eins zu erhöhen.
Dieser Weg scheint umständlich, aber ist sehr effektiv bei der Findung der tatsächlichen Zahlen für jeden Typ. Die 24 Einträge erzeugen nämlich nicht immer 24 neue Varianten eines Typs. Es werden teilweise schon erfolgte Einträge mit dem gleichen Wert überschrieben. Darum muss sich die gewählte Methode aber nicht kümmern, da sie von den Überschreibungen nichts sieht. Sie kommt erst später an die Speicherzellen und erhöht dann den Zählerstand nur einmal (Programmcode 2 Zeile 10).
function typ($a)
{
global $liste;
global $typen;
global $nummer;
$key = $a[0].$a[1].$a[2].$a[3].$a[4].$a[5].$a[6];
if(array_key_exists ($key, $liste))
{
$typen[$liste[$key]]["zahlen"]++;
}else{
$g = gleiche($a);
for($i=0; $i<24; $i++)
{
$key = $g[$i][0].$g[$i][1].$g[$i][2].$g[$i][3].$g[$i][4].$g[$i][5].$g[$i][6];
$liste[$key] = $nummer;
}
$typen[$nummer]["kanten"] = $a;
$typen[$nummer]["zahlen"] = 1;
$nummer++;
}
}Programmcode 2
Wie im einzelnen die 24 gleichen, aber durch Drehungen unterschiedlich erscheinenden Varianten gefunden werden, wird im folgenden Unterprogramm gezeigt:
function gleiche($sample)
{
sort($sample);
$g[0] = $sample;
$g[1] = rotx($g[0]);
$g[2] = rotx($g[1]);
$g[3] = rotx($g[2]);
$g[4] = roty($g[0]);
$g[5] = rotx($g[4]);
$g[6] = rotx($g[5]);
$g[7] = rotx($g[6]);
$g[8] = roty($g[4]);
$g[9] = rotx($g[8]);
$g[10] = rotx($g[9]);
$g[11] = rotx($g[10]);
$g[12] = roty($g[8]);
$g[13] = rotx($g[12]);
$g[14] = rotx($g[13]);
$g[15] = rotx($g[14]);
$g[16] = rotz($g[0]);
$g[17] = rotx($g[16]);
$g[18] = rotx($g[17]);
$g[19] = rotx($g[18]);
$g[20] = rotz(rotz($g[16]));
$g[21] = rotx($g[20]);
$g[22] = rotx($g[21]);
$g[23] = rotx($g[22]);
return $g;
}Programmcode 3
Dabei sind die Unterprogramme $\text{rotx()}$, $\text{roty()}$ und $\text{rotz()}$ Rotations-Tranformationen um die jeweilige x-, y- oder z-Achse. Die Tranformation $\text{\$trans} = [2,3,4,1,9,12,11,10,6,7,8,5]$ für eine 90°-Drehung um die x-Achse bedeutet ein Austausch der Kanten:| von | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| nach | 2 | 3 | 4 | 1 | 9 | 12 | 11 | 10 | 6 | 7 | 8 | 5 |
was am Bild 1 nachzuvollziehen ist. Nach jeder Drehung müssen die Kanten in aufsteigender Reihenfolge sortiert werden, denn nur so findet man in der ersten Liste entsprechende Einträge.
function rotx($sample) // rotiert 90° um x-Achse
{
$trans = [2,3,4,1,9,12,11,10,6,7,8,5];
for ($i=0; $i<count($sample); $i++)
{
$result[$i] = $trans[$sample[$i]-1];
}
sort($result);
return $result;
}
function roty($sample) // rotiert 90° um y-Achse
{
$trans = [9,10,11,12,6,7,8,5,2,1,4,3];
for ($i=0; $i<count($sample); $i++)
{
$result[$i] = $trans[$sample[$i]-1];
}
sort($result);
return $result;
}
function rotz($sample) // rotiert 90° um z-Achse
{
$trans = [8,7,6,5,1,2,3,4,10,11,12,9];
for ($i=0; $i<count($sample); $i++)
{
$result[$i] = $trans[$sample[$i]-1];
}
sort($result);
return $result;
}Programmcode 4
6.) Datenausgabe
Eigentlich ist schon fast alles fertig und versteckt sich nur in der zweiten Liste. Die Antwort auf die zweite Frage ist die Länge der zweiten Liste, was gleichbedeutend mit dem Wert von $nummer ist. $$\rand{ \text{Anzahl verschiedener Typen}=38 }$$Eine vollständige Tabelle aller Typen und deren Eigenschaften ist für dieses Rätsel nicht verlangt, aber hier sinnvoll, um die Vorgehensweise zu erkennen.
Die Ausgabe dieser Daten bedeutet, dass man alle Typen der zweiten Liste durchläuft und die Inhalte zeilenweise ausgibt.
Währenddessen werden noch einige wichtige Aktionen durchgeführt, die die Eigenschaften des jeweiligen Netzwerks erforschen.
Es ist z.B. von Interesse, wie viele Kanten an einem Knoten zusammenkommen. Die Zahl ist im Bereich von 0 bis 3. Bei einem Knoten mit 0 Kanten ist klar, das er nicht vom Netzwerk erreicht wird, also es ein unvollständiges Netzwerk ist. Bei einem Knoten mit 3 Kanten ist es keinesfalls ein lineares, sondern ein verzweigtes Netzwerk. Ein unzusammenhängendes Netzwerk, welches zwar an jedem Knoten mindestens eine Kante hat, zerfällt aber in zwei Teile. Dies ist immer dann der Fall, wenn sich in einem Teil des Netzwerks ein Ring bildet. Der Ring bindet eine Kante mehr als erforderlich ein, die an anderer Stelle zur Anbindung fehlt.
Die obigen Eigenschaften sind also noch aus den bekannten Kanten auszufiltern.
Im Programm wird jeder Kante nach folgendem Prinzip eine Zahl zugeordnet:
// H G F E D C B A
$punkte = [ bindec('0000000001000100'), // 1
bindec('0000000000010001'), // 2
bindec('0001000100000000'), // 3
bindec('0100010000000000'), // 4
bindec('0000010000000100'), // 5
bindec('0000000100000001'), // 6
bindec('0001000000010000'), // 7
bindec('0100000001000000'), // 8
bindec('0000000000000101'), // 9
bindec('0000000001010000'), // 10
bindec('0101000000000000'), // 11
bindec('0000010100000000'), // 12
];Programmcode 5
Die Werte der Kanten sind zeilenweise gelistet, mit der Nummer der Kante als Kommentar rechts außen. Es handelt sich um eine Umwandlung eines Binär-Textes in eine Dezimalzahl. In der Kommentarzeile oben erkennt man die Buchstaben der Knoten. Für jeden Knoten sind 2 Bit reserviert, denn es werden, wie schon oben erwähnt, Zahlen von 0 bis 3 erwartet. Man kann anhand der Abbildung 1 das obige Muster mit den Beziehungen von Knoten und Kanten vergleichen. Z.B. sagt die erste Zeile aus, dass es sich um die Kante 1 handelt, mit den Endpunkten B und D, die jeweils durch eine 1 im Bitmuster gekennzeichnet sind.
Wenn man nun von jeder Kante eines Typs die obige Zahl ausliest und alle sieben addiert, erhält man ein Ergebnis, bei dem in jeweils 2 Bit die Zahl der Kanten am jeweiligen Knoten anliegen. Es muss keine Zuordnung zu bestimmten Knoten geben. Deshalb sind auch keine Rotationen zur Überprüfung erforderlich. Es kann beim durchsehen der Bits gleich ein passendes Ergebnis-Bit für eine Null und ein anderes für eine drei gesetzt werden. Hier folgt der Programmcode:
$kenn = 0;
for($j=0; $j<7; $j++)
{
$kenn += $punkte[$typen[$i]["kanten"][$j]-1];
}
$bit = 0;
for($j=0; $j<=7; $j++)
{
$k = $kenn % 4;
$kenn = ($kenn - $k)/4;
if($k==3) {$bit = $bit | 1;}
if($k==0) {$bit = $bit | 2;}
}Programmcode 6
Damit ist die Information "unvollständig" und "verzweigt" für diesen Typ mit der laufenden Nummer $i bekannt und in der Variablen $bit zur späteren Auswertung abgelegt.Die Erkennung von Ringen ist etwas schwieriger. Zunächst muss man erkennen, dass es nicht nur eine Sorte von Ringen gibt. Die einfachste Form ist der 4er-Ring, der eine Seite des Würfels umrahmt. Dieser kann natürlich auf jeder Würfelseite auftreten und muss erkannt werden. Eine zweite Form ist ein 6er-Ring, der zwei benachbarte Seiten des Würfels umrahmt. Auch hier gilt, das alle gedrehten Ringe dieser Art erkannt werden müssen. Zuletzt gibt es eine Variante des 6er-Rings. Er verbindet auf zwei Wegen mit jeweils drei Kanten zwei gegenüberliegende Knoten des Würfels.
Ein beliebiger Repräsentant jeder Form ist leicht zu finden. Die übrigen werden mit der bereits bekannten Methode von Unterprogramm $gleiche (Programmcode 3) erzeugt. Dann muss nur noch festgestellt werden, ob eines der vielen Ringmuster im jeweiligen Typ der zweiten Liste enthalten ist und wenn ja, dann muss ein weiteres Ergebnis-Bit dafür gesetzt werden. Hier folgt die Fortsetzung von Programmcode 6:
$a = $typen[$i]["kanten"];
$b = [2,3,6,7]; // 4er-Ring
$g = gleiche($b);
if (test($a,$g)) {$bit = $bit | 4;}
$b = [1,3,5,8,11,12]; // 6er-Ring
$g = gleiche($b);
if (test($a,$g)) {$bit = $bit | 4;}
$b = [1,3,5,7,10,12]; // zweiter 6er-Ring
$g = gleiche($b);
if (test($a,$g)) {$bit = $bit | 4;}
if( $bit == 0 ) { $kat[0]++; } // linear
if( (($bit & 1) > 0) && (($bit & 4) == 0)) { $kat[1]++; } // verzweigt
if( ($bit & 2) > 0 ) { $kat[2]++; } // unvollständig
if( (($bit & 2) == 0) && (($bit & 4) > 0)) { $kat[3]++; } // geteilt
$text="";
if( $bit == 0 ) {$text .= "linear ";}
if( ($bit & 1)) {$text .= "verzweigt ";}
if( ($bit & 2)) {$text .= "unvollständig ";}
if( ($bit & 4)) {$text .= "Ring";}Programmcode 7
Wie im Programmcode 7 zu sehen ist, wird auch gleich eine Auswertung der drei Bits durchgeführt. In der Variablen $kat werden die zur jeweiligen Kategorie gehörigen Typen gezählt und damit die Antwort der dritten Frage vorbereitet.Es fehlt im Programmcode noch das Unterprogramm $test
function test($sample,$g)
{
$merk = FALSE;
for($i=0; $i<count($g); $i++)
{
$zahl = 0;
for($j=0; $j<count($g[0]); $j++)
{
if (in_array($g[$i][$j], $sample, TRUE)) {$zahl++;}
}
if($zahl==count($g[0])) {$merk = TRUE;}
}
return $merk;
}Programmcode 8
Nun ist alles beisammen und die Ausgabe der zweiten Liste in Tabellenform mit den ermittelten Eigenschaften kann erfolgen.| Typ | Anzahl | Kanten | $bit-Eigenschaften | schematische Darstellung |
|---|---|---|---|---|
| 1 | 24 | 1,2,3,4,5,6,7 | Ring | Klick auf eine der linken Zeilen erzeugt die Darstellung des zugehörigen Netzwerk-Typs |
| 2 | 24 | 1,2,3,4,5,6,9 | verzweigt | |
| 3 | 24 | 1,2,3,4,5,6,10 | linear | |
| 4 | 24 | 1,2,3,4,5,7,9 | verzweigt | |
| 5 | 24 | 1,2,3,4,5,7,11 | verzweigt | |
| 6 | 24 | 1,2,3,4,5,8,9 | verzweigt Ring | |
| 7 | 24 | 1,2,3,4,5,8,10 | verzweigt Ring | |
| 8 | 24 | 1,2,3,5,6,7,9 | verzweigt unvollständig Ring | |
| 9 | 24 | 1,2,3,5,6,7,10 | verzweigt unvollständig Ring | |
| 10 | 24 | 1,2,3,5,6,7,11 | verzweigt Ring | |
| 11 | 24 | 1,2,3,5,6,7,12 | verzweigt unvollständig Ring | |
| 12 | 12 | 1,2,3,5,6,8,9 | verzweigt | |
| 13 | 24 | 1,2,3,5,6,8,10 | verzweigt | |
| 14 | 12 | 1,2,3,5,6,8,11 | linear | |
| 15 | 24 | 1,2,3,5,6,9,10 | verzweigt unvollständig Ring | |
| 16 | 24 | 1,2,3,5,6,9,11 | verzweigt | |
| 17 | 24 | 1,2,3,5,6,9,12 | verzweigt unvollständig Ring | |
| 18 | 12 | 1,2,3,5,6,10,11 | linear | |
| 19 | 24 | 1,2,3,5,6,10,12 | verzweigt unvollständig Ring | |
| 20 | 24 | 1,2,3,5,6,11,12 | verzweigt | |
| 21 | 24 | 1,2,3,5,7,8,9 | verzweigt | |
| 22 | 12 | 1,2,3,5,7,8,10 | verzweigt | |
| 23 | 12 | 1,2,3,5,7,8,12 | linear | |
| 24 | 24 | 1,2,3,5,7,9,10 | verzweigt unvollständig Ring | |
| 25 | 12 | 1,2,3,5,7,9,11 | verzweigt | |
| 26 | 24 | 1,2,3,5,7,9,12 | verzweigt unvollständig Ring | |
| 27 | 24 | 1,2,3,5,7,10,12 | verzweigt unvollständig Ring | |
| 28 | 24 | 1,2,3,5,7,11,12 | verzweigt | |
| 29 | 24 | 1,2,3,5,8,9,10 | verzweigt Ring | |
| 30 | 24 | 1,2,3,5,8,9,12 | verzweigt | |
| 31 | 24 | 1,2,3,5,8,10,12 | verzweigt | |
| 32 | 12 | 1,2,3,5,8,11,12 | Ring | |
| 33 | 12 | 1,2,3,6,7,9,10 | verzweigt unvollständig Ring | |
| 34 | 24 | 1,2,3,6,7,9,12 | verzweigt unvollständig Ring | |
| 35 | 24 | 1,2,3,6,7,10,12 | verzweigt unvollständig Ring | |
| 36 | 24 | 1,2,3,6,8,9,12 | verzweigt | |
| 37 | 12 | 1,2,3,6,8,10,12 | verzweigt | |
| 38 | 12 | 1,2,3,7,8,9,12 | linear |
Tabelle 2
Die Antworten auf die dritte Frage ist nun das Zählergebnis der entsprechenden Eigenschaften. $$\rand{\begin{align} \text{Anzahl linearer Netzwerke}&=5 \\ \text{Anzahl verzweigter Netzwerke}&=15 \\ \text{Anzahl geteilter Netzwerke}&=6 \\ \text{Anzahl unvollständiger Netzwerke}&=12\end{align}}$$