1.) Anordnung der Platonischen Körper
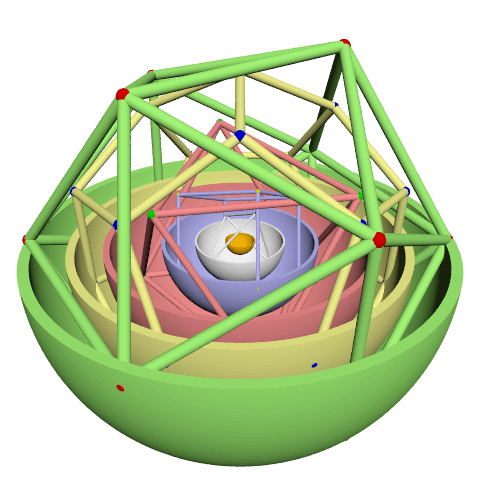
Die beiden oben abgebildeten "Weltmodelle" unterscheiden sich nur in der Anordnung der Platonischen Körper und damit in den inneren Abständen der Sphären.
Die innerste Kugelschale des Merkur und die äußerste Kugelschale des Saturn sind am selben Platz.
Das ist nicht verwunderlich, weil das Verhältnis dieser beiden unabhängig von den inneren Schalenpositionen ist.
Jeder Platonische Körper hat unabhängig von seiner absoluten Größe immer dasselbe Verhältnis der Radien von Umkugel zu Inkugel:
| Körper | Inkugel-
Radius $r_I$ | Umkugel-
Radius $r_U$ | $\displaystyle{\frac{r_U}{r_I}}$ |
|---|
| Tetraeder |
$\frac a{12}\cdot\sqrt{6}$ |
$\frac a4\cdot\sqrt{6}$ |
$3,00000000$ |
| Hexaeder |
$\frac a2$ |
$\frac a2\cdot\sqrt{3}$ |
$1,73205081$ |
| Oktaeder |
$\frac a6\cdot\sqrt{6}$ |
$\frac a2\cdot\sqrt{2}$ |
$1,73205081$ |
| Dodekaeder |
$\frac a2\cdot\sqrt{(25+11\cdot\sqrt{5})/10}$ |
$\frac a4\cdot\sqrt{3}\cdot (1+\sqrt{5})$ |
$1,25840857$ |
| Ikosaeder |
$\frac a{12}\cdot\sqrt{3}\cdot (3+\sqrt{5})$ |
$\frac a4\cdot\sqrt{10+2\cdot\sqrt{5}}$ |
$1,25840857$ |
Tabelle 1
Um eine optimale Zuordnung der Sphären-Verhältnisse zu den Verhältnissen der Planetenbahnen zu erreichend,
bestimmt man zunächst die Bahnverhältnisse der großen Halbachsen der Planeten und ordnet diesen dann passende Körper aus der Tabelle 1 zu:
| Planet | große Halbachse | Verhältnis | Körper |
|---|
| Merkur | 57909175 km | |
| 1,86859733 | Hexaeder oder Oktaeder |
| Venus | 108208930 km |
| 1,38249117 | Dodekaeder oder Ikosaeder |
| Erde | 149597890 km |
| 1,52366213 | Dodekaeder oder Ikosaeder |
| Mars | 227936640 km |
| 3,41503683 | Tetraeder |
| Jupiter | 778412020 km |
| 1,83286661 | Hexaeder oder Oktaeder |
| Saturn | 1426725400 km |
|
Tabelle 2
Bild 3
Damit ergeben sich die auf der Rätselseite unter 1.) gefragten vier besten Anordnungen, die in ihren Verhältniszahlen untereinander völlig gleich sind:
| 1 | 2 | 3 | 4 |
|---|
| Oktaeder | Hexaeder | Oktaeder | Hexaeder |
| Ikosaeder | Ikosaeder | Dodekaeder | Dodekaeder |
| Dodekaeder | Dodekaeder | Ikosaeder | Ikosaeder |
| Tetraeder | Tetraeder | Tetraeder | Tetraeder |
| Hexaeder | Oktaeder | Hexaeder | Oktaeder |
Tabelle 3
wobei die erste Anordnung der
Tabelle 3 im
Bild 2 oben rechts als auch 1596 in dem Buch "Mysterium Cosmographicum" von Kepler gewählt wurde:

|
|
Bild 4
|
Bild 5
|
2.) Optimierung bei dünnen Sphären
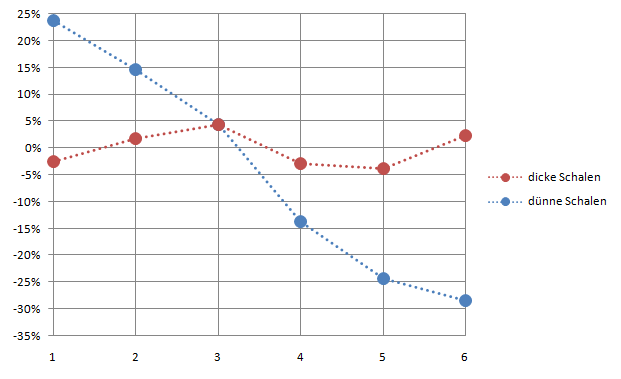
Da es in den Rätselfragen immer nur um relative Abweichungen geht, ist die Größe des Sonnensystems oder des Modells unerheblich.
Man kann alles mit den in
Tabelle 1 und
Tabelle 2 aufgelisteten Verhältniszahlen berechnen.
Das Prinzip der Gegeüberstellung der Verhältnisse wird in der noch nicht optimierten
Tabelle 4 gezeigt:
| Planet | rel. Position
im Sonnensystem | rel. Position
im Modellsystem | Abweichung | Abweichungs-
quadrat |
|---|
| Merkur | 1,00000000 | 1,00000000 | 0,00000000 % | 0,00000000 % |
| Venus | 1,86859733 | 1,73205081 | -7,30743449 % | 0,53398599 % |
| Erde | 2,58331931 | 2,17962758 | -15,62686132 % | 2,44198795 % |
| Mars | 3,93610581 | 2,74286204 | -30,31533778 % | 9,19019705 % |
| Jupiter | 13,44194629 | 8,22858611 | -38,78426582 % | 15,04219275 % |
| Saturn | 24,63729452 | 14,25232922 | -42,15140302 % | 17,76740776 % |
| Summe der Abweichungsquadrate | 44,97577150 % |
Tabelle 4
Dabei startet die Position von Merkur in beiden Modellen mit eins.
Jede weitere Zeile multipliziert die vorangegangene Position mit dem zugehörigen Verhältnisfaktor.
Die dimensionslose relative Abweichung zwischen beiden Modellen wird mit $(r_S-r_M)/r_S$ berechnet und in Prozent ausgegeben.
Dabei ist $r_S$ der Radius im Sonnensystem und $r_M$ der Radius im Modellsystem.
Die letzte Spalte quadriert die Abweichung und zeigt den Wert ebenfalls in Prozent.
Diese letzte Spalte wird aufaddiert und die Summe in der letzten Zeile ausgegeben.
Man sieht, dass die Abweichung bei Null beginnt, aber nach außen deutlich zunimmt.
Durch Verschiebung der Startposition zu höheren Werten kann die Quadratsumme minimiert werden.
Es gibt verschiedene Möglichkeiten für diese Optimierung.
Ich habe mit EXCEL eine Makro-Funktion geschrieben und das Minimum mit dem Solver ermittelt.
Function kepler(start, dicke)
vS = Array( _
1, _
1.86859733366949, _
1.3824911677807, _
1.52366213186563, _
3.41503682777811, _
1.83286660963946)
vM = Array( _
start, _
1.73205080756888, _
1.25840857236482, _
1.25840857236482, _
3, _
1.73205080756888)
rS = 1
rM = 1
minimum = 0
For i = 0 To 5
rS = rS * vS(i)
rM = rM * vM(i)
dM = rM * (1 + dicke)
rM = dM
pM = (rM + dM) / 2
abw = (pM - rS) / rS
abw2 = abw * abw
minimum = minimum + abw2
Next i
kepler = minimum
End Function
Programm-Code 1
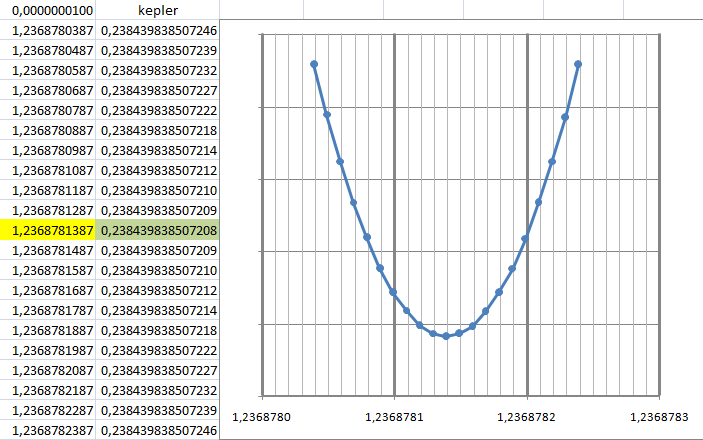
Der Solver liefert mit $dicke=0$ ein Minimum für den Wert $start=1,23687813878365$
Wer nicht mit dem Solver zum Ergebnis kommen will, kann eine einfache Intervallschachtelung von Hand durchführen.
Dazu ist folgendes in das EXCEL-Blatt einzugeben:
Bild 6
Zu Beginn schreibt man in der obersten linken Zelle den Wert $0,1$. Das ist die Schrittweite der darunter befindlichen Eingabewerte.
Die feste Mitte (gelb hinterlegt) wird zu Anfang auf $1$ gesetzt und die Werte oberhalb und unterhalb davon ausgehend mit der Schrittweite automatisch gefüllt.
Die zweite Spalte zeigt das Ergebnis der Funktion in
Programm-Code 1
mit dem ersten Parameter aus der links daneben stehenden Zelle und dem zweiten Parameter gleich Null.
Die beiden Spalten zusammen können als Wertetabelle mit EXCEL grafisch dargestellt werden, wie im
Bild 6 rechts.
Dabei ist das Minimum bei jeder Stufe der Intervallschachtelung deutlich zu erkennen.
Zusätzlich ist eine farbliche Markierung (hier hellgrün) des kleinsten Wertes in der Tabelle mit der bedingten Formatierung noch leichter zu erkennen.
Zwei Schritte sind nun solange zu wiederholen bis das Ergebnis nicht weiter verbessert werden kann:
1.) man überträgt den Wert der Zelle links vom Minimum auf das gelb hinterlegte Feld, dadurch wandert des Minimum dorthin.
2.) man macht in der Zelle ganz oben links den Anfangswert kleiner, an einfachsten durch Einfügen von Null hinter dem Komma.
Dadurch spreizt sich der Bereich und meistens erscheint ein Minimum an einer anderen Stelle.
Nach sieben Schritten sieht das Tabellenblatt dann so aus wie in
Bild 6.
Auch hierbei kommt man wie der Solver zum gleichen Minimum,
und der zugehörige Startwert kann nun für das Modellsystem in die
Tabelle 4 statt der eins eingegeben werden.
Das erzeugt eine Ergebnistabelle für die Rätselfrage 2.):
| Planet | rel. Position
im Sonnensystem | rel. Position
im Modellsystem | Abweichung | Abweichungs-
quadrat |
|---|
| Merkur | 1,00000000 | 1,23687814 | 23,68781388 % | 5,61112526 % |
| Venus | 1,86859733 | 2,14233578 | 14,64940790 % | 2,14605152 % |
| Erde | 2,58331931 | 2,69593371 | 4,35929074 % | 0,19003416 % |
| Mars | 3,93610581 | 3,39258609 | -13,80856469 % | 1,90676459 % |
| Jupiter | 13,44194629 | 10,17775827 | -24,28359664 % | 5,89693066 % |
| Saturn | 24,63729452 | 17,62839443 | -28,44833504 % | 8,09307766 % |
| Summe der Abweichungsquadrate | 23,84398385 % |
Tabelle 5
3.) Optimierung bei dicken Sphären
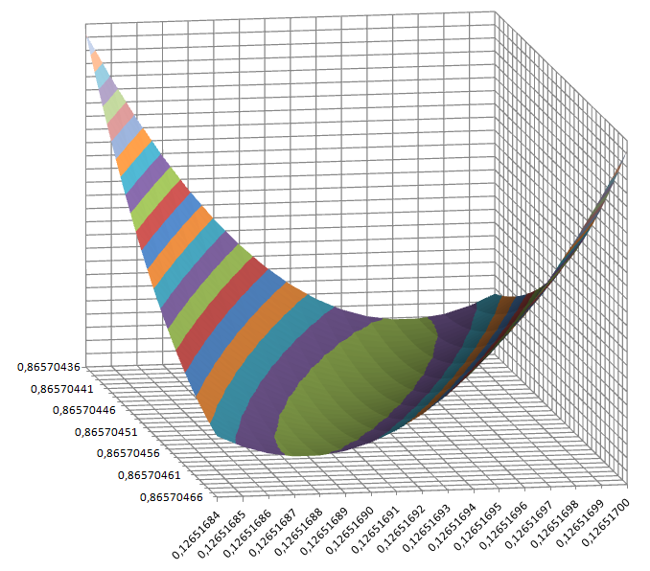
Wenn man das gleiche EXCEL-Programm nun mit der Dicke als zweite Variable vom Solver berechnen lässt ergibt sich:
$$
Startwert=0,865704514 \\
Schalendicke=12,65169242\,\%
$$
Ohne Solver läuft es mit der Intervallschachtelung auf das Gleiche hinaus wie oben beschrieben, nur in zwei Dimensionen.
Statt eines parabelförmigen Kurvenverlaufs kann EXCEL eine Flächendarstellung erzeugen:
Bild 7
Die gefundenen Werte in die Tabelle eingefügt zeigt die Lösung der Rätselfrage 3.):
| Planet | rel. Position
im Sonnensystem | rel. Position
im Modellsystem | Abweichung | Abweichungs-
quadrat |
|---|
| Merkur | 1,00000000 | 0,97523079 | -2,47692136 % | 0,06135139 % |
| Venus | 1,86859733 | 1,90285524 | 1,83334885 % | 0,03361168 % |
| Erde | 2,58331931 | 2,69752290 | 4,42080799 % | 0,19543543 % |
| Mars | 3,93610581 | 3,82405851 | -2,84665362 % | 0,08103437 % |
| Jupiter | 13,44194629 | 12,92359989 | -3,85618563 % | 0,14870168 % |
| Saturn | 24,63729452 | 25,21632841 | 2,35023325 % | 0,05523596 % |
| Summe der Abweichungsquadrate | 0,57537052 % |
Tabelle 6
4.) Zusammenfassung
Bild 8
5.) geschichtlich Wertung
Kepler gab sein Modell mit Platonischen Körpern auf, als die genaueren Beobachtungen von Tycho Brahe ihm zur Verfügung standen.
Daraus konnte er ableiten, dass die Planetenbahnen keine Kreise sondern Ellipsen waren.
Spätestens mit der Endeckung von Uranus im Jahre 1781 durch Friedrich Wilhelm Herschel wurde das System mit Platonischen Körpern endgültig gestürzt.
Ein anderes System, 1766 von Johann Daniel Titius aufgestellt,
nahm mit Begeisterung den neuen Planeten auf, weil er ideal in die sogenannte Titius-Bode-Reihe passte.
Der Makel dieses Systems liegt in der Abwesenheit eines Planeten zwischen Mars und Jupiter, jedoch nach intensiver Suche fand man dort 1801 den Kleinplaneten Ceres.
Die Freude über die passende Erweiterung durch Uranus wurde aber schon in Jahre 1846 sehr getrübt
weil der neu entdeckte Planet Neptun sich nicht an das System von Bode anpassen ließ.
Der später gefundene Pluto kann aber den Platz von Neptun in der Reihe ganz gut einnehmen und so wurde Neptun als Eindringling bezeichnet,
der zudem sich schon als fremdartig durch seine um ihn kreisende Mondbahnen zeigte.
Später fand man auch, dass seine eigenen Rotationsachse so wie die Mondbahnen fast 90 Grad gegen die Ekliptik geneigt sind.
Die Titius-Bode-Reihe ist inzwischen nicht mehr als eine Gesetzmäßigkeit anerkannt, obwohl auf 27 extrasolaren Planetensystemen angewandt, eine Übereinstimmung von 96% gefunden wurde.