Preisrätsel Oktober 2019
Keplers "Mysterium Cosmographicum"
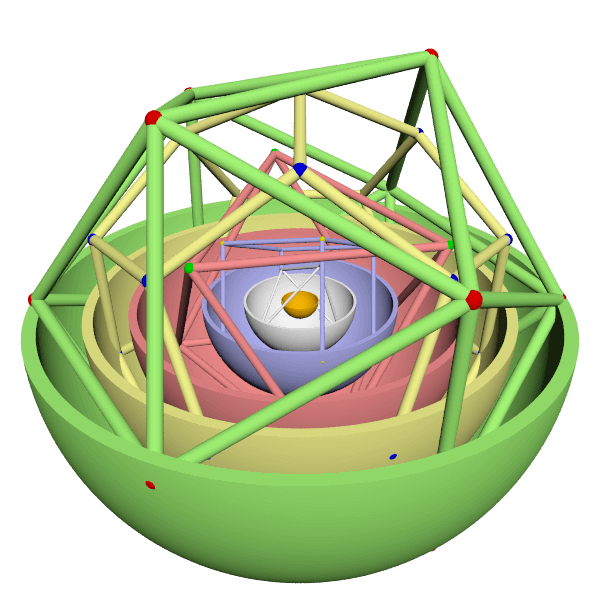
Keplers "Mysterium Cosmographicum"

In seinem 1596 veröffentlichten Buch Mysterium Cosmographicum (Das Weltgeheimnis) stellte Kepler ein Modell des damals bekannten Sonnensystems
mit den Planetensphären Merkur, Venus, Erde, Mars, Jupiter und Saturn vor.
Die Kugelschalen, ähnlich wie auf dem obigen Bild, werden durch die fünf platonischen Körper so auf Abstand gehalten, dass die Umkugel eines inneren Körpers gleich der Inkugel des nach außen folgenden Körpers war. Dadurch ergaben sich feste Verhältnisse aller Planetensphären zueinander.
Noch bessere Übereinstimmung mit der Realität bekommt man, wenn die Sphären nicht unendlich dünn, sondern eine Dicke aufweisen, die einem bestimmten Prozentsatz des Radius entsprechen, wie im Bild oben zu sehen ist.
Bei fünf Platonischen Körpern gibt es 5 ! = 120 Möglichkeiten der Anordnung. Das dabei auch einige sehr gut die tatsächlichen Verhältnisse der heute genauer bekannten großen Halbachsen der Planetenbahnen treffen ist trotzdem verwunderlich.
Rätselaufgabe:
1.) Welche vier Anordnungen der Platonischen Körper von innen nach außen treffen am besten die wirklichen Verhältnisse der Planetenbahnen?
2.) Das Modell mit unendlich dünnen Kugelschalen kann so skaliert werden, dass die Sphären im Vergleich mit den wirklichen großen Halbachsen der Planeten optimal übereinstimmen. Das soll dann der Fall sein, wenn die Quadrate der relativen Abweichungen (riM - riS) / riS aufsummiert minimal werden. Wie groß sind dabei diese Abweichungen in Prozent für die sechs Planeten?
riM sind die Sphärenradien im Modellsystem
riS sind die skalierten großen Halbachsen im Sonnensystem
i ist der Laufindex von 0 bis 5 durch die Planeten
3.) Wenn man mit dicken Kugelschalen, in deren Mitte die Position der Planeten angenommen wird, die gleiche Art der Skalierung wie unter 2.) vornimmt, jetzt aber mit einem optimierten Prozentsatz des Radius für die Dicke der Sphären, wie groß muss dieser Prozentsatz sein und wie groß sind dabei die Abweichungen in Prozent für die sechs Planeten dann?
Die drei besten richtigen Antworten gewinnen.
Viel Spaß bei der Beschäftigung mit diesem Rätsel.
Die Kugelschalen, ähnlich wie auf dem obigen Bild, werden durch die fünf platonischen Körper so auf Abstand gehalten, dass die Umkugel eines inneren Körpers gleich der Inkugel des nach außen folgenden Körpers war. Dadurch ergaben sich feste Verhältnisse aller Planetensphären zueinander.
Noch bessere Übereinstimmung mit der Realität bekommt man, wenn die Sphären nicht unendlich dünn, sondern eine Dicke aufweisen, die einem bestimmten Prozentsatz des Radius entsprechen, wie im Bild oben zu sehen ist.
Bei fünf Platonischen Körpern gibt es 5 ! = 120 Möglichkeiten der Anordnung. Das dabei auch einige sehr gut die tatsächlichen Verhältnisse der heute genauer bekannten großen Halbachsen der Planetenbahnen treffen ist trotzdem verwunderlich.
Rätselaufgabe:
1.) Welche vier Anordnungen der Platonischen Körper von innen nach außen treffen am besten die wirklichen Verhältnisse der Planetenbahnen?
2.) Das Modell mit unendlich dünnen Kugelschalen kann so skaliert werden, dass die Sphären im Vergleich mit den wirklichen großen Halbachsen der Planeten optimal übereinstimmen. Das soll dann der Fall sein, wenn die Quadrate der relativen Abweichungen (riM - riS) / riS aufsummiert minimal werden. Wie groß sind dabei diese Abweichungen in Prozent für die sechs Planeten?
riM sind die Sphärenradien im Modellsystem
riS sind die skalierten großen Halbachsen im Sonnensystem
i ist der Laufindex von 0 bis 5 durch die Planeten
3.) Wenn man mit dicken Kugelschalen, in deren Mitte die Position der Planeten angenommen wird, die gleiche Art der Skalierung wie unter 2.) vornimmt, jetzt aber mit einem optimierten Prozentsatz des Radius für die Dicke der Sphären, wie groß muss dieser Prozentsatz sein und wie groß sind dabei die Abweichungen in Prozent für die sechs Planeten dann?
Die drei besten richtigen Antworten gewinnen.
Viel Spaß bei der Beschäftigung mit diesem Rätsel.