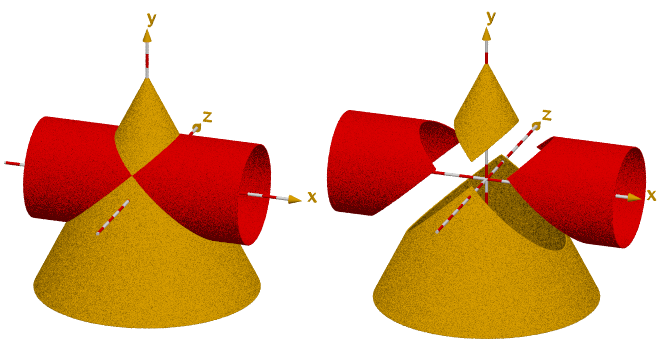
1.) Auflistung und Berechnung der Konstanten bei diesem Rätsel
$$\begin{alignat}{3}
\textbf{gegeben:} \\
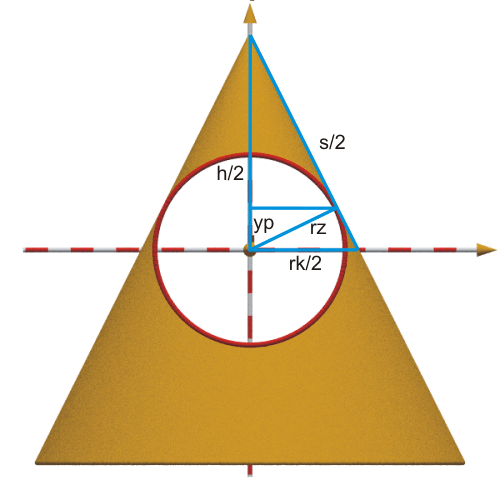
& \text{Höhe von Zylinder und Kegel:}& h & =& 1,0000000000& \;m \\
& \text{Radius der Kreiskegel-Grundfläche:}& rk = h/2 & =& 0,5000000000& \;m \\
\\
\textbf{berechnet:} \\
& \text{Kantenlänge des Kegel:}& s = \sqrt{h^2 + rk^2}=\frac h2 \cdot\sqrt{5}& =& 1,1180339887& \;m \\
& \text{Zylinder-Radius:}& rz = \frac{h \cdot rk}{2 \cdot s}=\frac {h\cdot \sqrt{5}}{10}& =& 0,2236067977& \;m \\
& \text{y-Koordinate vom Treffpunkt der Teile:}& yp = \frac{rk \cdot rz}{s}=\frac h{10}& =& 0,1000000000& \;m \\
& \text{Umfang des Zylinders: }& Uz = 2\cdot \pi \cdot rz& =& 1,4049629462& \;m \\
& \text{Umfang der Kegel-Grundfläche:}& Uk = 2\cdot \pi \cdot rk& =& 3,1415926536& \;m \\
& \text{vollständige Mantelfläche des Zylinder:}& MZ = h \cdot 2 \cdot \pi \cdot rz& =& 1,4049629462& \;m^2 \\
& \text{vollständige Mantelfläche des Kegels:}& MK = s\cdot \pi \cdot rk& =& 1,7562036828& \;m^2 \\
& \text{Mittelpunktswinkel des Kegel-Mantels:}& \alpha = rk/s\cdot 360°& =& 160,9968943800& °
\end{alignat}$$
|
Herleitung
für die Kantenlänge
$$
\left(\frac s2\right)^2 =\left(\frac h2\right)^2 + \left(\frac {rk}2\right)^2 \\
s = \sqrt{h^2 + rk^2}
$$
für den Zylinder-Radius
$$
rz:\frac{rk}2=\frac h2:\frac s2 \\
rz=\frac{h\cdot rk}{2\cdot s}
$$
für die y-Koordinate
$$
yp:rz=\frac {rk}2:\frac s2 \\
yp=\frac{rk \cdot rz}{s}
$$
|
2.) Lösungsmethode: wiegen und messen

|
Bild 2
|
Nicht die eleganteste Methode aber eine Methode:
man schneidet entsprechend Bild 2 aus Sperrholz oder Kunststoff ein vergrößertes Modell aus, wiegt zunächst die beiden Teile ohne die Ausschnitte im Inneren
und entfernt anschließend die inneren Flächen, sodass sowohl der Kegelmantel links als auch der Zylindermantel rechts in jeweils zwei Teile zerfallen.
Diese vier Teile wiegt man ebenfalls und kann nun mit den 6 Gewichten die Frage nach den Flächen beantworten.
$$\begin{alignat}{1}
k_{gesamt}=& \text{ Gesamtgewicht des Kegelmantels} \\
z_{gesamt}=& \text{ Gesamtgewicht des Zylindermantels} \\
k_{oben}=& \text{ oberes Teilgewicht des Kegelmantels} \\
k_{unten}=& \text{ unteres Teilgewicht des Kegelmantels} \\
z_{rechts}=& \text{ rechtes Teilgewicht des Zylindermantels} \\
z_{links}=& \text{ linkes Teilgewicht des Zylindermantels} \\
\\
MK_{oben}=& \text{ obere Teilfläche des Kegelmantels } \\
MK_{unten}=& \text{ untere Teilfläche des Kegelmantels } \\
MZ_{rechts}=& \text{ rechte Teilfläche des Zylindermantels } \\
MZ_{links}=& \text{ linke Teilfläche des Zylindermantels } \\
\\
MK_{oben}=& \frac{k_{oben}}{k_{gesamt}}\cdot MK \\
MK_{unten}=& \frac{k_{unten}}{k_{gesamt}}\cdot MK \\
MZ_{rechts}=& \frac{z_{rechts}}{z_{gesamt}}\cdot MZ \\
MZ_{links}=& \frac{z_{links}}{z_{gesamt}}\cdot MZ
\end{alignat}$$
Zuletzt müssen noch die Längen der Schweißnähte am Modell gemessen werden und mit den bekannten Längen aus obiger Liste ins richtige Verhältnis gesetzt werden.
Wenn alles mit großer Sorgfalt bestimmt wird ist eine Lösung mit etwa 1% Genauigkeit eine akzeptable Lösung.
3.) Lösungsmethode: Statistik beim berechnen des Kegelmantels
Man kann eine große Zahl von zufällig bestimmten Punkten auf der Oberfläche der beiden Mantelflächen erzeugen und für jeden Punkt fragen,
ob er sich im einen Bereich, im anderen Bereich oder in der Überlappung der Körper befindet und entsprechend der Antwort einen Zähler zum entsprechenden Bereich erhöhen.
Mit einer sehr großen Anzahl solcher Punkte bekommt man ein aussagefähiges ganzzahliges Verhältnis der 3 Bereiche für jeden Mantel.
Mit der Kenntnis der Gesamtfläche aus Punkt 1 ist dann das Ergebnis zu errechnen.
Die Methode scheint schwierig, ist sie aber nicht.
Das einzige Problem dabei ist die erforderliche Rechenzeit bei sehr großen Mengen an Punkten.
Die Bilder 1 und 2 sind übrigens mit jeweils einer Million Punkten für beide Mantelflächen erzeugt worden.
Die heutigen PCs sind schnell genug, um auch noch größere Zahlen zu verarbeiten.
Das nötige Programm 1 ist absolut simpel:
Für den Kegel werden zwei Zufallszahlen im Bereich $±0,5$ erzeugt, die ein Quadrat um die Grundfläche gleichmäßig abdecken.
Diese werden als x- und z-Koordinate angesehen (Zeile 9 und 10) und nur verwendet, wenn der Radius des Grundkreises nicht überschritten wird.
Das ist in 78,54 % der Fall. Wenn der so zufällig erzeugte aktuelle Kegelradius $akr$ zu groß ist werden neue Zufallszahlen erzeugt (Zeile 12 und 13).
Da nun ein Radius bekannt ist (Zeile 15) kann daraus auf die Höhe des Punktes geschlossen werden (Zeile 16), denn er muss ja auf der Oberfläche des Kegels liegen.
Somit erhält man die y-Koordinate des Punktes.
Nun wird aus y und z ein Radiuswert gebildet, und wenn dieser kleiner als der Zylinderradius ist (Zeile 17), liegt der Punkt in der Überlappung beider Körper
und muss daher zum ausgeschnittenen Teil des Kegelmantels zählen.
Anderenfalls ist er Teil der Mantelfläche und der y-Wert entscheidet (Zeile 18), ob er im oberen Teil bei $y > yp$ oder im unteren Teil bei $y < yp$ gezählt wird.
Das gesamte in PHP geschriebene Programm, was auch hier auf dieser Seite jetzt läuft und die unten folgende Tabelle erzeugt, sieht so aus:
function kegel($n)
{
global $yp, $MK, $rz;
$fein = 1000000000;
$c1 = 0;
$c2 = 0;
$start = microtime(true);
for($i=1; $i<=$n; $i++){
$x = mt_rand(0,$fein)/$fein-0.5;
$z = mt_rand(0,$fein)/$fein-0.5;
while($x*$x+$z*$z > 0.25){
$x = mt_rand(0,$fein)/$fein-0.5;
$z = mt_rand(0,$fein)/$fein-0.5;
}
$akr = sqrt($x*$x + $z*$z);
$y = 0.5-2*$akr;
if($y*$y + $z*$z > $rz*$rz){
if($y > $yp){ $c1++; } else { $c2++; }
}
}
$end = microtime(true);
$res=[$MK*$c1/$n,$MK*$c2/$n,$end - $start];
return $res;
}
Programm 1
| Flächenteile vom Kegelmantel |
| n | MKoben | MKunten | Zeit in s | Fehler |
| 100 | 0,2107444419 | 1,1766564674 | 0,0000529289 | 10,8702874940% |
| 10000 | 0,1828208034 | 1,1483815882 | 0,0030620098 | 1,7408368384% |
| 1000000 | 0,1760242951 | 1,1485080348 | 0,3640329838 | -0,1758827752% |
| ∞ | 0,1767871794 | 1,1475926988 | ∞ | 0,0000000000% |
Tabelle 1
Die letzte Zeile der Tabelle wurde nicht mit diesem Programm errechnet sondern mit der nächsten Lösungsmethode nur zum Vergleich der Genauigkeit hinzugefügt.
Die Werte in der Tabelle werden bei jedem Start der Internetseite neu berechnet und sind jedes mal verschieden, eben statistisch verteilt.
4.) Lösungsmethode: Statistik beim berechnen des Zylindermantels
Das Berechnen der Flächen beim Zylindermantel läuft im Programm 2 sehr ähnlich ab:
Zunächst wird eine x-Koordinate im Bereich $±0,5$ erzeugt (Zeile 9) und ein Winkel zwischen $0$ und $2π$ (Zeile 10).
Damit ist der gesamte Zylindermantel gleichmäßig abgedeckt.
Daraus können sofort die y- und z-Koordinaten berechnet werden (Zeile 11 und 12).
In der Höhe von y ist der Kegelradius festgelegt (Zeile 13).
Nur wenn der aus x und z gebildete Radius größer ist (Zeile 14) befinden wir uns außerhalb der Überschneidung beider Körper
und nun ist nur noch zwischen rechts bei $x > 0$ und links bei $x < 0$ zu unterscheiden (Zeile 15).
function zylinder($n)
{
global $MZ;
$fein = 1000000000;
$rz = sqrt(5)/10;
$c1 = 0; $c2 = 0;
$start = microtime(true);
for($i=1; $i<=$n; $i++){
$x = mt_rand(0,$fein)/$fein-0.5;
$w = mt_rand(0,$fein)/$fein*2*pi();
$y = sin($w)*$rz;
$z = cos($w)*$rz;
$akr = (0.5-$y)/2;
if($x*$x + $z*$z > $akr*$akr){
if($x > 0){ $c1++; } else { $c2++; }
}
}
$end = microtime(true);
$res=[$MZ*$c1/$n,$MZ*$c2/$n,$end - $start];
return $res;
}
Programm 2
| Flächenteile vom Zylindermantel |
| n | MZrechts | MZlinks | Zeit in s | Fehler |
| 100 | 0,4495881428 | 0,4214888839 | 0,0000858307 | -4,5116081759% |
| 10000 | 0,4556294835 | 0,4637782685 | 0,0033879280 | 0,7864574350% |
| 1000000 | 0,4560341128 | 0,4564050230 | 0,3377478123 | 0,0225503004% |
| ∞ | 0,4561167122 | 0,4561167122 | ∞ | 0,0000000000% |
Tabelle 2
Die statistische Methode ist bei mir immer die erste, um einen Überblick über das Problem zu bekommen.
Sie liefert zuverlässige Zahlenwerte, und ein Verrechnen, wie bei der nun folgenden Integralmethode ist praktisch ausgeschlossen, da nur gezählt wird.
Die Genauigkeit ist für die meisten praktische Fälle auch ausreichend.
Eine Bestimmung der Länge der Schweißnähte ist allerdings nicht möglich.
5.) Lösungsmethode: Integral beim Zylindermantel
Um die Konturen der Abwicklung des Zylindermantels zu berechnen
muss man anders als bei der statistischen Methode nicht durch Zufall Punkte in der Fläche festlegen sondern genau auf die Grenzen zielen.
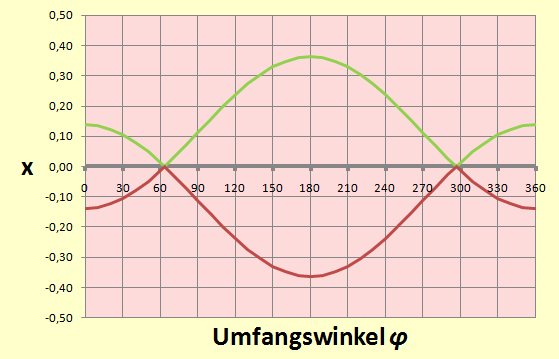
Wenn man Bild 2 rechts betrachtet, erkennt man im Verlauf des Umfangs (horizontal) unterschiedliche Höhen (vertikal).
Den Verlauf des Umfangs kann man mit einem ansteigenden Winkel von 0° bis 360° oder $0$ bis $2π$ beschreiben, die Höhe ist die x-Koordinate der Grenzpunkte.
Also bildet man einen Funktionsverlauf $x(\varphi)$ der Konturen in x-Richtung über den Umfangswinkel $\varphi$:
$$
\eqalign{
z(\varphi) = rz \cdot\sin \varphi \\
y(\varphi) = rz \cdot\cos \varphi \\
akr(\varphi) = (h/2-y(\varphi))/2 \\
x(\varphi) = \pm\sqrt{akr^2(\varphi)-z^2(\varphi)}
}\tag{1}
$$
Die Koordinaten der Grenzpunkte sind damit leicht zu berechnen.
Eine Wertetabelle mit EXCEL lässt das folgende Bild 3 entstehen:
Bild 3
Dass sich gleich zwei Kurvenverläufe ergeben liegt an der Wurzel, die ein positives und ein negatives Vorzeichen aufweist.
Das ist aber auch erwünscht, denn genau so sieht ja auch der Verlauf der Kontur in Bild 2 rechts aus.
Einsetzen und weiteres Vereinfachen führt zu folgenden Zeilen:
$$
x(\varphi)=\pm\sqrt{\left(h^2/4-h\cdot y(\varphi)+y^2(\varphi)\right)/4-z^2(\varphi)} \\
=\pm\frac12\cdot\sqrt{h^2/4-h \cdot y(\varphi)+y^2(\varphi)-4\cdot z^2(\varphi)} \\
=\pm\frac12\cdot\sqrt{h^2/4-h \cdot rz \cdot\cos \varphi+(rz \cdot\cos \varphi)^2-4\cdot (rz \cdot\sin \varphi)^2} \\
=\pm\frac h2\cdot\sqrt{\frac{1}{4}- \frac {\sqrt{5}}{10} \cdot \cos \varphi+\frac{\cos^2\varphi}{20}-\frac{\sin^2\varphi}{5}} \\
=\pm\frac h2\cdot\sqrt{\frac{1}{4}- \frac {\sqrt{5}}{10} \cdot \cos \varphi+\frac{\cos^2\varphi}{20}-\frac{1-\cos^2\varphi}{5}} \\
=\pm\frac h2\cdot\sqrt{\frac14-\frac15- \frac {\sqrt{5}}{10} \cdot \cos \varphi+\left(\frac1{20}+\frac15\right)\cdot\cos^2\varphi} \\
=\pm\frac h2\cdot\sqrt{\frac{5}{100}- \frac {\sqrt{5}}{10} \cdot \cos \varphi + \frac{\cos^2\varphi}{4}} \\
=\pm\frac h2\cdot\sqrt{\left(\frac{\sqrt{5}}{10}\right)^2-2\cdot \frac {\sqrt{5}}{10} \cdot \frac{\cos \varphi}2 + \left(\frac{\cos\varphi}{2}\right)^2} \\
=\pm\frac h2\cdot\sqrt{ \left(\frac {\sqrt{5}}{10} - \frac{\cos \varphi}2 \right)^2}
$$
$$
=\pm \frac h4\cdot\left | \frac {\sqrt{5}}{5} - \cos \varphi \right | \tag{2}
$$
Die gesuchten Flächen $MZ_{rechts}$ und $MZ_{links}$ sind gleich groß.
Sie berechnen sich mit
$$
MZ_{rechts}=MZ_{links}=\frac{MZ}2-\frac {rz\cdot h}4\cdot\intop_0^{2\pi}\left | \frac {\sqrt{5}}{5} - \cos \varphi \right |d\varphi
$$
Der Faktor $rz$ ist hinzugekommen weil die Integration nur bis $2\pi$ geht und nicht über den Umfang $2\pi\cdot rz$.
Zur Vermeidung von Betragsbildung wird das Integral ohne Betragsstriche aufgeteilt in zwei Winkelbereiche:
- 1. Bereich: von $0$ bis $\varphi_0$ mit negativem Vorzeichen
- 2. Bereich: von $\varphi_0$ bis $\pi$ mit positivem Vorzeichen
und der noch fehlende Bereich bis $2\pi$ wird wegen der Symmetrie durch Verdopplung der beiden anderen ersetzt:
$$
\intop_0^{2\pi}\left | \frac {\sqrt{5}}{5} - \cos \varphi \right |d\varphi=2\cdot\left(-\intop_0^{\varphi_0}\frac {\sqrt{5}}{5}-\cos \varphi \;d\varphi + \intop_{\varphi_0}^{\pi}\frac {\sqrt{5}}{5}-\cos \varphi \;d\varphi\right)
$$
Die Zwischengrenze $\varphi_0$ liegt an dem Punkt, bei dem der Funktionswert $x(\varphi)$ gleich Null ist bzw. ohne Betragsstriche das Vorzeichen wechselt:
$$
x(\varphi_0)=\frac14\left(\frac {\sqrt{5}}{5} - \cos \varphi_0\right)=0 \\
\frac {\sqrt{5}}{5}=\cos \varphi_0 \\
\varphi_0=\arccos\left(\frac {\sqrt{5}}{5}\right)=\arctan(2)=1,1071487178=63,4349488229°
$$
Jetzt werden die beiden Integrale der Bereiche berechnet:
$$
I_1= \intop_0^{\varphi_0}\frac {\sqrt{5}}{5}-\cos \varphi \;d\varphi =\frac{x}{\sqrt{5}}-\sin(x)\Bigg |_0^{\varphi_0} \\
I_1=\arctan(2)/\sqrt{5}-\sin(\arctan(2))=-0,3992952322\\
I_2= \intop_{\varphi_0}^{\pi}\frac {\sqrt{5}}{5}-\cos \varphi \;d\varphi =\frac{x}{\sqrt{5}}-\sin(x)\Bigg |_{\varphi_0}^{\pi} \\
I_2=\pi/\sqrt{5}-\arctan(2)/\sqrt{5}+\sin(\arctan(2))=1,8042581784\\
$$
Das Ergebnis zusammengefasst:
$$\rand{
MZ_{rechts}=MZ_{links}=\frac{MZ}2-\frac {rz\cdot h}4\cdot 2\cdot(-I1+I2)=0,4561167122\;m^2
}$$
6.) Lösungsmethode: Integral beim Kegelmantel
Der Verlauf der Berechnung ist dem des Zylindermantels ähnlich.
Zunächst ist das Ziel, die Konturen als Randfunktionen $y(\omega)$ zu bestimmen.
Dabei ist $y$ die Höhe (aber noch nicht die schräge Kegelkante) und $\omega$ der Umlaufwinkel um den Bodenkreis.
Auch wird erst einmal eine kartesische Darstellung erzeugt, die dann später in Polarkoordinaten umgewandelt wird.
$$
akr(\omega) = (h/2-y(\omega))/2 \\
z(\omega) = akr(\omega)\cdot\cos\omega \\
rz^2 = z(\omega)^2 + y(\omega)^2 \\
y(\omega)^2\cdot\left(1+\frac{\cos^2\omega}4\right)-y(\omega)\cdot\left(h\cdot\frac{\cos^2\omega}4\right)+\frac{\cos^2\omega}4\cdot \frac{h^2}4-rz^2=0
$$
Das ist eine quadratische Gleichung für $y(\omega)$.
Die Lösung ist:
$$
\tone{y(\omega) = -\frac {b\pm\sqrt{b^2-4ac}}{2a}} \\
\text{mit} \quad
\tone{a = 1-\frac{\cos^2\omega}4} \quad \text{und} \quad
\tone{b = \frac h4 \cdot\cos^2\omega} \quad \text{und} \quad
\tone{c = h^2\cdot\left(\frac{\cos^2\omega}{16}-\frac1{20}\right)} \\
y(\omega) = h\cdot\frac{1/2\cdot\cos^2\omega\pm2/\sqrt{5}\cdot|\sin\omega|}{4+\cos^2\omega}
$$
Der Funktionsverlauf erzeugt aus einer Wertetabelle mit EXCEL sieht so aus:
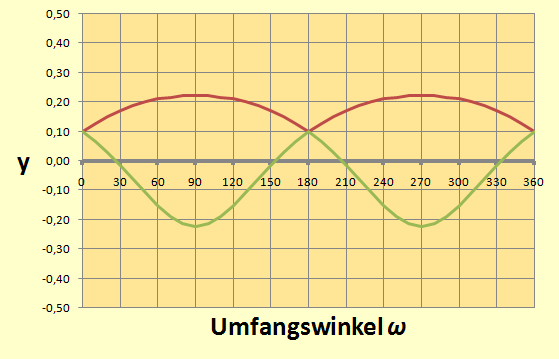
|
Bild 4
Auch in Bild 4 gibt es zwei Konturverläufe und man erkennt schon Ähnlichkeiten mit der Abwicklung des Kegelmantels.
Wichtig ist auch, dass es reicht, den Winkelbereich von $0$ bis $\pi/2$ zu berechnen, denn der gesamte Bereich ist aus Symmetriegründen das vierfache.
Das erlaubt zudem, die Betragsbildung beim Sinus wegzulassen und vereinfacht die Berechnung.
Um von der karthesischen Darstellung zur echten Flächenform zu gelangen sind mehrere Schritte erforderlich:
- Bildung eines Integrals in Polarkoordinaten über die Funktion $r(\omega)$, um zu einer Kreisausschnittsfläche mit variierendem Radius zu gelangen
- Umwandlung der Funktion $y(\omega)$ in die Längenfunktion $r(\omega)$ die den Abstand auf dem Kegelmantel von der Spitze aus angibt, also den variierenden Radius.
- Skalierung vom Winkel $\omega$ auf den Mittelpunktswinkel $\alpha$ (Achtung: beide im gleichen Winkelmaß)
Die Fläche eines Kreisausschnitts, in diesem Fall ein Viertelkreis, ist
$$
A=\intop_0^{\pi/2}\frac12\cdot r(\omega)^2\;d\omega
$$
Dabei ist
$$
r(\omega)=\frac sh \cdot \left(\frac h2 - y(\omega)\right)
$$
Die gesuchten Teilflächen des Kegelmantels sind dann
$$
MK_{oben}= \frac {\alpha}{\pi/2}\cdot s^2 \cdot\intop_0^{\pi/2} \frac12\cdot\left(\frac12 - \frac{1/2\cdot\cos^2\omega + 2/\sqrt{5}\cdot\sin\omega}{4+\cos^2\omega}\right)^2\;d\omega \\
MK_{unten}=MK-\frac {\alpha}{\pi/2}\cdot s^2 \cdot \intop_0^{\pi/2} \frac12\cdot\left(\frac12 - \frac{1/2\cdot\cos^2\omega - 2/\sqrt{5}\cdot\sin\omega}{4+\cos^2\omega}\right)^2\;d\omega \\
$$
Die Berechnung der Integrale kann man dem Rechner überlassen (oder zur Übung von Hand durchführen).
Dazu ist der kostenlose
Integralrechner geeignet, dem man die Zeile
1/2*(1/2-(1/2*cos(x)^2+2/sqrt(5)*sin(x))/(4+cos(x)^2))^2
für das erste Integral $I_1$ und
1/2*(1/2-(1/2*cos(x)^2-2/sqrt(5)*sin(x))/(4+cos(x)^2))^2
für das zweite Integral $I_2$
vorgeben kann. Die Grenzen
pi/2
und
0 müssen bei den Optionen eingetragen werden.
Das Ergebnis ist dann:
$$
I_1=-\frac{10\arctan(\frac12)-5\pi+4}{8{\cdot}5^\frac{3}{2}}=0,0790616302 \\
I_2=\frac{10\arctan(\frac12)+5\pi+4}{8{\cdot}5^\frac32}=0,2721791064 \\
$$
Mit dem Vorfaktor $v=\frac {\alpha}{\pi/2}\cdot s^2=2,2360679775\;m^2$
ist das gesuchte Ergebnis
$$\rand{\begin{alignat}{2}
MK_{oben} & =& v\cdot I_1 =& 0,1767871794\;m^2 \\
MK_{unten} & =& MK-v\cdot I_2 =& 1,1475926988\;m^2
\end{alignat}}$$
7.) die Länge der Schweißnähte
Die zum Aufwickeln und Verbinden der Abwicklungen nötigen Schweißnähte sind sehr einfach zu berechnen.
Für den Kegel ist die gesamte Kantenlänge zu verschweißen:
$$\sand{
Naht_{Kegelmantel}=s=1,1180339887\;m
}$$
Für das Aufwickeln und Verbinden des Zylindermantels ist aus der Höhe eine Aussparung heraus zurechnen.
Es ist der x-Wert bei $\varphi=0$ von der Mitte aus in beiden Richtungen abzuziehen.
Der Wert kann von der Zeile (2) übernommen werden:
$$
x(\varphi)=\pm \frac h4\cdot\left | \frac {\sqrt{5}}{5} - \cos \varphi \right | \\
\sand{Naht_{Zylindermantel}=h-2\cdot x(0)=0,7236067977\;m}
$$
Jetzt geht es um das Zusammenfügen der vier Teile.
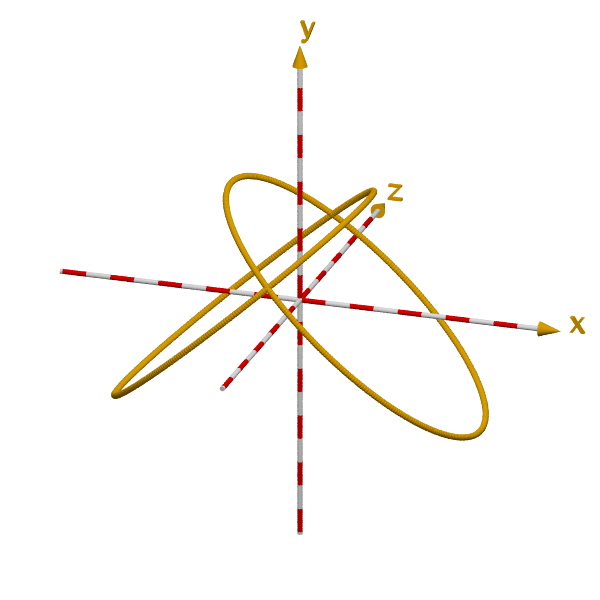
Die 3-dimensionale Lage von 2 mal 360 Schweißpunkten, die als kleine Kugeln Linien bilden, ist in Bild 5 zu sehen.
Bild 5
Darauf ist zu erkennen, dass sich zwei Ellipsen bilden, die die Grenzen der vier Teile markieren.
Die Koordinaten der Punkte lassen sich einfach berechnen, indem man in
die bekannten Gleichungen aus Zeilengruppe (1) bestimmte Winkelwerte eingibt.
Um den Ellipsenumfang berechnen zu können sind nur die kleine und große Achse erforderlich.
Also sucht man nach den vier Punkten, die als Endpunkte dieser Strecken in Frage kommen.
Das ist der Fall bei den Winkeln 0°, 90°, 180° und 270° für $\varphi$
Die folgende Tabelle 3 zeigt die Koordinaten bei diesen Winkeln für die rechte Ellipse im Bild 5.
| φ | x(φ) | y(φ) | z(φ) |
|---|
| 0 | -0,1381966011 | 0,2236067977 | 0,0000000000 |
| 90 | 0,1118033989 | 0,0000000000 | 0,2236067977 |
| 180 | 0,3618033989 | -0,2236067977 | 0,0000000000 |
| 270 | 0,1118033989 | 0,0000000000 | -0,2236067977 |
Tabelle 3
Der räumliche Abstand zwischen zwei Punkten ist
$$
d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}
$$
Die beiden Halbachsen der Ellipse sind dann
$$
a=\frac12\cdot\sqrt{(x(0)-x(180))^2+(y(0)-y(180))^2+(z(0)-z(180))^2}=0,3354101966\;m \\
b=\frac12\cdot\sqrt{(x(90)-x(270))^2+(y(90)-y(270))^2+(z(90)-z(270))^2}=0,2236067977\;m \\
$$
Die Neigung der Ebene, in der die rechte Ellipse liegt, ist
$$
\epsilon=\arctan\left(\frac{y(0)-y(180)}{x(0)-x(180)}\right)= -0,7297276562=-41,8103148958°
$$
Der Umfang ist nur näherungsweise zu bestimmen.
Das sogenannte elliptische Integral lässt sich nur als Reihenentwicklung nummerisch berechnen.
Eine der besten Näherungen ist
$$
U_{Ellipse}\approx \pi (a+b)\left(1+\frac {3\lambda ^2}{10+\sqrt{ 4-3\lambda ^2 } }\right) \\
\text{mit } \quad \lambda ={\frac {a-b}{a+b}}
$$
Das ergibt für die Schweißnahtlänge einer Ellipse:
$$\sand{
Naht_{Ellipse}=U_{Ellipse} \approx 1,7738100707\;m
}\tag{3}
$$
Eine andere Methode zur Berechnung eines Kurvenstücks ist die Aufsummierung der Abstände von Punkten auf der Kurve.
Die Punkte auf der Ellipse können beliebig genau und in beliebiger Menge erzeugt werden.
Das Programm 3 zeigt den Vorgang.
function ellipse($n){
global $h;
global $rz;
global $yp;
$d=0;
for($i=0;$i<=360;$i=$i+360/$n){
$pz=$rz*sin($i/180*pi());
$py=$rz*cos($i/180*pi());
$kreis=($h/2-$py)/2;
$px=sqrt($kreis*$kreis-$pz*$pz);
if($py>$yp){$px=-$px;}
if($i==0){
$az=$pz; $ay=$py; $ax=$px;
}else{
$d=$d+sqrt(($ax-$px)**2+($ay-$py)**2+($az-$pz)**2);
$az=$pz; $ay=$py; $ax=$px;
}
}
return $d;
}
Programm 3
In der Tabelle 4 ist die Näherung mit diesem Programm für unterschiedliche Punktzahlen und dem relativen Fehler zum genauen Wert aus (3) angegeben.
| Anzahl Punkte | Umfangspolygon | Fehler |
|---|
| 10 | 1,7448054846 | -1,6351573717% |
| 100 | 1,7594623270 | -0,8088658404% |
| 1000 | 1,7724021836 | -0,0793707917% |
| 10000 | 1,7736695452 | -0,0079222391% |
| 100000 | 1,7737960208 | -0,0007920755% |
| 1000000 | 1,7738086658 | -0,0000792057% |
Tabelle 4
Die Summe aller Schweißnähte ist
$$\rand{
Naht_{gesamt}=Naht_{Kegelmantel}+Naht_{Zylindermantel}+2\cdot Naht_{Ellipse}=5,3892609279\;m
}$$