Zufallsexperimente

1.) Möglichkeiten

Die oben abgebildeten 3 Münzen können auf $2\cdot 2\cdot 2=2^3=8$ verschiedene Weisen fallen. Auch wenn nach dem Sortieren nur noch 4 Varianten übrig bleiben, müssen für die Wahrscheinlichkeitsberechnung alle berücksichtigt werden, denn die Gewichtung wäre sonst noch zu berücksichtigen und das würde die Arbeit nicht erleichtern.

Wenn man bei diesen 8 Möglichkeiten nach dem Sortieren die Positionen der Reihe nach dem Wert abfragt und die Häufigkeit zählt, erhält man eine zweidimensionale Liste von Treffern. Das sieht dann so aus:

Anzahl der Möglichkeiten = 8
		Wert
		1	2
Position	1	7	1
	2	4	4
	3	1	7

Tabelle 1

Mit den drei Würfeln in der obigen Abbildung kann man genauso vorgehen: es gibt $6\cdot 6\cdot 6=6^3=216$ Varianten die in der folgenden Liste wie bei den Münzen hergestellt wird:

Anzahl der Möglichkeiten = 216
		Wert
		1	2	3	4	5	6
Position	1	91	61	37	19	7	1
	2	16	40	52	52	40	16
	3	1	7	19	37	61	91

Tabelle 2

2.) Wahrscheinlichkeiten

Um von den Anzahlen in Tabelle 1 und Tabelle 2 zu den im Rätsel angegebenen Wahrscheinlichkeiten zu gelangen ist nur jede Zahl durch die Anzahl der Möglichkeiten zu teilen und mit 100% mal zunehmen.

Anzahl der Möglichkeiten = 8
		Wert
		1	2
Position	1	87,50000000%	12,50000000%
	2	50,00000000%	50,00000000%
	3	12,50000000%	87,50000000%

Tabelle 3

Anzahl der Möglichkeiten = 216
		Wert
		1	2	3	4	5	6
Position	1	42,12962963%	28,24074074%	17,12962963%	8,79629630%	3,24074074%	0,46296296%
	2	7,40740741%	18,51851852%	24,07407407%	24,07407407%	18,51851852%	7,40740741%
	3	0,46296296%	3,24074074%	8,79629630%	17,12962963%	28,24074074%	42,12962963%

Tabelle 4

In Tabelle 3 und Tabelle 4 sind die Wahrscheinlichkeiten der im Bild 1 gezeigten Münzen- und Würfel-Ergebnisse grün markiert.

3.) die Erzeugung der Tabellen 1 und 2

Mit den verhältnismäßig kleinen Zahlen kann man noch von Hand mit Papier und Stift die Zählungen durchführen. Aber ein kleines PHP-Programm erleichtert die Arbeit:


Function getlist($wert, $position) {            // Liste erzeugen
    for ($i = 1; $i <= $wert; $i++) {           // erzeugt und füllt Liste
        for ($j = 1; $j <= $position; $j++) {
            $liste[$i][$j] = 0;                 // Liste[wert][position]
        }
    }
    for ($j = 0; $j <= $position; $j++) {
        $w[$j] = 1;                             // Index j = 0 bis position setzt alles auf 1
        $a[$j] = 1;
    }                       
    do {                                        // Hauptschleife durchläuft alle Möglichkeiten
        $a = $w;                                // kopiert den aktuellen Zählerstand nach lokalen Speicher                                            
        sort($a);                               // sortiert lokalen Speicher
        for ($k = 1; $k <= $position; $k++) {
            $liste[$a[$k]][$k] ++;              // durchläuft alle Positionen und erhöht den Speicher bei dem zugehörigen Wert
        }
        $w[1] ++;                               // weiter zählen
        for ($l = 1; $l <= $position; $l++) {
            if ($w[$l] > $wert) {
                $w[$l] = 1;                     // rücksetzen
                if ($l < $position) {
                    $w[$l + 1] ++;              // Übertrag
                }
            } else {
                break;                          // kein weiterer Übertrag
            }
        }
    } while ($l <= $position);                  // Ende der Hauptschleife
    return $liste;                              // Ausgabe der Liste
}

Programm 1

Das Programm 1 liefert nur die Liste als 2-dimensionales Array, jedoch noch keine Ausgabe. Für die Ausgabe ist ein weiteres Programm zuständig:


function output($liste){                        // einfache HTML-Ausgabe einer Liste
    $wert = $liste[0][0];                       // lade Wert aus Liste
    $position = $liste[0][1];                   // lade Position aus Liste
    echo "<table style='text-align: right'>";   // Tabellenstart
    echo "<tr><th></th><th></th><th colspan='".$wert."'>Wert</th></tr>";
    echo "<tr>";                                // 2. Zeile: Kopf mit Wertezahlen
    echo "<th></th><th></th>";                  // Start mit 2 Leerfelder
    for ($h = 1; $h <= $wert; $h++) {
        echo "<th>".$h."</th>";                 // Wertezahlen
    }                              
    echo "</tr>";                               // Ende der 2.Zeile
    for ($v = 1; $v <= $position; $v++) {
        echo "<tr>";                            // Positionszeilen
        if ($v == 1) {
            echo "<th rowspan='$position'>"
            . "<div style='width: 20px; transform: rotate(-90deg)'>"
            . "Position</div></th>";
        }
        echo "<th>".$v."</th>";                 // 2. Spalte Positionsnummern
        for ($h = 1; $h <= $wert; $h++) {            
            echo "<td>".$liste[$h][$v]."</td>"; // weitere Spalten als Anzahl    
        }
        echo "</tr>";                           // Ende der Positionszeilen
    }
    echo "</table>";                            // Tabellenende                
}

Programm 2

Der Vorteil dieser Aufteilung ist, dass beliebige Herstellungsarten der Listen mit einem gemeinsamen Ausgabeprogramm zusammenspielen.

4.) zu den Rätselfragen 1a und 1b

Bei 50 Münzen gibt es $2^{50}= 1125899906842624$ Möglichkeiten. Das ist etwas zu viel für das Programm 1 denn die Laufzeit je nach Rechner kann über 40 Jahre dauern und die Zahlen würden den Integer-Bereich überschreiten. Gegen letzteres kann man mit der erweiterten Arithmetik (bc) noch etwas tun, aber diese verlangsamt die Abarbeitung zusätzlich. Man muss einen anderen Weg finden.

Für die Zahlen in der äußersten rechten Spalte der Liste gibt es eine Formel: $$liste_{n,m,k}=\sum\limits_{i=0}^{k-1}{n\choose k-i-1}\cdot (m-1)^{k-i-1} \\ \text{mit} \\ n = \text{Anzahl der Werte eines Generators (Münzen = 2, Würfel = 6)} \\ m = \text{Anzahl der Generatoren einer sortierten Reihe} \\ k = \text{Position in der Reihe beginnend bei eins bis m} \\ {n\choose k}= \frac{n!}{k! \cdot (n-k)!} = \text{Binomialkoeffizienten des Pascalschen Dreiecks} \\ $$ Auch für die äußerst linke Spalte kann diese Formel Verwendung finden, weil es dieselben Zahlen in umgekehrter Reihenfolge sind. Also wird der Wert von $k$ jeweils ersetzt durch $n+1-k$.

Da bei Münzen die Liste nur aus zwei Spalten besteht, ist damit eine vollständige Liste zu erzeugen. Die Tabelle 5 zeigt diese Liste.

Anzahl der Möglichkeiten = 1125899906842624
		Wert
		1	2
Position	1	1125899906842623	1
	2	1125899906842573	51
	3	1125899906841348	1276
	4	1125899906821748	20876
	5	1125899906591448	251176
	6	1125899904472688	2369936
	7	1125899888581988	18260636
	8	1125899788697588	118145036
	9	1125899251818938	655023686
	10	1125896746385238	3160457386
	11	1125886474107068	13432735556
	12	1125849120368268	50786474356
	13	1125727720717168	172186125456
	14	1125372860198568	527046644056
	15	1124435014542268	1464892300356
	16	1122184184967148	3715721875476
	17	1117260495271573	8639411571051
	18	1107413115880423	18486790962201
	19	1089359586996648	36540319845976
	20	1058953643613448	66946263229176
	21	1011824431369488	114075475473136
	22	944496985306688	181402921535936
	23	855747170042088	270152736800536
	24	747703916676488	378195990166136
	25	626155256640188	499744650202436
	26	499744650202436	626155256640188
	27	378195990166136	747703916676488
	28	270152736800536	855747170042088
	29	181402921535936	944496985306688
	30	114075475473136	1011824431369488
	31	66946263229176	1058953643613448
	32	36540319845976	1089359586996648
	33	18486790962201	1107413115880423
	34	8639411571051	1117260495271573
	35	3715721875476	1122184184967148
	36	1464892300356	1124435014542268
	37	527046644056	1125372860198568
	38	172186125456	1125727720717168
	39	50786474356	1125849120368268
	40	13432735556	1125886474107068
	41	3160457386	1125896746385238
	42	655023686	1125899251818938
	43	118145036	1125899788697588
	44	18260636	1125899888581988
	45	2369936	1125899904472688
	46	251176	1125899906591448
	47	20876	1125899906821748
	48	1276	1125899906841348
	49	51	1125899906842573
	50	1	1125899906842623

Tabelle 5

Die Liste der Wahrscheinlichkeiten zeigt u.a. die Lösungen der Rätselfragen 1a und 1b in Zeile 20 und 30 der Tabelle 6:

Anzahl der Möglichkeiten = 1125899906842624
		Wert
		1	2
Position	1	99,99999999999991%	0,00000000000009%
	2	99,99999999999547%	0,00000000000453%
	3	99,99999999988667%	0,00000000011333%
	4	99,99999999814584%	0,00000000185416%
	5	99,99999997769109%	0,00000002230891%
	6	99,99999978950740%	0,00000021049260%
	7	99,99999837812972%	0,00000162187028%
	8	99,99998950661286%	0,00001049338714%
	9	99,99994182220976%	0,00005817779023%
	10	99,99971929499534%	0,00028070500466%
	11	99,99880693341616%	0,00119306658384%
	12	99,99548925494643%	0,00451074505357%
	13	99,98470679991982%	0,01529320008018%
	14	99,95318885445741%	0,04681114554259%
	15	99,86989142716389%	0,13010857283611%
	16	99,66997760165945%	0,33002239834055%
	17	99,23266610836849%	0,76733389163151%
	18	98,35804312178658%	1,64195687821342%
	19	96,75456764638639%	3,24543235361361%
	20	94,05397737202819%	5,94602262797181%
	21	89,86806244677297%	10,13193755322703%
	22	83,88818398212265%	16,11181601787735%
	23	76,00561691508361%	23,99438308491639%
	24	66,40944831173172%	33,59055168826828%
	25	55,61375863296085%	44,38624136703915%
	26	44,38624136703915%	55,61375863296085%
	27	33,59055168826828%	66,40944831173172%
	28	23,99438308491639%	76,00561691508361%
	29	16,11181601787735%	83,88818398212265%
	30	10,13193755322703%	89,86806244677297%
	31	5,94602262797181%	94,05397737202819%
	32	3,24543235361361%	96,75456764638639%
	33	1,64195687821342%	98,35804312178658%
	34	0,76733389163151%	99,23266610836849%
	35	0,33002239834055%	99,66997760165945%
	36	0,13010857283611%	99,86989142716389%
	37	0,04681114554259%	99,95318885445741%
	38	0,01529320008018%	99,98470679991982%
	39	0,00451074505357%	99,99548925494643%
	40	0,00119306658384%	99,99880693341616%
	41	0,00028070500466%	99,99971929499534%
	42	0,00005817779023%	99,99994182220976%
	43	0,00001049338714%	99,99998950661286%
	44	0,00000162187028%	99,99999837812972%
	45	0,00000021049260%	99,99999978950740%
	46	0,00000002230891%	99,99999997769109%
	47	0,00000000185416%	99,99999999814584%
	48	0,00000000011333%	99,99999999988667%
	49	0,00000000000453%	99,99999999999547%
	50	0,00000000000009%	99,99999999999991%

Tabelle 6

5.) zu den Rätselfragen 2a, 2b, 3 und 4

Alle diese Fragen beschäftigen sich mit 12 Würfel. Deshalb ist nur eine Liste mit 6 Werten und 12 Positionen erforderlich, aus der die Antworten sofort abzulesen sind. Die Erzeugung dieser Liste in Tabelle 7 kann mit Programm 1 erfolgen und dauert bei einfachen Rechnern nur wenige Minuten (eine direkte Berechnung aller Feldinhalte wie bei den Münzen ist mir z.Z. nicht bekannt). Eine grafische Darstellung der Tabelle 7 zeigt das darunter befindliche Bild 2. Damit sind auch die Wahrscheinlichkeiten, wie in Tabelle 8 zu sehen ist, schnell berechnet.

Anzahl der Möglichkeiten = 2176782336
		Wert
		1	2	3	4	5	6
Position	1	1932641711	227363409	16245775	527345	4095	1
	2	1346704211	712637613	110531779	6806333	102339	61
	3	702172961	1080344799	352280737	40800095	1182033	1711
	4	272485461	1048658859	696737157	150508155	8363493	29211
	5	79126086	722973114	952718982	381131130	40494438	338586
	6	17251086	369612018	947053806	698223378	141828462	2813586
	7	2813586	141828462	698223378	947053806	369612018	17251086
	8	338586	40494438	381131130	952718982	722973114	79126086
	9	29211	8363493	150508155	696737157	1048658859	272485461
	10	1711	1182033	40800095	352280737	1080344799	702172961
	11	61	102339	6806333	110531779	712637613	1346704211
	12	1	4095	527345	16245775	227363409	1932641711

Tabelle 7

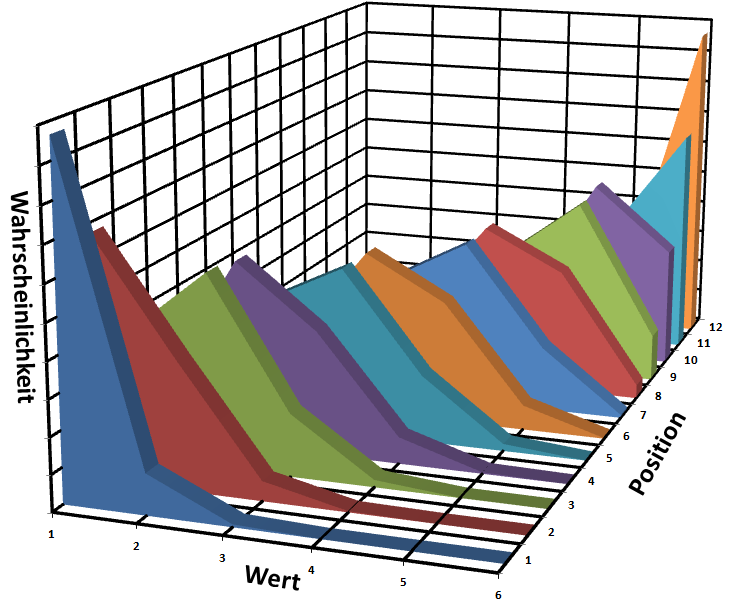
Bild 2

Anzahl der Möglichkeiten = 2176782336
		Wert
		1	2	3	4	5	6
Position	1	88,78433452%	10,44493082%	0,74632060%	0,02422589%	0,00018812%	0,00000005%
	2	61,86673737%	32,73811999%	5,07775983%	0,31267862%	0,00470139%	0,00000280%
	3	32,25738051%	49,63035491%	16,18355364%	1,87433049%	0,05430185%	0,00007860%
	4	12,51780927%	48,17472292%	32,00766312%	6,91424919%	0,38421356%	0,00134193%
	5	3,63500221%	33,21292635%	43,76730582%	17,50892240%	1,86028880%	0,01555443%
	6	0,79250395%	16,97974170%	43,50705123%	32,07593917%	6,51550960%	0,12925436%
	7	0,12925436%	6,51550960%	32,07593917%	43,50705123%	16,97974170%	0,79250395%
	8	0,01555443%	1,86028880%	17,50892240%	43,76730582%	33,21292635%	3,63500221%
	9	0,00134193%	0,38421356%	6,91424919%	32,00766312%	48,17472292%	12,51780927%
	10	0,00007860%	0,05430185%	1,87433049%	16,18355364%	49,63035491%	32,25738051%
	11	0,00000280%	0,00470139%	0,31267862%	5,07775983%	32,73811999%	61,86673737%
	12	0,00000005%	0,00018812%	0,02422589%	0,74632060%	10,44493082%	88,78433452%

Tabelle 8

Die grün hinterlegten Felder sind die Antworten auf die restlichen Rätselfragen.

Für Frage 2a sucht man in der 3. Zeile die Spalte mit dem Wert 3 auf.

Genauso ist für Frage 2b in der 5. Zeile die Spalte mit dem Wert 5 auszuwählen.

Für Frage 3 muss ein Blick auf die größte Wahrscheinlichkeit in Zeile 7 den Wert 4 finden.

Für Frage 4 ist die Spalte mit Wert 4 auf einen Maximalwert zu prüfen und man findet die Position 8.

6.) Zusammenfassung aller Lösungen der Rätselfragen

Frage	Wurf	Wert	Position	Wahrscheinlichkeit
1a	50 Münzen	1	20	94,05397737202819%
1b	50 Münzen	2	30	89,86806244677297%
2a	12 Würfel	3	3	16,18355364125851%
2b	12 Würfel	5	5	1,86028880013844%
3	12 Würfel	4	7	43,50705122590631%
4	12 Würfel	4	8	43,76730581849043%


Kurzbewertung dieser Information:
sehr gut	gut	befriedigend
ausreichend	mangelhaft	ungenügend

Lösungsbeschreibung des Preisrätsels vom August 2020