1.) Einleitung
Bei der Rätselfrage 3.) wird eine Beschäftigung mit der Gamma-Funktion nötig sein und auch bei der Rätselfrage 1.) kann das nicht schaden.
Dabei handelt es sich um eine Erweiterung der Fakultäts-Funktion auf nicht ganzzahlige Argumente.
Es ist zunächst nicht leicht einzusehen, was das bedeutet, wenn man gewohnt ist die Fakultät als Produkt
$$\sand{
n!=1\cdot2\cdot3\cdot4\cdot5\cdot\;...\;\cdot(n-2)\cdot(n-1)\cdot n=\prod_{k=1}^n k
}\tag{1}$$
zu sehen, welches immer beim Faktor 1 startet und bis zum Faktor n läuft.
Genau dieses Problem überwindet eine Überlegung, die auf einer anderen Definition beruht:
$$\sand{\begin{align}
n!&=n\cdot (n-1)! \\
1!&=1
\end{align}}\tag{2}$$
Nur so ist auch zu verstehen, was 0 ! bedeutet, indem für n = 1 eingesetzt wird:
$$\sand{\begin{align}
n!&=n\cdot (n-1)! \\
1!&=1\cdot 0! \\
1&=1\cdot 0! \\
1&=0!
\end{align}}\tag{3}$$
Für negative Zahlen ist die Fakultäts-Funktion nicht definiert.
Das kann man leicht verstehen, wenn man das gleiche Vorgehen wie (3) mit n = 0 versucht.
Insgesamt hat man sich mit dieser Definition von der obigen Produktform gelöst,
wenn auch noch nicht klar ist, wie man nicht ganzzahlige Werte berechnen kann.
Da kommt nun die Gamma-Funktion ins Spiel:
$$\sand{\begin{align}
\Gamma(x+1)&=x\cdot \Gamma(x) \\
\Gamma(1)&=1
\end{align}}\tag{4}$$
Der Unterschied zur Fakultäts-Funktion ist zunächst nur das um 1 größere Argument und der Übergang von n zu x,
welcher bedeutet, dass nun die Erweiterung auf alle reellen Zahlen mit Ausnahme der ganzen Zahlen kleiner als 1 vollzogen ist.
Für ganzzahlige n gilt dann
$$\sand{
\Gamma(n+1)=n!
}\tag{5}$$
Der Durchbruch zu nicht ganzzahligen Argumenten ist die folgende Gleichung:
$$\sand{
\Gamma(x)=\intop_0^\infty t^{x-1}e^{-t}dt
}\tag{6}$$
Das Integral ist für die schnelle Berechnung von beliebigen Werten der Gamma-Funktion nur schlecht geeignet (nummerische Integration),
aber für Mathematiker (oder den interessierten Leser) lässt sich damit beweisen, das es die obigen Definition (4) erfüllt.
Eine etwas bessere Gleichung zur Werte-Berechnung und eine weitere Verallgemeinerung auf alle komplexen Zahlen z ist
$$\sand{
\Gamma(z)=\sum_{n=0}^\infty \frac{(-1)^n}{n!(n+z)}+\intop_1^\infty t^{z-1}e^{-t}dt
}\tag{7}$$
2.) eine "gute" Näherung: die Stirling-Formel
Eine weitaus praktischere Berechnungsgrundlage ist die sogenannte Stirling-Formel.
Sie liegt in einer Form für Fakultäten und Gamma-Funktion vor:
$$\sand{\begin{align}
n!&\approx n^n\cdot\sqrt{2\pi n}\cdot e^S \\
\Gamma(n)&\approx n^n\cdot\sqrt{2\pi/n}\cdot e^S \\
\end{align}}\tag{8}$$
wobei für S oft nur das erste Glied einer Summe mit -n angegeben wird.
Für höhere Genauigkeiten kann S nach folgender Reihe entwickelt werden:
$$\sand{
S=-n+\sum\limits_{k=1}^m\frac{B_{2k}}{(2k-1)\cdot2k\cdot n^{2k-1}}=-n+\frac1{12n}-\frac1{360n^3}+\frac1{1260n^5}-\dots
}\tag{9}$$
wobei B
2k die rationalen
Bernoulli-Zahlen sind.
Die Anzahl der verwendeten Reihenglieder m darf nicht zu hoch gewählt werden denn die Reihe konvergiert nicht,
da die Bernoulli-Zahlen auf die Dauer schneller wachsen als die Potenzen von n.
Es gibt je nach Größe von n einen optimalen m-Wert.
Darüber hinaus verschlechtert sich die Näherung.
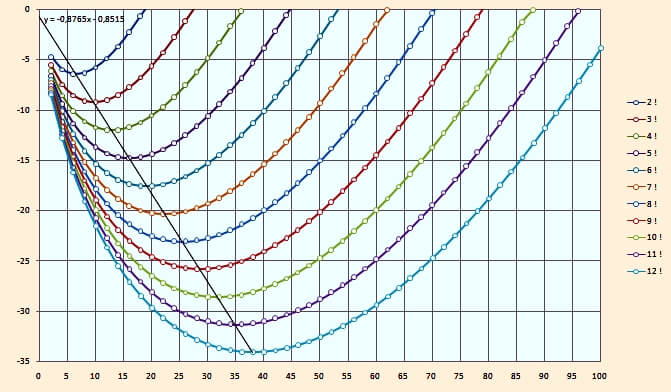
Für kleine n sieht das so aus:
Die Horizontal-Achse gibt die Zahl der verwendeten Summenglieder mit Bernoulli-Zahlen an,
die Vertikal-Achse den 10er-Logarithmus der erreichten Genauigkeit, anders ausgedrückt,
die Anzahl der übereinstimmenden Stellen mit dem genauen Funktionswert, wenn man die Zahlen der vertikalen Achse mit positivem Vorzeichen betrachtet.
Das Maximum der erreichbaren Genauigkeit liegt auf der schwarzen Gerade.
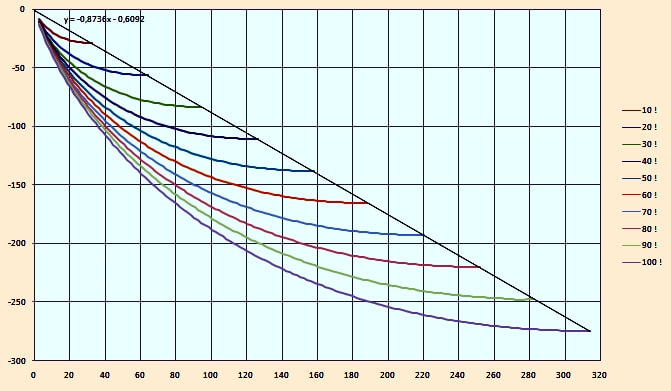
Auch für größere Werte von n kann man solch ein Diagramm zeichnen, es sind nur die Kurvenabschnitte nach dem Maximum der Genauigkeit weggelassen.
Es gibt also eine feste, wenn auch hier nur empirische Beziehungen zwischen der Zahl n,
der erreichbaren Genauigkeit g und der dafür erforderlichen Anzahl an Reihengliedern m.
$$\sand{
m=3,13\cdot n+0,8 \\
g=-2,735\cdot n -1,3
}$$
Mit diesen Beziehungen kann die folgende Tabelle mit willkürlich gewählten Werten für n berechnet werden:
| n | m | g |
|---|
| 1 | 4 | -4 |
| 3 | 10 | -10 |
| 10 | 32 | -29 |
| 30 | 95 | -83 |
| 100 | 314 | -275 |
| 300 | 940 | -822 |
| 1000 | 3.131 | -2.736 |
| 3000 | 9.391 | -8.206 |
| 10000 | 31.301 | -27.351 |
| 30000 | 93.901 | -82.051 |
| 100000 | 313.001 | -273.501 |
Hier sieht man deutlich, dass für kleine n keine hohen Genauigkeiten erreichbar sind.
Das wird bedeutsam im letzten Teil des Rätsels, wenn mit der Gamma-Funktion und kleinen Werten gerechnet werden muss.
Hingegen ist für die gesuchte Zahl 100000 ! eine völlig ausreichende Genauigkeit gegeben, wenn auch nicht für alle Stellen dieser Zahl.
Typischerweise wird das maximale m nie wirklich benutzt, aber es sollte klar sein,
dass die Stirling-Formel in Abhängigkeit von n natürliche Genauigkeitsgrenzen hat.
In folgender Tabelle ist die Ausgabe von Fakultäten einiger großer Zahlen in wissenschaftlicher Schreibweise mit 40 Nachkommastellen gelistet.
Die rot gerahmte Zahl ist die Lösung der Rätselfrage 1.)
Auch ist in der Spalte m die Anzahl der für diese Genauigkeit notwendigen Summenglieder ausgegeben.
Diese Zahlen sind geradzahlig, weil bei der Berechnung immer zwei Summanden zusammengefasst wurden.
| n | n! | m |
|---|
|
100 |
$9,3326215443944152681699238856266700490716\cdot 10^{157}$ |
14 |
|
1000 |
$4,0238726007709377354370243392300398571937\cdot 10^{2567}$ |
8 |
|
10000 |
$2,8462596809170545189064132121198688901481\cdot 10^{35659}$ |
6 |
|
100000 |
$2,8242294079603478742934215780245355184775\cdot 10^{456573}$ |
6 |
|
1000000 |
$8,2639316883312400623766461031726662911353\cdot 10^{5565708}$ |
4 |
|
10000000 |
$1,2024234005159034561401534879443075697677\cdot 10^{65657059}$ |
4 |
|
100000000 |
$1,6172037949214623863387731856128040432924\cdot 10^{756570556}$ |
4 |
|
1000000000 |
$9,9046265792229937372808211050657043217161\cdot 10^{8565705522}$ |
4 |
|
10000000000 |
$2,3257962056730833651049447199498788053954\cdot 10^{95657055186}$ |
2 |
|
100000000000 |
$3,7489285991050269624834755786222862334765\cdot 10^{1056570551815}$ |
2 |
|
1000000000000 |
$1,4036611603737560907201338677134505637738\cdot 10^{11565705518103}$ |
2 |
|
10000000000000 |
$2,4033300843401153446193633047672328213748\cdot 10^{125657055180974}$ |
2 |
Da es praktisch keine Fließkomma-Arithmetik für derart große Zahlen gibt, ist die Berechnung über die logarithmierte Stirling-Formel ausgeführt worden.
$$\sand{\begin{align}
n!&\approx n^n\cdot\sqrt{2\pi n}\cdot e^S \\
\ln(n!)&\approx n\cdot \ln(n)+\frac12\cdot\ln(2\pi n)+S
\end{align}}\tag{10}$$
Dabei bleiben die Zahlen übersichtlich im vorgegebenen Festkomma-Bereich und man muss das Ergebnis nur noch zerlegen in Mantisse und Exponent.
Am Beispiel von 100000 ! soll das hier gezeigt werden:
$$\sand{\begin{align}
\ln(100000!)&= 1051299,22189912186512927810820611085524934452314812389284 \\
\lg(100000!)&=\ln(100000!)/\ln(10) \\
\lg(100000!)&= 456573,45089997090836066339409474613233390244860227926559 \\
Exponent&=\lfloor(\lg(100000!)\rfloor=456573 \\
Mantisse&=\exp((\lg(100000!)-Exponent)\cdot\ln(10))\\
Mantisse&=2,82422940796034787429342157802453551847749491123279 \\
\end{align}}\tag{11}$$
Darin bedeutet:
- ln() der natürliche Logarithmus (zur Basis e)
- lg() der Briggssche Logarithmus (zur Basis 10)
- ⌊ ⌋ die Abrundung auf die nächste ganze Zahl (int- oder floor-Funktion)
- exp() die natürliche Exponentialfunktion ex
Eine Berechnung mit 1000 Stellen und die tatsächliche genaue Zahl,
die durch Multiplikationen berechnet wurde, kann man
hier nachlesen.
3.) die zweite Rätselfrage: Anzahl der Nullen
Um die Frage nach der Anzahl der Nullen am Ende des Produktes der Zahlen von 1 bis 100000 zu beantworten,
benötigen wir die Anzahl der Faktoren von 10, die im Produkt enthalten sind.
Das führt zu der Frage nach der Anzahl der enthaltenen Primfaktoren 2 und 5,
weil jeweils ein Faktor 2 und ein Faktor 5 zusammen eine Null am Ende erzeugen.
Wie oft also ist die 2 als Faktor enthalten?
Wir kennen alle Faktoren des Produkts, nämlich die Zahlen von 1 bis 100000.
Dabei ist jede zweite Zahl gerade, enthält also den Faktor 2.
das ergibt schon mal 100000 : 2 = 50000 gerade Zahlen.
Von diesen ist wiederum jede zweite ein weiteres mal durch 2 teilbar,
nämlich 4, 8, 12, 16 ... , die also mindestens 2 mal den Faktor 2 enthalten.
Wenn beim Teilen einer ungeraden Zahl ein Rest bleibt, so kann man den weglassen, also auf die ganze Zahl abrunden.
Diese Überlegungen fortgesetzt ergibt folgende Rechnung:
Anzahl des Primfaktors 2 in 100000 ! :
50000+25000+12500+6250+3125+1562+781+390+195+97+48+24+12+6+3+1=99994
Das gleiche kann man auch für alle anderen Primfaktoren machen, wobei hier besonders die 5 gefragt ist:
Anzahl des Primfaktors 5 in 100000 ! :
20000+4000+800+160+32+6+1=24999
Es sind also weniger Faktoren 5 als Faktoren 2 enthalten.
Für die Anzahl der Nullen gilt die kleinere Zahl:
$$\rand{\min(99994,24999)=24999}$$
Man kann so die gesamte Primfaktorzerlegung einer Fakultät angeben ohne diese Zahl genau zu kennen:
100000 ! = 299994⋅349995⋅524999⋅716662⋅119997⋅138331⋅176249⋅195554⋅234544 ...
4.) die Gammafunktion für kleine nicht ganzzahlige Argumente
Die Gamma-Funktion unterscheidet sich von der Fakultät durch einen kontinuierlichen Verlauf zwischen den ganzzahligen Werten der Fakultät.
Es ist zusätzlich zu beachten, dass es einen Versatz um 1 im Argument der beiden Funktionen gibt:
$$\sand{
x!=\Gamma(x+1)
}$$
Die nicht ganzzahligen Werte von x sind in der Fakultät nicht definiert.
Trotzdem wird manchmal (Windows- und Google-Rechner) so getan, als ob auch das erlaubt sei und es wird z.B. folgendes berechnet:
| Windows-Rechner: | $\pi !=7,1880827289760327020821943451248$ |
| Google-Rechner: | $\pi !=7.18808272898$ |
Richtig wäre es aber, mit der Gamma-Funktion zu arbeiten und das sieht dann so aus:
Dieser Gamma-Rechner kann hier mit anderen Zahlen oder Ausdrücken benutzt werden.
Arithmetik, Klammern und Funktionen wie exp(), ln(), sin(), cos(), pi(), sqrt() und Potenzieren mit ganzen positiven Zahlen durch ^ ist vorhanden.
Dezimalzahlen mit Punkt oder Komma sind erlaubt, jedoch keine Fließkomma-Darstellung, die aber leicht nachgebaut werden kann, z.B 2,27/10^18 für 2,27e-18.
Darüber hinaus ist der Gamma-Rechner auch außerhalb dieser Seite direkt aufrufbar, auch mit Parameterübergabe, z.B. so:
https://wissenschaftsreisen.de/quiz-antwort/gamma.php?gamma=1&n=pi()
Wer mit geringerer Genauigkeit zufrieden ist kann auch mit EXCEL die Gamma-Funktion berechnen.
Ab EXCEL 2010 ist diese Funktion enthalten.
Für ältere Versionen kann man folgende VBA-Funktion erstellen:
Function gamma(n, Optional ausgabe = 0)
If n < 50 Then off = 50 - Int(n) Else off = 0
vorzeichen = 1
Pi = 4 * Atn(1)
m = 10
n = n - 1 + off
Dim bernoulli(10)
bernoulli(0) = 1 / 6
bernoulli(1) = -1 / 30
bernoulli(2) = 1 / 42
bernoulli(3) = -1 / 30
bernoulli(4) = 5 / 66
bernoulli(5) = -691 / 2730
bernoulli(6) = 7 / 6
bernoulli(7) = -3617 / 510
bernoulli(8) = 43867 / 798
bernoulli(9) = -174611 / 330
summe = (Log(n) - 1) * n + Log(2 * Pi * n) / 2
For i = 1 To m
sum0 = bernoulli(i - 1) / (2 * i * (2 * i - 1) * n ^ (2 * i - 1))
i = i + 1
sum1 = bernoulli(i - 1) / (2 * i * (2 * i - 1) * n ^ (2 * i - 1))
sum2 = sum0 + sum1
If sum2 <= 0 Then Exit For
summe = summe + sum2
Next i
For i = 0 To off - 1
If n - i < 0 Then
summe = summe - Log(i - n)
vorzeichen = -vorzeichen
Else
summe = summe - Log(n - i)
End If
Next i
If ausgabe = 3 Then gamma = vorzeichen
If ausgabe = 2 Then gamma = summe
If ausgabe = 1 Then
pot = summe / Log(10)
exponent = Int(pot)
mantisse = Exp((pot - exponent) * Log(10))
If exponent >= 0 Then vtext = "+" Else vtext = ""
gamma = vorzeichen * mantisse & vtext & exponent
End If
If ausgabe = 0 Then gamma = Exp(summe) * vorzeichen
End Function
Die Berechnung läuft hier genau wie im obigen Gamma-Rechner über die logarithmische Stirling-Formel (Zeile 20).
Die Summenglieder mit Bernoulli-Zahlen (Zeile 8-18) werden paarweise zusammengefasst
und solange weiter zum Anfangsterm hinzugefügt, bis die vorgegebene Genauigkeit erreicht ist (Zeile 22-29).
Falls die Gamma-Funktion mit Argumenten kleiner als 50 (im obigen Gamma-Rechner 100) zu berechnen ist,
wird ein ganzzahliger Offset hinzu addiert, um eine ausreichend hohe Genauigkeit bei größeren Werten zu erhalten.
Das muss natürlich dann wieder korrigiert werden, indem durch die im Offset "zu viel" angegebenen Faktoren dividiert wird (Zeile 31-38).
Folgendes Beispiel mit Offset=3 zeigt das Prinzip:
$$\sand{
\Gamma(x)=\frac{\Gamma(x+3)}{(x+2)\cdot(x+1)\cdot x}
}\quad\text{oder}\quad\sand{
x!=\frac{(x+3)!}{(x+3)\cdot(x+2)\cdot (x+1)}
}$$
Das Dividieren läuft auf der Ebene der Logarithmen natürlich durch Subtrahieren ab.
Wenn ein Faktor negativ ist, wird das Vorzeichen abgetrennt und separat verrechnet.
Die Ergebnis-Ausgabe (Zeile 40-49) kann in unterschiedlicher Weise erfolgen:
Ohne Eingabe eines zweiten Parameters wird der Wert der Gamma-Funktion im normalen EXCEL-Zahlenbereich ausgegeben.
| selbst definierte Gamma-Funktion in EXCEL |
|---|
| 2. Parameter | Ausgabe |
|---|
| 0 oder leer | Wert der Gamma-Funktion
mit normalem EXCEL-Zahlenbereich |
| 1 | Wert der Gamma-Funktion
mit erweitertem Zahlenbereich als Text |
| 2 | Logarithmus des Betrags der Gamma-Funktion |
| 3 | Vorzeichen der Gamma-Funktion |
5.) die dritte Rätselfrage
Gesucht ist die Lösung für x in der Gleichung
$$\sand{
\Gamma(x)=x
}$$
Das bedeutet: es sind die Schnittpunkte der beiden folgenden Funktionen gesucht:
$$\sand{
\begin{align}
y &=f(x)=\Gamma(x) \\
y &=f(x)=x
\end{align}
}$$
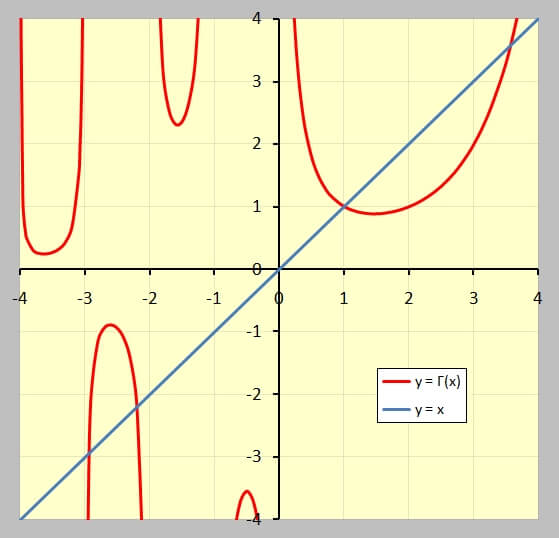
Die erste Funktion ist die Gamma-Funktion (rot), die zweite (blau) die Gerade durch den Nullpunkt mit der Steigung 1.
Die Schnittpunkte der blauen Geraden mit der roten Kurve zeigen die Position der reellen Lösungen der obigen Gleichung.
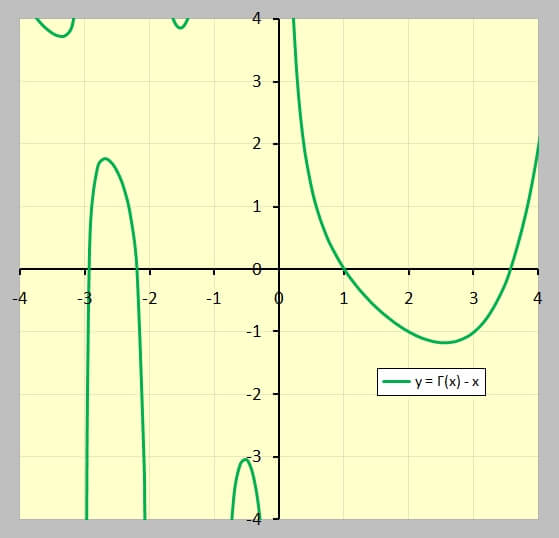
Zur Lösung betrachtet man die Funktion
$$\sand{
f(x)=\Gamma(x)-x
}$$
und deren Nullstellen.
Sie lassen sich aus dem folgenden Diagramm ungefähr ablesen.
$$\sand{
\begin{align}
x_1 &\approx 3,55 \\
x_2 &=1 \\
x_3 &\approx -2,2 \\
x_4 &\approx -2.94
\end{align}
}$$
Zur genaueren Bestimmung der 4 Nullstellen kann man sich mit dem Newton-Verfahren schrittweise nähern:
$$\sand{
x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}
}$$
Dazu sind als Startwerte die ungefähren Nullstellen und die Steigung an dieser Stelle abzuschätzen.
Umso genauer die Anfangswerte bekannt sind umso schneller konvergiert das Ergebnis.
Die folgenden 4 Tabellen zeigen den Ablauf der Näherung.
| $n$ | $x_{1_n}$ |
|---|
| 0 | 3,5500000000000000000000000000000000000000 |
| 1 | 3,5622389192017188426476549029028577821336 |
| 2 | 3,5623822660525007851521976402971837529388 |
| 3 | 3,5623822853908973395317427711385643918768 |
| 4 | 3,5623822853908976914156443427474938033750 |
| 5 | 3,5623822853908976914156443427476103117811 |
| $f'(x_1)$ | 3,0025408862604845141911283054345300338209 |
|---|
| $n$ | $x_{2_n}$ |
|---|
| 0 | 1,0100000000000000000000000000000000000000 |
| 1 | 1,0000621397838623955514380903129329743427 |