1.) Einleitung
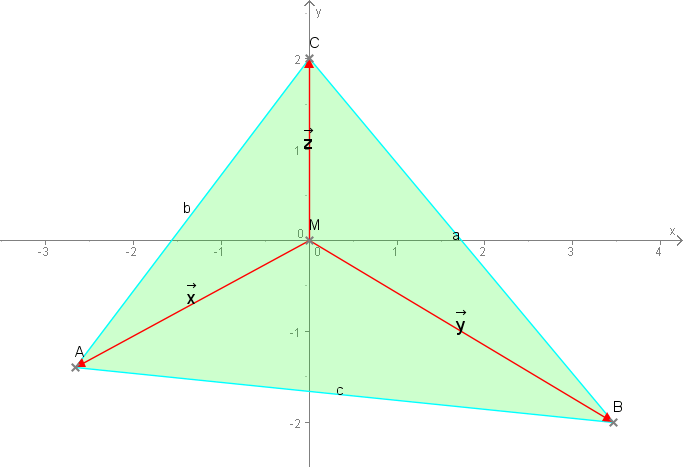
Obwohl ein nicht fixiertes Dreieck als Ausgangspunkt für dieses Rätsel angenommen wurde, ist es für die Berechnungen der Vektorlängen aus den Seitenlängen einfacher, wenn man das Dreieck wie in der Zeichnung weiter unten so auf Koordinaten platziert dass der Ursprung im Punkt A liegt. Man dreht das Koordinatensystem dann so, dass B auf die x-Achse zu liegen kommt. Dadurch erreicht man Vereinfachungen in den Formeln, weil einige Parameter zu Null werden. Notwendig ist diese Vorgehensweise nicht.
2.) Berechnung der Dreieckseiten aus der Länge der Sternvektoren
Zunächst einmal ist es sehr einfach, aus gegebenen "Sternvektoren" $\vec x$, $\vec y$ und $\vec z$ die Länge der Dreieckseiten $a$, $b$ und $c$ zu bestimmen. Dazu betrachtet man in der oberen Zeichnung die Dreiecke $\triangle BCM$, $\triangle CAM$ und $\triangle ABM$ und wendet den Cosinussatz an, z.B. auf das Dreieck $\triangle BCM$ $$\sand{a^2=y^2+z^2-2yz\cdot\cos\mu}$$ und weil der Winkel bei $M$ zwischen $\vec y$ und $\vec z$ und auch die anderen Winkel immer $\mu=120°$ sind, wird $\cos\mu=-\frac12$ für alle obigen Dreiecke. Daraus folgt: $$\sand{\begin{array}{ccc} a=+\sqrt{y^2+z^2+yz} \\ b=+\sqrt{x^2+z^2+xz} \\ c=+\sqrt{x^2+y^2+xy} \\ \end{array}}$$3.) Berechnung der Länge der Sternvektoren aus den Dreieckseiten
Das Umgekehrte ist wesentlich schwieriger. Man kann das obige Gleichungssystem nicht mit einfachen Mitteln nach $x$, $y$ und $z$ auflösen. Andererseits scheint es aber klar, dass sich für jedes Dreieck eine Möglichkeit findet, einen Stern mit passenden, gegebenenfalls auch negativen Vektorlängen zuzuordnen.Das Problem ist unter anderem Namen bekannt und hatte auch eine andere Zielsetzung. Der französische Mathematiker Pierre de Fermat (1607–1665) stellte dem italienischen Mathematiker Evangelista Torricelli (1608–1647) die folgende Aufgabe: Gegeben wird ein Dreieck. Bestimme einen Punkt P, so dass die Summe seiner Abstände zu den Eckpunkten des Dreiecks minimal ist. Im Laufe der Zeit ist dieser Punkt als Punkt von Fermat in die Mathematik eingegangen. Er ist identisch mit dem Punkt $M$ in obiger Zeichnung und wird ab hier umbenannt zum Punkt $F$. Die für dieses Rätsel bedeutende Eigenschaft des Punktes $F$ von Fermat ist, dass die Winkel immer 120° betragen. Deshalb ist es sinnvoll, den Beweis durchzugehen, der in dieser Form besonders anschaulich von Joseph Ehrenfried Hofmann (1900-1973) im Jahre 1929 gelang:
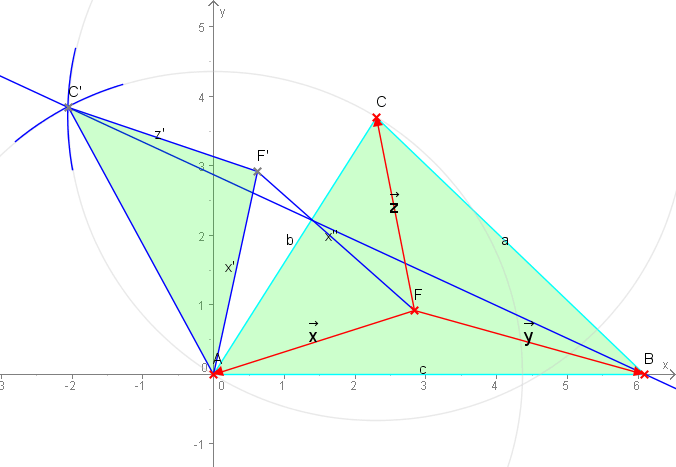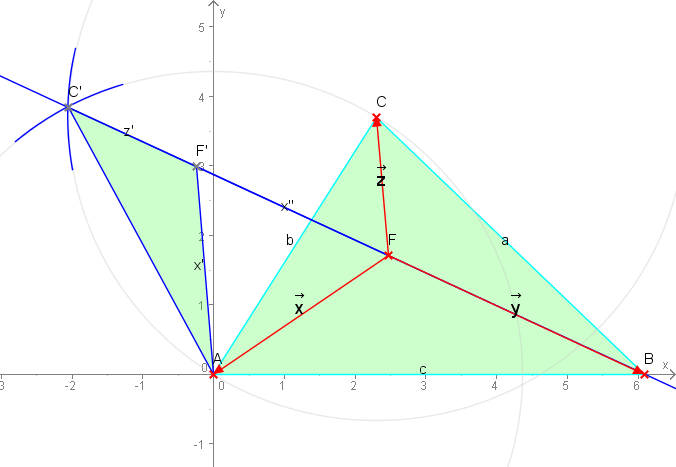
Auf der bewegten Grafik ist neben dem schon von oben bekannten Dreieck zusätzlich folgendes zu sehen: Ein Punkt $C'$ links oben, der durch die angedeuteten Kreisbögen konstruiert wurde und gegenüber dem Punkt $C$ um den Koordinatenursprung um 60° nach links gedreht wurde. Er bildet mit den Punkte $A$ und $C$ zusammen ein gleichseitiges Dreieck. Weiterhin gibt es einen Punkt $F$ in zwei Positionen, zunächst in einer willkürlichen tiefen Position und zusätzlich in der richtigen auf der Verbindungslinie von Punkt $C'$ nach Punkt $B$. Auch ist ein Punkt $F'$ konstruiert worden, der mit dem Punkt $F$ und dem Punkt $A$ ein gleichseitiges Dreieck bildet. Punkt $F'$ ist also genau wie Punkt $C'$ um 60° nach links um den Ursprung (Punkt $A$) gedreht.
Deshalb sind auch die Dreiecke $\triangle AFC$ und $\triangle AF'C'$ in beiden Bildvarianten jeweils von den Seitenabmessungen gleich. Das ist insbesondere interessant für die Strecken $x$, $x'$ und $x''$ einerseits und $z$ und $z'$ andererseits. Verfolgt man in beiden Bildvarianten den Weg von Punkt $C'$ nach Punkt $B$ so ist das die Summe aus den Beträgen der Vektoren $\vec x$, $\vec y$ und $\vec z$. Aber nur in der richtigen Variante ist das der kürzeste Weg und damit ist das Minimalproblem von Fermat gelöst.
Für dieses Rätsel ist die Eigenschaft von Bedeutung, dass aus Sicht des Punktes $F$ die drei Eckpunkte des Dreiecks jeweils unter dem gleichen Winkel von 120° gesehen werden. Ein Beweis dafür ist schnell erbracht: $$\sand{\angle AFB=\angle F'FB-\angle F'FA=180°-60°=120°}$$ Es ist mit Hilfe der obigen Erkenntnis nun möglich, aus den gegebenen Dreieckseiten die Koordinaten des Fermatpunktes zu berechnen. Damit sind dann auch die letztlich gesuchten Vektorlängen zu bestimmen. $$\sand{\begin{array}{ccc} \left|\vec x\right|=+\sqrt{(x_A-x_F)^2+(y_A-y_F)^2} \\ \left|\vec y\right|=+\sqrt{(x_B-x_F)^2+(y_B-y_F)^2} \\ \left|\vec z\right|=+\sqrt{(x_C-x_F)^2+(y_C-y_F)^2} \\ \end{array}}$$ Dabei ist gemäß obiger Zeichnung bekannt: $\tond{x_A=y_A=0}\quad \tond{x_B=c}\quad \tond{y_B=0}\quad \tond{x_C=b\cdot\cos\alpha}\quad \tond{y_C=b\cdot\sin\alpha}$. Auch $\tond{\cos\alpha=\frac{a^2-b^2-c^2}{-2bc}}$ ist aus dem Cosinussatz bekannt und demzufolge auch $\tond{\sin\alpha=\sqrt{1-\cos^2\alpha}}$. Unbekannt ist nur $\tona{x_F}$ und $\tona{y_F}$.
Das was oben beschrieben zur Konstruktion der Geraden durch $C'$ und $B$ führte, kann man aus Symmetriegründen auch für einen zu konstruierenden Punkt $C''$ machen, der dann eine Gerade durch sich und durch $A$ festlegt. Da auch auf dieser Geraden der Fermatpunkt liegen muss ist zur Bestimmung der noch fehlenden Koordinaten der Schnittpunkt beider Geraden zu berechnen. $$\sand{\begin{array}{cc} \text{1. Geradengleichung:}\quad y=m_1x+n_1\quad\text{mit}\quad m_1=\frac{y_B-y_{C'}}{x_B-x_{C'}}\quad\text{und}\quad n_1=m_1\cdot x_B \\ \text{2. Geradengleichung:}\quad y=m_2x+n_2\quad\text{mit}\quad m_2=\frac{y_A-y_{C''}}{x_A-x_{C''}}\quad\text{und}\quad n_2=m_2\cdot x_A \\ \end{array}}$$ Die Koordinaten des Schnittpunktes sind dann: $$\sand{\begin{array}{cc} x_F=\frac{n_2-n_1}{m_1-m_2} \\ y_F=\frac{m_1 n_2-m_2 n_1}{m_1-m_2} \\ \end{array}}$$ Es stehen jetzt nur noch die Koordinaten von $C'$ und $C''$ aus, die in den Geradengleichungen benötigt werden, aber das ist verhältnismäßig einfach. Beide gehen aus den bekannten Koordinaten von $C$ hervor, $C'$ durch Linksdrehung um $A$ mit 60°, $C''$ durch Rechtsdrehung um $B$ mit ebenfalls 60°. Man wendet dabei die sogenannte Drehmatrix oder Rotationsmatrix an. Dabei ist zu beachten, dass die Drehung immer um den Ursprung erfolgt. Bei $C'$ ist das auch gewünscht, aber $C''$ muss um $B$ drehen. Deshalb ist zunächst eine Verschiebung des gewünschten Drehpunktes zum Ursprung erforderlich, nach der Drehung kann dann die Rückverschiebung erfolgen. Das schreibt sich dann so: $$\sand{\begin{array}{cc} \begin{pmatrix}x_{C^{'}} \\ y_{C^{'}} \end{pmatrix} = \begin{pmatrix}\cos 60^{\circ} & -\sin 60^{\circ} \\ \sin 60^{\circ} & \cos 60^{\circ} \end{pmatrix} \begin{pmatrix}x_C \\ y_C \end{pmatrix} \\ \begin{pmatrix}x_{C^{''}}-x_B \\ y_{C^{''}}\end{pmatrix} = \begin{pmatrix}\cos -60^{\circ} & -\sin -60^{\circ} \\ \sin -60^{\circ} & \cos -60^{\circ} \end{pmatrix} \begin{pmatrix}x_C-x_B \\ y_C \end{pmatrix} \\ \end{array}}$$ Hier kommt die Frage auf, wieso diese letzten Gleichungen den Anschein einer Unsymmetrie erwecken, denn bisher waren alle vorangegangen Gleichungen so aufgebaut, dass zyklische Vertauschungen von Punkt $A$, $B$ und $C$ ohne Einfluss auf das Ergebnis blieb. Warum ist also mal eine Rechtsdrehung und mal eine Linksdrehung vorhanden und warum muss mal eine Verschiebung und mal keine Verschiebung berücksichtigt werden? Es sind willkürliche Festlegungen daran schuld. Insbesondere ist die Lage von Punkt $A$ auf dem Koordinatenursprung eine Ursache, die zu Vereinfachungen lockt. Würden wir das Koordinatensystem beliebig verschieben, wäre $x_A$, $y_A$ und $y_B$ nicht mehr Null und die Gleichungen würden dann so lauten: $$\sand{\begin{array}{cc} \begin{pmatrix}x_{C^{'}}-x_A \\ y_{C^{'}}-y_A \end{pmatrix} = \begin{pmatrix}\cos 60^{\circ} & -\sin 60^{\circ} \\ \sin 60^{\circ} & \cos 60^{\circ} \end{pmatrix} \begin{pmatrix}x_C-x_A \\ y_C-y_A \end{pmatrix} \\ \begin{pmatrix}x_{C^{''}}-x_B \\ y_{C^{''}}-y_B\end{pmatrix} = \begin{pmatrix}\cos -60^{\circ} & -\sin -60^{\circ} \\ \sin -60^{\circ} & \cos -60^{\circ} \end{pmatrix} \begin{pmatrix}x_C-x_B \\ y_C-y_B \end{pmatrix} \\ \end{array}}$$ Diese Form ist sicherlich die allgemeinere, weil sie den Spezialfall "Punkt $A$ liegt auf dem Ursprung und Punkt $B$ auf der x-Achse" beinhaltet. Nun noch zur Drehung. Die Konstruktion von $C''$ könnte ebenso gut auch als Linksdrehung des Punktes $B$ um den Punkt $C$ angesehen werden und trüge dann aus Analogie zu $C'$ besser die Bezeichnung $B'$. Die Position wäre die gleiche wie von $C''$, aber die Gleichungen sähen dann so aus: $$\sand{\begin{array}{cc} \begin{pmatrix}x_{C^{'}}-x_A \\ y_{C^{'}}-y_A \end{pmatrix} = \begin{pmatrix}\cos 60^{\circ} & -\sin 60^{\circ} \\ \sin 60^{\circ} & \cos 60^{\circ} \end{pmatrix} \begin{pmatrix}x_C-x_A \\ y_C-y_A \end{pmatrix} \\ \begin{pmatrix}x_{B^{'}}-x_C \\ y_{B^{'}}-y_C \end{pmatrix} = \begin{pmatrix}\cos 60^{\circ} & -\sin 60^{\circ} \\ \sin 60^{\circ} & \cos 60^{\circ} \end{pmatrix} \begin{pmatrix}x_B-x_C \\ y_B-y_C \end{pmatrix} \\ \end{array}}$$ Damit ist die volle Symmetrie wieder hergestellt. Nur das Rechnen ist etwas erschwert, weil nicht so viele Werte gleich Null sind. Mit der Ersetzung $\sin 60°= \sqrt{3}/2$ und $\cos 60°=1/2$ lässt sich schreiben: $$\sand{\begin{array}{cc} \begin{pmatrix}x_{C^{'}}-x_A \\ y_{C^{'}}-y_A \end{pmatrix} =\frac12\cdot \begin{pmatrix}1 & -\sqrt{3} \\ \sqrt{3} & 1 \end{pmatrix} \begin{pmatrix}x_C-x_A \\ y_C-y_A \end{pmatrix} \\ \begin{pmatrix}x_{B^{'}}-x_C \\ y_{B^{'}}-y_C \end{pmatrix} =\frac12\cdot \begin{pmatrix}1 & -\sqrt{3} \\ \sqrt{3} & 1 \end{pmatrix} \begin{pmatrix}x_B-x_C \\ y_B-y_C \end{pmatrix} \\ \end{array}}$$ Ohne Matrix-Form schreiben sich die Gleichungen so: $$\sand{\begin{array}{cccc} x_{C^{'}}-x_A = \frac12\cdot( 1\cdot(x_C-x_A) -\sqrt{3}\cdot(y_C-y_A) ) \\ y_{C^{'}}-y_A = \frac12\cdot( \sqrt{3}\cdot(x_C-x_A) +1\cdot(y_C-y_A) ) \\ x_{B^{'}}-x_C = \frac12\cdot( 1\cdot(x_B-x_C) -\sqrt{3}\cdot(y_B-y_C) ) \\ y_{B^{'}}-y_C = \frac12\cdot( \sqrt{3}\cdot(x_B-x_C) +1\cdot(y_B-y_C) ) \\ \end{array}}$$ Es ist nun alles da. Wenn man mit Zahlen rechnen will ist das schrittweise Vorgehen sinnvoll. Da aber auch die Frage zu beantworten ist, ob es eine geschlossene Formel gibt ist die Antwort: ja, aber man muss sich darauf einstellen mit Monster-Ausdrücken loszulegen. Wie sich ja gezeigt hat sind alle Gleichungen symmetrisch aufgebaut. Wenn man also z.B. für $\vec x$ einen Ausdruck gefunden hat kann man durch zyklisches Austauschen auch die Ausdrücke für $\vec y$ und $\vec z$ finden. $$\sand{\left|\vec x\right|^2=(x_A-x_F)^2+(y_A-y_F)^2}\quad\text{mit}\quad x_A=y_A=0$$ $$\sand{\left|\vec x\right|^2=x_F^2+y_F^2}$$ $$\sand{=\left(\frac{n_2-n_1}{m_1-m_2}\right)^2+\left(\frac{m_1 n_2-m_2 n_1}{m_1-m_2}\right)^2}\quad\text{mit}\quad n_1=m_1\cdot c\quad\text{und}\quad n_2=0$$ $$\sand{=\left(\frac{m_1\cdot c}{m_1-m_2}\right)^2 + \left(\frac{m_2 m_1\cdot c}{m_1-m_2}\right)^2}$$ $$\sand{=\left(\frac {m_1\cdot c}{m_1-m_2}\right)^2\cdot(1+{m_2}^2)}$$ $$\sand{=\left(\frac {m_1\cdot c}{m_1-m_2}\right)^2\cdot(1+{m_2}^2)} \quad\text{mit}\quad m_1=\frac{y_{C'}-c}{x_{C'}} \quad\text{mit}\quad m_2=\frac{y_{C''}}{x_{C''}}$$ Bis hier sieht das alles noch übersichtlich aus, aber wenn man nun anfängt, die Ausdrücke für $m_1$ und $m_2$ einzusetzen, dann beginnt die Formel aus den Fugen zu platzen. Das möchte ich nun aber dem interessierten Leser überlassen.