Preisrätsel Oktober 2014
Dreieck einmal anders
Üblicherweise wird ein nicht an einem speziellen Ort fixiertes Dreieck durch drei Angaben festgelegt,
z.B. durch die Längen der drei Seiten oder durch zwei Seiten und dem eingeschlossenen Winkel.
Bei Angaben von einer Seite und zwei Winkel oder bei zwei Seiten und dem nicht eingeschlossenen Winkel
gibt es zum Teil sehr komplexe Einschränkungen und gegenseitige Abhängigkeiten der gültigen Wertebereiche von Seitenlängen und Winkel.
Selbst bei der Angabe von drei Seiten darf die Summe der beiden kleinsten Seiten
nicht kleiner als die Länge der größten Seite sein.
Wenn man zu Dreiecken mit fester Position und Ausrichtung übergeht, wird die Sache noch schwieriger. Es kommen drei weitere Angaben hinzu, die durch noch komplexere Bedingungen und Abhängigkeiten eingeschränkt werden. Nur wenige Kombinationen von Angaben zur Festlegung eines fixierten Dreiecks sind unproblematisch, so z.B. die Angaben der Koordinaten der drei Eckpunkte mit jeweils zwei Werten. Hier sind alle sechs Werte ohne Einschränkung und unabhängig voneinander wählbar.
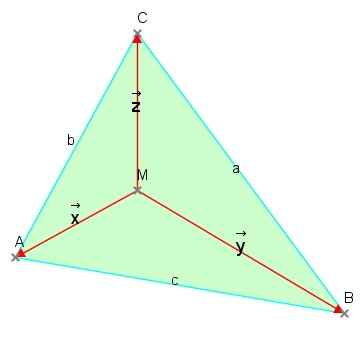
Will man solche Freiheiten auch für den Wertebereich der drei Angaben bei nicht fixierten Dreiecken erreichen, darf man nicht auf Seitenlängen und Winkel aufbauen, denn diese sind immer stark eingeschränkt. Seitenlängen dürfen z.B. nicht negativ sein. Da bietet sich als Ausweg ein System von drei Vektoren $\vec x$, $\vec y$ und $\vec z$ an, die mit gleichen Winkeln zueinander (120°) von einem Zentralpunkt M ausgehend mit ihren Endpunkten die Eckpunkte eines Dreiecks festlegen (siehe Zeichnung). Hier sind unter den oben angenommenen Bedingungen allein die Längen der drei Vektoren zur Bestimmung eines Dreiecks nötig. Dabei besteht völlige Freiheit in Bezug auf den Wertebereich dieser drei Längen. Auch negative Längen sind bei Vektoren zulässig (nicht zu verwechseln mit dem Betrag eines Vektors, der immer positiv ist).
Rätselaufgabe:
a) zur Einstimmung: Wie lang sind die Dreieckseiten a, b und c wenn die Längen der Vektoren $x=\frac37$, $y=\frac47$ und $z=\frac57$ sind?
b) schon schwieriger: Wie lang sind die Vektoren $\vec x$, $\vec y$ und $\vec z$ wenn die Längen der Dreieckseiten $a=\frac37$, $b=\frac47$ und $c=\frac57$ sind?
c) Gibt es für die Berechnung der Vektorenlängen aus den Seitenlängen des Dreiecks einfache algebraische Formeln und wie lauten sie?
Viel Spaß bei der Suche nach einer Lösung.