1.) statistische Annäherungen
Wenn man lange genug den Bewegungen in der obigen Animation folgt, die Zahlen in den Kreisen notiert und am Ende diese Anzahlen in Prozentwerte umrechnet, hat man das Rätsel gelöst. Der Haken an dieser Lösung ist: um eine ausreichend genaue Datenbasis zu erhalten dauert sie länger als das Universum alt ist.Man kann den Ablauf natürlich deutlich beschleunigen, wenn man die Wartezeiten des Aufschreibens verkürzt und eine automatisch Zählung programmiert. Das wird auch im Folgenden mit einem kleinen Programm gemacht und es laufen für jeden Radius fünf Durchgänge mit je 100.000 Zufallspositionen ab. Dies findet aktuell beim Aufruf dieser Seite statt und dauert weniger als eine Sekunde und erzeugt bei jedem Neustart der Seite zufällige etwas andere Werte.
function abdeckung($n, $r) {
for ($i = 1; $i <= 14; $i++) {
$liste[$i] = 0;
}
$r2 = $r * $r;
$fein = 1000000000;
for ($i = 1; $i <= $n; $i++) {
$x = mt_rand(0, $fein) / $fein;
$y = mt_rand(0, $fein) / $fein;
$minx = -intval($r - $x);
$maxx = intval($r + $x);
$miny = -intval($r - $y);
$maxy = intval($r + $y);
$unter = 0;
for ($j = $minx; $j <= $maxx; $j++) {
for ($k = $miny; $k <= $maxy; $k++) {
$dx = $j - $x;
$dy = $k - $y;
$d = $dx * $dx + $dy * $dy;
if ($d < $r2) {
$unter++;
}
}
}
$liste[$unter] ++;
}
return $liste;
}
Programm 1
Das Ergebnis ist in den beiden folgenden Tabellen zusammengefasst:
| Kreisradius = 1 | ||||||
|---|---|---|---|---|---|---|
| Gitterpunkte | 1. Durchgang | 2. Durchgang | 3. Durchgang | 4. Durchgang | 5. Durchgang | % Anteil |
| 2 | 17300 | 17287 | 17011 | 17367 | 17252 | 17,243400% |
| 3 | 51028 | 51036 | 51458 | 51211 | 51126 | 51,171800% |
| 4 | 31672 | 31677 | 31531 | 31422 | 31622 | 31,584800% |
| gewichtetes Mittel | 12 ⋅ 3,143414000000000 | |||||
Tabelle 1
| Kreisradius = 2 | ||||||
|---|---|---|---|---|---|---|
| Gitterpunkte | 1. Durchgang | 2. Durchgang | 3. Durchgang | 4. Durchgang | 5. Durchgang | % Anteil |
| 10 | 1172 | 1195 | 1197 | 1179 | 1230 | 1,194600% |
| 11 | 17508 | 17573 | 17572 | 17536 | 17719 | 17,581600% |
| 12 | 22126 | 21952 | 22044 | 21972 | 22184 | 22,055600% |
| 13 | 41427 | 41810 | 41810 | 41839 | 41292 | 41,635600% |
| 14 | 17767 | 17470 | 17377 | 17474 | 17575 | 17,532600% |
| gewichtetes Mittel | 22 ⋅ 3,141824999999999 | |||||
Tabelle 2
Trotz der riesigen Anzahl von 2 mal 500.000 Zufallspositionen für beide Tabellen ist das Ergebnis für das gewichtete Mittel dürftig. Auch wenn man das Programm noch weiter beschleunigt und die Laufzeit drastisch erhöht, wird es immer noch nicht wirklich gut. Mit einem externen Compiler, der hundertfach schneller arbeitet, und einer Laufzeit von mehr als einem Tag lagen die folgenden Ergebnisse vor:
| Kreisradius = 1 | ||
|---|---|---|
| Gitterpunkte | Anzahl | % Anteil |
| 2 | 173553705203 | 17,3553705203 |
| 3 | 511298960180 | 51,1298960180 |
| 4 | 315147334617 | 31,5147334617 |
| gewichtetes Mittel | 12 ⋅ 3,1415936947 | |
Tabelle 3
| Kreisradius = 2 | ||
|---|---|---|
| Gitterpunkte | Anzahl | % Anteil |
| 10 | 1216780575 | 1,216780575 |
| 11 | 17655794485 | 17,655794485 |
| 12 | 21981840224 | 21,981840224 |
| 13 | 41564759523 | 41,564759523 |
| 14 | 17580825193 | 17,580825193 |
| gewichtetes Mittel | 22 ⋅ 3,141592741025 | |
Tabelle 4
Ein riesiger Zeitaufwand und gerade mal 6 Nachkommastellen bei $\pi$. Eine Verbesserung um eine weitere Stelle würde den Zeitaufwand verhundertfachen.
Sicherlich wäre das obige Ergebnis noch gerade als ausreichend "genaue" Lösung anzusehen, aber sehr befriedigend ist das nicht.
2.) mathematische Lösung für r = 1
Das folgende Bild 1 mit 500 x 500 = 250000 farbigen Pixel ist eine andere Form von Ergebnis eines Durchlaufs. Es sind die Bedeckungszahlen als Farben dargestellt und es sind keine Zufallspositionen (bei denen man nach beliebiger Anzahl aufhören kann) sondern Rasterpunkte innerhalb der Fläche eines Einheitsquadrats (bei dem man zwar mit kleinerer Auflösung, aber immer bis zum Ende durchhalten muss). Wichtig ist das Erkennen von Kreisbögen, und die Pixel-Auflösung muss nur diese ausreichend deutlich zeigen.Die Farbzuordnung zu den Bedeckungszahlen sind: 2 (violet) 3 (green) 4 (yellow)

|
Bild 1
Die Lösung des Rätsels läuft nun auf eine Flächenberechnung hinaus, wobei die gesamte Quadratfläche gleich 100% ist. Die Auflösung des Bildes spielt dann keine Rolle mehr, denn man geht von idealen Kreisbögen aus, auch wenn im Bild Pixel-Treppen zu sehen sind. Die Mittelpunkte aller Kreise liegen immer auf Gitterpunkten, in diesem ersten Fall auf den Eckpunkten des Bildes.
Für die Berechnungen (und insbesondere weiter unten für $r=2$) sind einige einfache Formel zu benutzen: $$ \text{Abstand zweier Punkte }P_1(x_1\;|\;x_2)\text{ und }P_2(x_2\;|\;x_2):\quad d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\tag{1}$$ $$ \text{Dreiecksfläche}:\quad F_{△}=\sqrt {s\cdot (s-a)\cdot (s-b)\cdot (s-c)}\quad\text{mit}\quad s={\frac {a+b+c}{2}}\tag{2} $$ $$ \text{Kreisabschnitt über d}:\quad F_d=\frac {r^2}{2}\cdot (\alpha -\sin \alpha ) \quad\text{mit}\quad \alpha =2\cdot \arcsin \left(\frac {d}{2r}\right)\tag{3} $$ Dabei sind $a$, $b$ und $c$ Dreieckseiten und $d$ eine Dreiecks- oder Rechteckseite mit Krümmung, die flächenkorrigiert werden muss. Der Radius $r$ ist der bekannte Radius des Bedeckungskreises.
Bei Bild 1 ist die Flächenberechnung sehr einfach: es werden die Koordinaten von zwei benachbarten Eckpunkten der gelben Fläche und damit deren Abstand $d$ berechnet. Damit ist die Fläche des Quadrats im Inneren der gelben Fläche $d\cdot d$ bekannt und um die gesamte gelbe Fläche zu berechnen, muss noch 4 mal der Kreisabschnitt über $d$ addiert werden.
Die Koordinaten sind folgendermaßen zu verstehen: $$\begin{alignat}{1} \text{linke untere Bildecke}\quad P_1=&(x_1\;|\;y_1)=(0\;|\;0) \\ \text{rechte untere Bildecke}\quad P_2=&(x_2\;|\;y_2)=(1\;|\;0) \\ \text{rechte obere Bildecke}\quad P_3=&(x_3\;|\;y_3)=(1\;|\;1) \\ \text{linke obere Bildecke}\quad P_4=&(x_4\;|\;y_4)=(0\;|\;1) \\ \text{oberer Eckpunkt der gelben Fläche}\quad P_5=&(x_5\;|\;y_5)=(1/2\;|\;\sqrt{3}/2) \\ \text{rechter Eckpunkt der gelben Fläche}\quad P_6=&(x_6\;|\;y_6)=(\sqrt{3}/2\;|\;1/2) \\ \text{Kantenlänge des gelben Quadrats}\quad d =& \sqrt{(x_5-x_6)^2+(y_5-y_6)^2} \\ d =& \sqrt{2-\sqrt{3}}=0,51763809020504 \\ \text{Mittelpunktswinkel}\quad\alpha=& 0,52359877559830 \\ \text{Kreisabschnitt an }d\quad F_d =& 0,01179938779915 \\ \end{alignat}$$ $$ \rand{\text{gelbe Fläche}\quad F_4 = d^2+4\cdot F_d = 0,31514674362772=31,51467436277206\,\%} \\ $$ $$\begin{alignat}{1} \text{Quadrat - Viertelkreis } =& \text{ halbe violette Fläche + viertel grüne Fläche} \\ 1^2-\pi/4 =& 1/2\cdot F_2+1/4\cdot F_3 \\ \pi/4 =& 1/2\cdot F_2+3/4\cdot F_3+F_4 \end{alignat}$$ Die untere Gleichung wird von der oberen abgezogen und die resultierende Gleichung nach $F_3$ aufgelöst: $$ \rand{\text{grüne Fläche}\quad F_3 = \pi-2-2\cdot F_4 = 0,51129916633435=51,12991663343519\,\%} \\ \rand{\text{violette Fläche}\quad F_2 = 1-F_3-F_4 = 0,17355409003793=17,35540900379275\,\%} \\ \\ \text{Test auf Übereinstimmung mit }\pi:\quad Test = \frac{2\cdot F_2+3\cdot F_3+4\cdot F_4}{1\cdot1}=3,14159265358979 $$ Damit ist die erste Rätselfrage beantwortet.
3.) mathematische Lösung für r = 2
Das folgende Bild 2 ist auf gleiche Weise wie Bild 1 entstanden, nur mit $r=2$.Die Farbzuordnung zu den Bedeckungszahlen sind: 10 (indigo) 11 (orange) 12 (blue) 13 (red) 14 (violet)

|
Bild 2
Die Farbflächen sind viel komplexer aufgebaut und die Kreisbögen mit Radius=2 sowie deren Mittelpunkte sind nicht leicht zu erkennen. Deshalb gibt es ein Bild 3 als Orientierungshilfe, dessen oberes linkes Viertel mit Bild 2 verkleinert übereinstimmt, aber zusätzlich weitere Kopien rechts und unten zeigt. Damit lassen sich besser die Koordinaten der Kreismittelpunkte bestimmen. Diese liegen immer auf den Gitterpunkten: bei Bild 2 an allen vier Ecken und bei Bild 3 sind es neun Punkte, acht auf dem Rand und einer in der Mitte.

|
Bild 3
Aber wegen der Symmetrie ist zur Flächenberechnung nur ein kleiner Ausschnitt von Bild 2 erforderlich, nämlich ein achtel der Fläche. Bild 4 zeigt diesen Ausschnitt und zusätzlich die zur Flächenberechnung erforderlichen Punkte.

|
Bild 4
Die nun abschließende Aufgabe ist:
- Bestimmung der Punktkoordinaten bezogen auf einen beliebigen Fixpunkt z.B. $P_0(0\;|\;1/2)$
- Längenbestimmung (Punktabstand) von auch gekrümmten Dreieckseiten
- Flächenberechnungen je Farbe für Dreiecke und Kreisabschnitte wie schon für Bild 1
4.) Punktkoordinaten-Berechnung von Kreisschnittpunkten
Am Beispiel von $P_8$ soll gezeigt werden, wie die Koordinaten in Bild 4 berechnet werden.Das folgende Bild 5 zeigt ein großes hellgraues Quadrat, welches dem Bild 3 entspricht. Das kleine graue Quadrat entspricht dem Bild 2 und das dunkelgraue Dreieck dem Bild 4.
Bild 5
Der Punkt $P_8$ ist einer der beiden Schnittpunkte der Kreise mit den Mittelpunkten bei $M_1=(1\;|\;-1)$ und $M_2=(2\;|\;0)$. Die x- und y-Koordinaten werden für die Berechnung im Weiteren getrennt behandelt, also $$ x(M_1)=1 \\ y(M_1)=-1 \\ x(M_2)=2 \\ y(M_2)=0 \\ x(M)=\frac{x(M_1)+x(M_2)}{2}=3/2 \\ y(M)=\frac{y(M_1)+y(M_2)}{2}=-1/2 \\ dx=|x(M_1)-x(M)|=1/2 \\ dy=|y(M_1)-y(M)|=1/2 \\ d^2=dx^2+dy^2=1/2 \\ d=+\sqrt{1/2} \\ s^2=r^2-d^2=7/2 \\ s=+\sqrt{7/2} \\ sx/s=dy/d=\sin{\epsilon} \\ sy/s=dx/d=\cos{\epsilon} \\ sx=s\cdot dy/d=\sqrt{7/2}\cdot (1/2)/\sqrt{1/2}=1/2\cdot\sqrt{7} \\ sy=s\cdot dx/d=\sqrt{7/2}\cdot (1/2)/\sqrt{1/2}=1/2\cdot\sqrt{7} \\ x(P_8)=x(M)∓sx=3/2∓1/2\cdot\sqrt{7} \\ y(P_8)=y(M)±sy=-1/2±1/2\cdot\sqrt{7} \\ \sand{P_8=((3-\sqrt{7})/2\;|\;(\sqrt{7}-1)/2)=(0,17712434446771\;|\;0,82287565553230)} \\ {P_8}'=((3+\sqrt{7})/2\;|\;(-\sqrt{7}-1)/2)=(2,82287565553230\;|\;-1,82287565553230) $$ Ein kleines Programm oder eine EXCEL-Tabelle kann die obigen Schritte zusammenfassen und damit auch für die anderen Punkte eine schnelle Berechnung ermöglichen. Da es zwei Schnittpunkte gibt, muss immer derjenige gewählt werden, der in dem durch Bild 4 festgelegten Flächenbereich liegt, also $0≤x≤0,5$ und $0,5≤y≤1$.
| Punkt | Mittelpunkte von | Punktkoordinaten | |||
|---|---|---|---|---|---|
| Nr. | Kreis 1 | Kreis 2 | x | y | |
| $ P_{0}$ | $\Big{(}0\;|\;1/2\Big{)}$ | $0,00000000000000$ | $0,50000000000000$ | ||
| $ P_{1}$ | $\Big{(}0\;|\;1\Big{)}$ | $0,00000000000000$ | $1,00000000000000$ | ||
| $ P_{2}$ | $\Big{(}2\;|\;0\Big{)}$ | $\Big{(}2\;|\;2\Big{)}$ | $\Big{(}2-\sqrt{3}\;|\;1\Big{)}$ | $0,26794919243112$ | $1,00000000000000$ |
| $ P_{3}$ | $\Big{(}1/2\;|\;1\Big{)}$ | $0,50000000000000$ | $1,00000000000000$ | ||
| $ P_{4}$ | $\Big{(}0\;|\;-1\Big{)}$ | $\Big{(}1\;|\;-1\Big{)}$ | $\Big{(}1/2\;|\;\sqrt{15/4}-1\Big{)}$ | $0,50000000000000$ | $0,93649167310371$ |
| $ P_{5}$ | $\Big{(}-1\;|\;2\Big{)}$ | $\Big{(}2\;|\;2\Big{)}$ | $\Big{(}1/2\;|\;2-\sqrt{7/4}\Big{)}$ | $0,50000000000000$ | $0,67712434446771$ |
| $ P_{6}$ | $\Big{(}1/2\;|\;1/2\Big{)}$ | $0,50000000000000$ | $0,50000000000000$ | ||
| $ P_{7}$ | $\Big{(}-1\;|\;2\Big{)}$ | $\Big{(}\sqrt{2}-1\;|\;2-\sqrt{2}\Big{)}$ | $0,41421356237310$ | $0,58578643762691$ | |
| $ P_{8}$ | $\Big{(}1\;|\;-1\Big{)}$ | $\Big{(}2\;|\;0\Big{)}$ | $\Big{(}(3-\sqrt{7})/2\;|\;(\sqrt{7}-1)/2\Big{)}$ | $0,17712434446771$ | $0,82287565553230$ |
| $ P_{9}$ | $\Big{(}0\;|\;-1\Big{)}$ | $\Big{(}2\;|\;0\Big{)}$ | $\Big{(}(2-\sqrt{11/5})/2\;|\;\sqrt{11/5}-1/2\Big{)}$ | $0,25838015129043$ | $0,98323969741913$ |
| $ P_{10}$ | $\Big{(}0\;|\;-1\Big{)}$ | $\Big{(}2\;|\;2\Big{)}$ | $\Big{(}1-3/2\cdot\sqrt{3/13}\;|\;1/2+\sqrt{3/13}\Big{)}$ | $0,27942330787711$ | $0,98038446141526$ |
| $ P_{11}$ | $\Big{(}1\;|\;-1\Big{)}$ | $\Big{(}2\;|\;2\Big{)}$ | $\Big{(}3/2\cdot(1-\sqrt{3/5})\;|\;1/2\cdot(1+\sqrt{3/5})\Big{)}$ | $0,33810499613778$ | $0,88729833462074$ |
Bei den Punkten ohne Kreismittelpunkte ist kein Schnittpunkt erforderlich, denn die Koordinaten sind offensichtlich. Bei Punkt $P_7$ ist der Schnittpunkt von Kreis 1 mit der Strecke $\overline{P_1P_6}$ leicht zu berechnen.
5.) Berechnung der farbigen Flächen
Nun lassen sich leicht die Flächen der Dreiecke einschließlich der Seitenkrümmung berechnen. Die so erhaltenen Flächen aufsummiert nach Farben müssen mit 8 multipliziert werden um die gesamten Teilflächen auf dem Bild 2 zu beinhalten.Am Beispiel einer einzelnen Fläche wird nun die Vorgehensweise gezeigt.
Das Flächenstück in indigo hat die Eckpunkte $P_1$, $P_2$ und $P_9$. Diese Fläche ist durch eine gerade Linie von $P_1$ nach $P_2$ begrenzt und zwei gekrümmte Begrenzungen mit nach innen gekrümmten Kreisbögen. Zunächst wird die reine Dreiecksfläche bestimmt. Dazu sind die drei Seitenlängen zu berechnen. Das geschieht mit der Formel (1) oben: $$ a=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}=0,26794919243112 \\ b=\sqrt{(x_1-x_9)^2+(y_1-y_9)^2}=0,25892317455854 \\ c=\sqrt{(x_2-x_9)^2+(y_2-y_9)^2}=0,01929959302562 $$ Die Dreiecksfläche wird nach Formel (2) berechnet: $$ s={\frac {a+b+c}{2}}=0,27308598000764 \\ F_{△(1,2,9)}=\sqrt {s\cdot (s-a)\cdot (s-b)\cdot (s-c)}=0,00224545477072 $$ Nun müssen bei Seite b und c die Flächen der Kreisabschnitte nach Formel (3) abgezogen werden: $$ \alpha_b =2\cdot \arcsin \left(\frac {b}{2r}\right)=0,12955216714882 \\ \alpha_c =2\cdot \arcsin \left(\frac {c}{2r}\right)=0,00964983395384 \\ F_b=\frac {r^2}{2}\cdot (\alpha_b -\sin \alpha_b )=0,00072418300721 \\ F_c=\frac {r^2}{2}\cdot (\alpha_c -\sin \alpha_c )=0,00000029952718 \\ 1/8\cdot F_{10 indigo}=F_{△(1,2,9)}-F_b-F_c=0,00152097223633 \\ \rand{F_{10 indigo}=0,01216777789061=1,21677778906082\,\%} $$ Nach dem gleichen Prinzip werden nun die übrigen Flächen berechnet und nach Farben zusammengefasst. Nur bei rot kann man sich die Arbeit sparen, weil man einfach die Ergänzung zum vollen Quadrat dafür einsetzen kann. Zudem müsste man noch das Viereck in zwei Dreiecke zerlegen. Wer das mal überprüfen will kann genauso vorgehen wie für die anderen Farben. $$ F_{11 orange_a}=0,17504259198377 \\ F_{11 orange_b}=0,00151533816838 \\ \rand{F_{11 orange}=0,17655793015215=17,65579301521475\,\%} \\ F_{12 blue_a}=0,06012341746171 \\ F_{12 blue_b}=0,07044945546034 \\ F_{12 blue_c}=0,08924645497994 \\ \rand{F_{12 blue}=0,21981932790198=21,98193279019837\,\%} \\ \rand{F_{14 violet}=0,17580913623728=17,58091362372767\,\%} \\ \rand{F_{13 red}=0,41564582781798=41,56458278179839\,\%} \\ \\ \text{Test auf Übereinstimmung mit }\pi:\quad Test=\frac{10\cdot F_{10}+11\cdot F_{11}+12\cdot F_{12}+13\cdot F_{13}+14\cdot F_{14}}{2\cdot 2}=3,14159265358979 $$
Damit ist die zweite und letzte Rätselfrage beantwortet.
6.) über das Rätsel hinaus: Probleme mit r = 3, 5 und 10
Wenn man sich die Steigerung der Schwierigkeiten von $r=1$ zu $r=2$ vergegenwärtigt, werden die noch größeren Probleme einer exakten Lösung bei $r>2$ bewusst. Die entsprechenden Bilder für 3, 5 und 10 sehen so aus:



|
Bild 6
Solche Flächen nach dem obigen Prinzip für jede Farbe zu berechnen ist zwar nicht unmöglich, aber sehr aufwändig. Da bleibt dann nur die statistische Methode mit der damit verbundenen Ungenauigkeit.
| Kreisradius = 3 | Kreisradius = 5 | Kreisradius = 10 | |||
|---|---|---|---|---|---|
| Gitterpunkte | % Anteil | Gitterpunkte | % Anteil | Gitterpunkte | % Anteil |
| 26 (violet) | 5,274818777 | 74 (violet) | 0,09843880 | 308 (aqua) | 0,04925708 |
| 27 (green) | 17,555304705 | 75 (green) | 3,36617580 | 309 (gold) | 0,64887045 |
| 28 (yellow) | 36,395944841 | 76 (yellow) | 2,94118667 | 310 (indigo) | 1,69389321 |
| 29 (cyan) | 31,672743005 | 77 (cyan) | 12,89421699 | 311 (orange) | 7,45360947 |
| 30 (brown) | 5,861259542 | 78 (brown) | 26,66294722 | 312 (blue) | 13,73616330 |
| 31 (gray) | 0,817054278 | 79 (gray) | 30,44291781 | 313 (red) | 18,16303531 |
| 32 (aqua) | 2,422874852 | 80 (aqua) | 17,97456695 | 314 (violet) | 11,02045285 |
| 81 (gold) | 5,61954976 | 315 (green) | 14,60718105 | ||
| 316 (yellow) | 20,74050170 | ||||
| 317 (cyan) | 9,39862211 | ||||
| 318 (brown) | 2,48458720 | ||||
| 319 (gray) | 0,00382627 | ||||
| 32 ⋅ 3,141592237689 | 52 ⋅ 3,141592712404 | 102 ⋅ 3,141593017578 | |||
| 46396,355 s = 12,89 h | 11822,787 s = 3,28 h | 36855,504 s = 10,24 h | |||
Tabelle 5
Die vorletzte Zeile gibt den gewichteten Mittelwert an und die letzte Zeile die Laufzeit des schnellen compilierten Programms wie oben schon erwähnt. Es sind 100.000.000.000 Zufallspunkte bei $r=3$, 10.000.000.000 Zufallspunkte bei $r=5$ und 10.000.000.000 Zufallspunkte bei $r=10$ berechnet und jeweils dabei die unter der Kreisfläche liegenden Gitterpunkte gezählt worden. Trotz dieser hohen Zahlen sind die Genauigkeiten bestenfalls auf 6 Nachkommastellen richtig.
7.) kleine nicht ganzzahlige Radien
Bei den großen Radien wird die Problemlösung immer komplexer. Daher ist es interessant, mit kleinen Radien beherrschbare Möglichkeiten zu finden. Es bieten sich Radien an, die nur geringe Zahlen von Gitterpunkten bedecken. Ein erster Test ist $r=1/2$
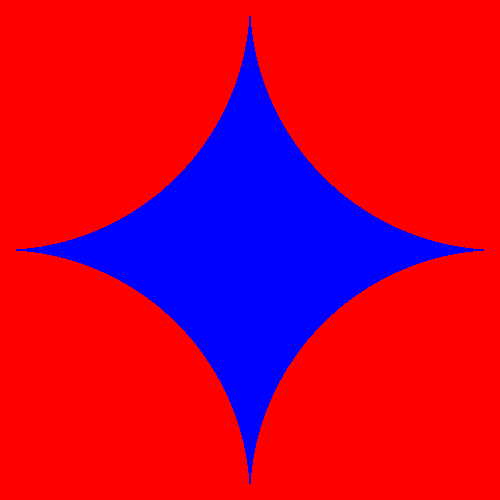
|
Bild 7
Hier kommen nur die Bedeckungszahlen 0 (blue) und 1 (red) vor. Dabei ist es nicht einmal erforderlich die Flächen von Bild 7 zu berechnen, obwohl das sehr einfach ist. Bei nur zwei unterschiedlichen Bedeckungspunktenzahlen ist eine einfache Rechnung von zwei Gleichungen mit zwei Unbekannten möglich: $$ p_0 + p_1 = 1 \\ 0\cdot p_0+1\cdot p_1=1/2\cdot 1/2\cdot \pi=\pi/4 \\ \rand{p_1=\pi/4=0,78539816339745=78,53981633974483\,\%} \\ \rand{p_0=1-p_1=0,21460183660255=21,46018366025517\,\%} $$ Man kann sich auch mal den irrationalen Radius $\sqrt{2}/2=0,70710678118655$ vornehmen:

|
Bild 8
Hier kommen nur die Bedeckungszahlen 1 (red) und 2 (violet) vor. Deshalb auch hier zwei Gleichungen mit zwei Unbekannten: $$ p_1 + p_2 = 1 \\ 1\cdot p_1+2\cdot p_2=\pi/2 \\ \rand{p_2=\pi/2-1=0,57079632679490=57,07963267948966\,\%} \\ \rand{p_1=1-p_2=0,42920367320510=42,92036732051034\,\%} $$