Da es sich hier aber um 34 mögliche Summanden handelt ist die Zahl der Kombinationen recht hoch. Jeder Summand kann entweder an der Summe beteiligt oder nicht beteiligt sein, also gibt es zwei Möglichkeiten und das für jeden der 34 Summanden. Es ergibt sich die Zahl von $$2^{34}=17.179.869.184\;\text{Möglichkeiten}$$ und da stellt sich schon die Frage, ob man das selbst mit Rechnerunterstützung innerhalb vernünftiger Zeit schaffen kann. Das würde z.B. bedeuten, dass beim Testen von 1000 Möglichkeiten pro Sekunde ein Rechner immer noch 198,84 Tage benötigen würde.
Versuchen wir die Zahl der Möglichkeiten zunächst etwas einzuschränken. Wenn man sich fragt, wie viele Summanden sich in der geforderten Summe von 1.900.968,61 Euro befinden dürfen stellt man folgendes fest:
| Teilsumme = 1.900.968,61 Euro | ||
|---|---|---|
| minimale Anzahl der Summanden | ||
| Nr. | Summanden absteigend | Teilsumme bis zur jeweiligen Zeile |
| 1 | 664.949,21 | 664.949,21 |
| 2 | 303.618,05 | 968.567,26 |
| 3 | 168.451,78 | 1.137.019,04 |
| 4 | 137.410,88 | 1.274.429,92 |
| 5 | 124.348,02 | 1.398.777,94 |
| 6 | 88.244,85 | 1.487.022,79 |
| 7 | 77.275,02 | 1.564.297,81 |
| 8 | 66.508,92 | 1.630.806,73 |
| 9 | 61.875,01 | 1.692.681,74 |
| 10 | 53.121,77 | 1.745.803,51 |
| 11 | 42.078,38 | 1.787.881,89 |
| 12 | 39.820,65 | 1.827.702,54 |
| 13 | 39.111,00 | 1.866.813,54 |
| 14 | 35.281,35 | 1.902.094,89 |
| 15 | 23.542,38 | 1.925.637,27 |
| 16 | 21.907,34 | 1.947.544,61 |
| 17 | 19.294,52 | 1.966.839,13 |
| 18 | 18.086,50 | 1.984.925,63 |
| 19 | 17.221,91 | 2.002.147,54 |
| 20 | 14.887,04 | 2.017.034,58 |
| 21 | 12.440,91 | 2.029.475,49 |
| 22 | 11.677,53 | 2.041.153,02 |
| 23 | 10.075,03 | 2.051.228,05 |
| 24 | 9.970,44 | 2.061.198,49 |
| 25 | 9.739,13 | 2.070.937,62 |
| 26 | 9.296,69 | 2.080.234,31 |
| 27 | 7.785,22 | 2.088.019,53 |
| 28 | 7.785,20 | 2.095.804,73 |
| 29 | 7.479,76 | 2.103.284,49 |
| 30 | 6.767,42 | 2.110.051,91 |
| 31 | 6.667,42 | 2.116.719,33 |
| 32 | 6.314,44 | 2.123.033,77 |
| 33 | 6.170,52 | 2.129.204,29 |
| 34 | 4.528,07 | 2.133.732,36 |
| Teilsumme = 1.900.968,61 Euro | ||
|---|---|---|
| maximale Anzahl der Summanden | ||
| Nr. | Summanden aufsteigend | Teilsumme bis zur jeweiligen Zeile |
| 1 | 4.528,07 | 4.528,07 |
| 2 | 6.170,52 | 10.698,59 |
| 3 | 6.314,44 | 17.013,03 |
| 4 | 6.667,42 | 23.680,45 |
| 5 | 6.767,42 | 30.447,87 |
| 6 | 7.479,76 | 37.927,63 |
| 7 | 7.785,20 | 45.712,83 |
| 8 | 7.785,22 | 53.498,05 |
| 9 | 9.296,69 | 62.794,74 |
| 10 | 9.739,13 | 72.533,87 |
| 11 | 9.970,44 | 82.504,31 |
| 12 | 10.075,03 | 92.579,34 |
| 13 | 11.677,53 | 104.256,87 |
| 14 | 12.440,91 | 116.697,78 |
| 15 | 14.887,04 | 131.584,82 |
| 16 | 17.221,91 | 148.806,73 |
| 17 | 18.086,50 | 166.893,23 |
| 18 | 19.294,52 | 186.187,75 |
| 19 | 21.907,34 | 208.095,09 |
| 20 | 23.542,38 | 231.637,47 |
| 21 | 35.281,35 | 266.918,82 |
| 22 | 39.111,00 | 306.029,82 |
| 23 | 39.820,65 | 345.850,47 |
| 24 | 42.078,38 | 387.928,85 |
| 25 | 53.121,77 | 441.050,62 |
| 26 | 61.875,01 | 502.925,63 |
| 27 | 66.508,92 | 569.434,55 |
| 28 | 77.275,02 | 646.709,57 |
| 29 | 88.244,85 | 734.954,42 |
| 30 | 124.348,02 | 859.302,44 |
| 31 | 137.410,88 | 996.713,32 |
| 32 | 168.451,78 | 1.165.165,10 |
| 33 | 303.618,05 | 1.468.783,15 |
| 34 | 664.949,21 | 2.133.732,36 |
Es müssen also mehr als 13 Summanden und weniger als 34 Summanden sein, ansonsten kann die geforderte Teilsumme mit den vorgegebenen Summanden nicht erreicht werden. Das ergibt sich daraus, das beim Aufsummieren der größten Summanden erst bei 14 die geforderte Summe überschritten wird. Entsprechend ist beim Aufsummieren der kleinsten Summanden eine Überschreitung der geforderten Summe erst mit 34 erreicht.
Nun kann man aber auch nach den Summanden fragen, die die Differenz aus Summe und Teilsumme bilden, also nach der noch ausstehenden Zahlung. Wenn man diese kennt sind auch die ursprünglich gesuchten bekannt. Also ist wie bei den obigen Tabellen zu prüfen, wie viele Summanden maximal und minimal in Frage kommen, diesmal aber für den Betrag von 232.763,75 Euro.
| Restsumme 232.763,75 Euro | ||
|---|---|---|
| minimale Anzahl der Summanden | ||
| Nr. | Summanden absteigend | Teilsumme bis zur jeweiligen Zeile |
| 1 | 664.949,21 | 664.949,21 |
| 2 | 303.618,05 | 968.567,26 |
| 3 | 168.451,78 | 1.137.019,04 |
| 4 | 137.410,88 | 1.274.429,92 |
| 5 | 124.348,02 | 1.398.777,94 |
| 6 | 88.244,85 | 1.487.022,79 |
| 7 | 77.275,02 | 1.564.297,81 |
| 8 | 66.508,92 | 1.630.806,73 |
| 9 | 61.875,01 | 1.692.681,74 |
| 10 | 53.121,77 | 1.745.803,51 |
| 11 | 42.078,38 | 1.787.881,89 |
| 12 | 39.820,65 | 1.827.702,54 |
| 13 | 39.111,00 | 1.866.813,54 |
| 14 | 35.281,35 | 1.902.094,89 |
| 15 | 23.542,38 | 1.925.637,27 |
| 16 | 21.907,34 | 1.947.544,61 |
| 17 | 19.294,52 | 1.966.839,13 |
| 18 | 18.086,50 | 1.984.925,63 |
| 19 | 17.221,91 | 2.002.147,54 |
| 20 | 14.887,04 | 2.017.034,58 |
| 21 | 12.440,91 | 2.029.475,49 |
| 22 | 11.677,53 | 2.041.153,02 |
| 23 | 10.075,03 | 2.051.228,05 |
| 24 | 9.970,44 | 2.061.198,49 |
| 25 | 9.739,13 | 2.070.937,62 |
| 26 | 9.296,69 | 2.080.234,31 |
| 27 | 7.785,22 | 2.088.019,53 |
| 28 | 7.785,20 | 2.095.804,73 |
| 29 | 7.479,76 | 2.103.284,49 |
| 30 | 6.767,42 | 2.110.051,91 |
| 31 | 6.667,42 | 2.116.719,33 |
| 32 | 6.314,44 | 2.123.033,77 |
| 33 | 6.170,52 | 2.129.204,29 |
| 34 | 4.528,07 | 2.133.732,36 |
| Restsumme 232.763,75 Euro | ||
|---|---|---|
| maximale Anzahl der Summanden | ||
| Nr. | Summanden aufsteigend | Teilsumme bis zur jeweiligen Zeile |
| 1 | 4.528,07 | 4.528,07 |
| 2 | 6.170,52 | 10.698,59 |
| 3 | 6.314,44 | 17.013,03 |
| 4 | 6.667,42 | 23.680,45 |
| 5 | 6.767,42 | 30.447,87 |
| 6 | 7.479,76 | 37.927,63 |
| 7 | 7.785,20 | 45.712,83 |
| 8 | 7.785,22 | 53.498,05 |
| 9 | 9.296,69 | 62.794,74 |
| 10 | 9.739,13 | 72.533,87 |
| 11 | 9.970,44 | 82.504,31 |
| 12 | 10.075,03 | 92.579,34 |
| 13 | 11.677,53 | 104.256,87 |
| 14 | 12.440,91 | 116.697,78 |
| 15 | 14.887,04 | 131.584,82 |
| 16 | 17.221,91 | 148.806,73 |
| 17 | 18.086,50 | 166.893,23 |
| 18 | 19.294,52 | 186.187,75 |
| 19 | 21.907,34 | 208.095,09 |
| 20 | 23.542,38 | 231.637,47 |
| 21 | 35.281,35 | 266.918,82 |
| 22 | 39.111,00 | 306.029,82 |
| 23 | 39.820,65 | 345.850,47 |
| 24 | 42.078,38 | 387.928,85 |
| 25 | 53.121,77 | 441.050,62 |
| 26 | 61.875,01 | 502.925,63 |
| 27 | 66.508,92 | 569.434,55 |
| 28 | 77.275,02 | 646.709,57 |
| 29 | 88.244,85 | 734.954,42 |
| 30 | 124.348,02 | 859.302,44 |
| 31 | 137.410,88 | 996.713,32 |
| 32 | 168.451,78 | 1.165.165,10 |
| 33 | 303.618,05 | 1.468.783,15 |
| 34 | 664.949,21 | 2.133.732,36 |
Es gibt keine untere Schranke für die Anzahl der Summanden aber es sind weniger als 21. Die nicht vorhandene untere Schranke bedeutet, das bereits einer der großen Summanden zu viel ist. Das werden wir gleich noch genauer bewerten.
Die Berechnung der Möglichkeiten für eine feste Anzahl von Summanden läuft auf die Berechnung der Binomial-Koeffizienten hinaus. Bekannt sind diese Zahlen aus dem Pascalschen Dreieck:
| 1 | ||||||||
| 1 | 1 | |||||||
| 1 | 2 | 1 | ||||||
| 1 | 3 | 3 | 1 | |||||
| 1 | 4 | 6 | 4 | 1 |
Die 34. Zeile (beginnend bei Null) hat die folgenden Zahlenwerte:
| Teilsumme = 1.900.968,61 Euro | ||
|---|---|---|
| Binomial-Koeffizienten der 34. Zeile | ||
| Spalte oder Summandenzahl | Formel Darstellung | Zahl der Möglichkeiten |
| 0 | $0\choose{34}$ | 1 |
| 1 | $1\choose{34}$ | 34 |
| 2 | $2\choose{34}$ | 561 |
| 3 | $3\choose{34}$ | 5.984 |
| 4 | $4\choose{34}$ | 46.376 |
| 5 | $5\choose{34}$ | 278.256 |
| 6 | $6\choose{34}$ | 1.344.904 |
| 7 | $7\choose{34}$ | 5.379.616 |
| 8 | $8\choose{34}$ | 18.156.204 |
| 9 | $9\choose{34}$ | 52.451.256 |
| 10 | $10\choose{34}$ | 131.128.140 |
| 11 | $11\choose{34}$ | 286.097.760 |
| 12 | $12\choose{34}$ | 548.354.040 |
| 13 | $13\choose{34}$ | 927.983.760 |
| 14 | $14\choose{34}$ | 1.391.975.640 |
| 15 | $15\choose{34}$ | 1.855.967.520 |
| 16 | $16\choose{34}$ | 2.203.961.430 |
| 17 | $17\choose{34}$ | 2.333.606.220 |
| 18 | $18\choose{34}$ | 2.203.961.430 |
| 19 | $19\choose{34}$ | 1.855.967.520 |
| 20 | $20\choose{34}$ | 1.391.975.640 |
| 21 | $21\choose{34}$ | 927.983.760 |
| 22 | $22\choose{34}$ | 548.354.040 |
| 23 | $23\choose{34}$ | 286.097.760 |
| 24 | $24\choose{34}$ | 131.128.140 |
| 25 | $25\choose{34}$ | 52.451.256 |
| 26 | $26\choose{34}$ | 18.156.204 |
| 27 | $27\choose{34}$ | 5.379.616 |
| 28 | $28\choose{34}$ | 1.344.904 |
| 29 | $29\choose{34}$ | 278.256 |
| 30 | $30\choose{34}$ | 46.376 |
| 31 | $31\choose{34}$ | 5.984 |
| 32 | $32\choose{34}$ | 561 |
| 33 | $33\choose{34}$ | 34 |
| 34 | $34\choose{34}$ | 1 |
| Restsumme 232.763,75 Euro | ||
|---|---|---|
| Binomial-Koeffizienten der 34. Zeile | ||
| Spalte oder Summandenzahl | Formel Darstellung | Zahl der Möglichkeiten |
| 0 | $0\choose{34}$ | 1 |
| 1 | $1\choose{34}$ | 34 |
| 2 | $2\choose{34}$ | 561 |
| 3 | $3\choose{34}$ | 5.984 |
| 4 | $4\choose{34}$ | 46.376 |
| 5 | $5\choose{34}$ | 278.256 |
| 6 | $6\choose{34}$ | 1.344.904 |
| 7 | $7\choose{34}$ | 5.379.616 |
| 8 | $8\choose{34}$ | 18.156.204 |
| 9 | $9\choose{34}$ | 52.451.256 |
| 10 | $10\choose{34}$ | 131.128.140 |
| 11 | $11\choose{34}$ | 286.097.760 |
| 12 | $12\choose{34}$ | 548.354.040 |
| 13 | $13\choose{34}$ | 927.983.760 |
| 14 | $14\choose{34}$ | 1.391.975.640 |
| 15 | $15\choose{34}$ | 1.855.967.520 |
| 16 | $16\choose{34}$ | 2.203.961.430 |
| 17 | $17\choose{34}$ | 2.333.606.220 |
| 18 | $18\choose{34}$ | 2.203.961.430 |
| 19 | $19\choose{34}$ | 1.855.967.520 |
| 20 | $20\choose{34}$ | 1.391.975.640 |
| 21 | $21\choose{34}$ | 927.983.760 |
| 22 | $22\choose{34}$ | 548.354.040 |
| 23 | $23\choose{34}$ | 286.097.760 |
| 24 | $24\choose{34}$ | 131.128.140 |
| 25 | $25\choose{34}$ | 52.451.256 |
| 26 | $26\choose{34}$ | 18.156.204 |
| 27 | $27\choose{34}$ | 5.379.616 |
| 28 | $28\choose{34}$ | 1.344.904 |
| 29 | $29\choose{34}$ | 278.256 |
| 30 | $30\choose{34}$ | 46.376 |
| 31 | $31\choose{34}$ | 5.984 |
| 32 | $32\choose{34}$ | 561 |
| 33 | $33\choose{34}$ | 34 |
| 34 | $34\choose{34}$ | 1 |
Die Summe aller Binomial-Koeffizienten ergibt natürlich wieder $2^{34}=17.179.869.184$ Möglichkeiten, von denen die bei der Teilsumme rot markierten einen Anteil von $1.971.226.893 = 11,47\text{ Prozent}$ ausmachen. Bei der Restsumme ist der rot markierte Anteil $1.971.226.892 = 11,47\text{ Prozent}$, also bis auf eine Möglichkeit genauso groß. Durch Ausschluss der roten Bereiche bei der Suche kann man also etwas sparen. Aber durchschlagend ist die Reduktion nicht.
Deshalb noch einmal zurück zur fehlenden unteren Schranke bei der Restsumme. Es fällt auf, dass die beiden größten Summanden weder einzeln noch zusammen in der Restsumme enthalten sein können. Damit sind sie automatisch in der Teilsumme enthalten. Das ist eine sehr wichtige Erkenntnis, die das Problem deutlich einschränkt. Aus den 34 Summanden mit der Möglichkeit, entweder in der Teilsumme enthalten zu sein oder nicht, ergibt sich damit ein reduziertes Problem mit 32 Summanden, denn für die beiden größten ist die Entscheidung schon gefallen: sie sind in der Teilsumme enthalten. Damit reduziert sich die Suche auf nur noch $2^{32} = 4.294.967.296$ Möglichkeiten. Das ist eine Ersparnis gegenüber dem ursprünglichen Problem von 75%.
Wenn also kein weiterer einfacher Weg zu einer Reduzierung der Möglichkeiten führt so sollte durch geschickte Methoden die Verkleinerung des Rechenaufwands für das Durchtesten aller Möglichkeiten vorangetrieben werden, sodass wesentlich mehr als 1000 Überprüfungen pro Sekunde erreicht werden.
Die einfache Art der Programmierung zum Finden von passenden Summanden sieht so aus: man durchläuft alle $2^{32}$ Möglichkeiten indem man jeweils die Summe der beteiligten Summanden addiert und überprüft, ob diese mit der vorgegebenen Teilsumme übereinstimmt. In VBA oder in PHP programmiert, sieht das jeweils so aus:
| VBA (EXCEL) | PHP |
|---|---|
liste(0) = 4207838
. . . . . .
liste(31) = 1722191
vorgabe = 190096861-66494921-30361805
n = 32
For i = 1 To 2 ^ n
testbit = 1
teilsumme = 0
For j = 0 To n - 1
If i And testbit > 0 Then
teilsumme = teilsumme + liste(j)
End If
testbit = testbit * 2
Next j
If teilsumme = vorgabe Then LÖSUNG
Next i
|
$liste[0] = 4207838;
. . . . . .
$liste[31] = 1722191;
$vorgabe = 190096861-66494921-30361805;
$n = 32;
For ($i = 1; $i < 1<<$n; $i++){
$testbit = 1;
$teilsumme = 0;
For ($j = 0; $j < $n; $j++){
If ($i & $testbit > 0){
teilsumme += $liste[j];
}
$testbit = $testbit << 1;
}
If ($teilsumme == $vorgabe) { LÖSUNG }
}
|
Wichtig für eine schnelle Abarbeitung sind folgende Punkte:
-
Möglichst keine Interpreter sondern Compiler benutzen.
Noch besser sind Programme, die in Assembler geschrieben werden. Das ermöglicht vollkommene Kontrolle über den Maschinencode. Praktisch reicht aber meistens das Ergebnis des Compilers. VBA (Visual Basic for Applications) innerhalb von EXCEL ist ein System mit Vorcompiler, der einen Zwischencode anlegt, diesen dann aber interpretiert. Das führt zu recht schneller Programmausführung, ist aber mit einem echten Compiler nicht vergleichbar.
Bei PHP gibt es Unterschiede. Auf HTML-Ebene (Webseiten) ist es bisher überwiegen ein Interpreter. Das hängt aber vom Provider des Servers ab. Um die Belastung des Servers durch wiederholtes Interpretieren zu mindern, arbeitet man bei neueren Versionen mit einem Bytecode-Cache. Das ist auch ein Zwischencode.
Ein wirklich schneller Compiler ist in der freien Software PureBasic enthalten, aber für diesen Fall ist darauf zu achten, dass die 64-Bit Version installiert wird. Das geht leider nur auf Rechnern mit 64 Bit CPUs. Für Rechner, die nur mit 32 Bit arbeiten, muss das Programm umgeschrieben werden (siehe weiter unten).
Mehrere Rechnerkerne (Core) sind nur dann von Vorteil, wenn man die Arbeit aufteilt, in diesem Beispiel den Gesamtumfang der Möglichkeiten in z.B. vier Teilbereiche zerlegen, für jeden Kern ein anderer Wertebereich für i. Das geht in diesem Fall recht gut, weil keine Abhängigkeiten voneinander bestehen. Leider gibt es bisher nur wenige Programmpakete, die eine solche Aufteilung automatisch vornehmen oder wenigsten innerhalb der Befehlsstruktur dem Programmierer die Möglichkeiten geben, solche Aufteilungen vorzugeben. -
Nur mit ganzen Zahlen arbeiten und die Variablen entsprechend definieren.
Für i (der Durchlauf aller Möglichkeiten) und testbit (die abzufragende Binärstelle von i) ist eine 64-Bit Zahl nötig. Für liste(), teilsumme und vorgabe reicht eine 32-Bit Zahl (ca. ± 2 Mrd.). Darin sind die mit 100 multiplizierten Euro-Beträge gespeichert. Noch weniger benötigt j, weil nur Zahlen von 0 bis 32 durchlaufen werden. Bei den meisten heutigen Rechnern sind aber keine Geschwindigkeitssteigerungen zu erreichen, wenn hier mit 8-Bit Zahlen gerechnet wird. -
Möglichst keine Multiplikationen oder Division bei ganzen Zahlen mit Potenzen von 2 durchführen.
Viele Programmiersprachen haben dafür die "shift"-Operanden wie z.B. << und >>. Dahinter muss dann noch die Anzahl der Stellenverschiebung angegeben werden. -
Die Schleife mit den häufigsten Durchläufen nicht unnötig mit Anweisungen beladen.
Im obigen Fall ist das die Schleife For j = 0 To n - 1 ... Next j. Diese wird 32 mal häufiger durchlaufen als die Schleife For i = 1 To 2 ^ n ... Next i. Aufrufe von Unterprogrammen in solchen Schleifen sind immer durch den Code des Unterprogramms zu ersetzen, um das Springen zwischen Programm und Unterprogramm zu vermeiden.
Hier ist z.B. der Gray-Code für n=4 gelistet:
| laufende Nummer | Gray-Code | ||
|---|---|---|---|
| dezimal | binär | binär | dezimal |
| 0 | 0000 | 0000 | 0 |
| 1 | 0001 | 0001 | 1 |
| 2 | 0010 | 0011 | 3 |
| 3 | 0011 | 0010 | 2 |
| 4 | 0100 | 0110 | 6 |
| 5 | 0101 | 0111 | 7 |
| 6 | 0110 | 0101 | 5 |
| 7 | 0111 | 0100 | 4 |
| 8 | 1000 | 1100 | 12 |
| 9 | 1001 | 1101 | 13 |
| 10 | 1010 | 1111 | 15 |
| 11 | 1011 | 1110 | 14 |
| 12 | 1100 | 1010 | 10 |
| 13 | 1101 | 1011 | 11 |
| 14 | 1110 | 1001 | 9 |
| 15 | 1111 | 1000 | 8 |
Wie stellt man also den Gray-Code her? Glücklicherweise ist das sehr einfach. Man nimmt die normale Zahl, die in i hochgezählt wird, bildet daraus die ganzzahlige Hälfte und verknüpft diese mit der ursprünglichen Zahl über eine Exklusiv-Oder-Funktion. Diese Bitmanipulationen sind für den Rechner kein nennenswerter Aufwand, da er sowieso im Binärcode rechnet. In den folgenden Beispielen sind die Zahlen im Binärformat dargestellt und man kann die Operationen an den Bits gut verfolgen.
| Beispiel 1 | Beispiel 2 | Beispiel 3 | |
|---|---|---|---|
| Binärzahl | 1011 | 0011011001000000111 | 001110100011010111000111 |
| Binärzahl / 2 | 0101 | 0001101100100000011 | 000111010001101011100011 |
| Gray-Code | 1110 | 0010110101100000100 | 001001110010111100100100 |
Die Umrechnung von Gray-Code in normalen Binärcode ist ungleich aufwendiger, wird aber in diesem Zusammenhang nicht gebraucht.
Beim fortschreitenden Gray-Code wird also immer nur ein Bit verändert und das entspricht dem Summanden, der zur bis dahin gebildeten Teilsumme hinzugefügt oder abgezogen werden muss. Also ist noch zu klären, welches Bit sich verändert hat, und ob dieses von 0 nach 1 oder von 1 nach 0 wechselte. Auch das sind äußerst einfache Bit-Operationen. Die Änderung findet man heraus indem man den Vorgänger Gray-Code und den neuen mit der Exklusiv-Oder-Funktion verknüpft. Das Ergebnis ist eine Zahl mit nur einem auf 1 gesetzten Bit, welches in der j-Schleife mit testbit abgefragt werden kann. Anders als in der Programmversion ohne Gray-Code wird j nicht oft zu höheren Zahlen aufsteigen müssen, weil der Gray-Code die Veränderungen überwiegen in den niederwertigen Bits vollführt. Deshalb kann die j-Schleife nach Fund des gesuchten Bits abgebrochen werden. Es gib ja kein weiteres. Durchschnittlich zählt j unabhängig von der Bitlänge dann höchstens noch bis $${\textstyle\sum\limits_{n=1}^\infty}\displaystyle\frac n{2^n}=2$$.
Zuletzt noch die Frage: addieren oder subtrahieren? Das ist ebenfalls sehr einfach zu entscheiden. Da sich nur ein Bit ändert sind all übrigen gleich. Ein Größenvergleich zwischen Vorgänger und neuem Gray-Code kann diese Entscheidung treffen. Der Mehraufwand zahlt sich trotzdem durch sehr viel schnelleres Abarbeiten in der j-Schleife aus. Es ist eine Geschwindigkeitssteigerung von bis zum 5-fachen erreichbar. Das erweiterte Kern-Programm sieht dann etwa so aus:
| VBA (EXCEL) | PHP |
|---|---|
n = 32
gray_neu = 0
teilsumme = 0
For i = 1 To 2 ^ n
gray_alt = gray_neu
gray_neu = i Xor Int(i / 2)
aktuell = gray_alt Xor gray_neu
testbit = 1
For j = 0 To n - 1
If aktuell = testbit Then
If gray_alt < gray_neu Then
teilsumme = teilsumme + liste(j)
Else
teilsumme = teilsumme - liste(j)
End If
Exit For
End If
testbit = testbit * 2
Next j
If teilsumme = vorgabe Then LÖSUNG
Next i
|
$n = 32;
$gray_neu = 0;
$teilsumme = 0;
For ($i = 1; $i < 1<<$n; $i++){
$gray_alt = $gray_neu;
$gray_neu = $i ^ ($i>>1);
$aktuell = $gray_alt ^ $gray_neu;
$testbit = 1;
For ($j = 0; $j < $n; $j++){
If ($aktuell == $testbit){
if($gray_alt < $gray_neu) {
teilsumme += $liste[$j];
}else{
$teilsumme -= $liste[$j];
}
break;
}
$testbit = $testbit << 1
}
If ($teilsumme == $vorgabe) { LÖSUNG }
}
|
Wenn man die Abarbeitungsgeschwindigkeiten gleicher Programmstrukturen auf unterschiedlichen Compilern oder Interpretern vergleicht, kommt man in etwa zu
PureBasic : VBA(EXCEL) : PHP5 = 9 : 3 : 1
Mit PureBasic ist eine Geschwindigkeit von rund 20 Mill. Prüfungen pro Sekunde erreichbar (Rechner: 64Bit 3,2GHz). Das ist gegenüber der ersten Annahme 20000 mal besser. Deshalb ist auch die Suche schon nach etwa 3,5 Minuten abgeschlossen. Das Ergebnis zeigt ein von mir erzeugtes PureBasic-Programm:
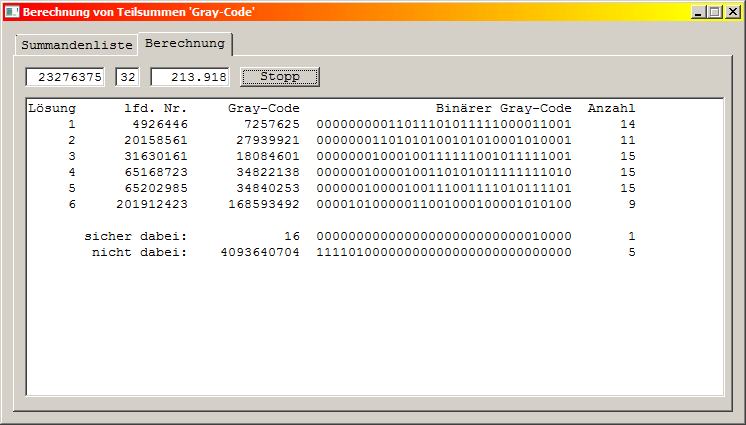
Es gibt also für dieses Rätsel nicht nur eine Summandenkombination !!
In den Feldern der oberen Zeile ist angegeben:
Restsumme (ganzzahlig): 23276375, Anzahl der Summanden: 32, Laufzeit des Programms 213,918 Sekunden.
Im Feld darunter sind die Lösungen aufgelistet. Die bei jeder Lösung angegebene laufende Nummer ist der Zählerstand (zwischen 1 und 232) zum Zeitpunkt der Lösung. Der daraus abgeleitete Gray-Code ist dezimal und binär daneben zu finden. Am Ende jeder Lösung ist die Anzahl der Summanden angegeben. Die Summanden sind in diesem Fall vor der Berechnung sortiert worden. Das ist für diese Programmstruktur nicht erforderlich, aber bietet einen Vergleich mit der nächsten Version von Programm, bei der die Rechenzeit nochmal stark reduziert werden kann.
Die Überlegung ist folgende: Man teilt den Bereich von 32 Bit in zwei Teile. Man beginnt mit dem höherwertigen Teil zu zählen und bildet dabei auch eine erste Teilsumme. Wenn diese den Vorgabewert nicht übersteigt, wird nach jedem Hochzählen um eins in den unteren Bereich verzweigt. Dort wird dann der gesamte Bereich hochgezählt und natürlich jedes Mal getestet, ob die Vorgabe genau erreicht ist. Wenn der beschriebene Vorgang sich immer so abspielen würde, hätte man keinen großen Gewinn von der Sache. Nur der Vorteil, das man die erste Teilsumme als Start für das zweite Weiterzählen nicht immer wieder neu bilden müsste. Das hatten wir aber beim Gray-Code noch besser. Der große Gewinn entsteht dadurch, dass irgendwann die Verzweigung nicht mehr in den unteren Teil erfolgt, weil die erste Teilsumme schon größer ist als die Vorgabe. Damit das möglichst optimal funktioniert, ist es erforderlich, dass die Summanden sortiert sind. Wohin legt man nun die Grenze zwischen dem höherwertigen und dem niederwertigen Bereich? Diese Bitgrenze legt man zum Testen in die Mitte, also bei 16. Der Erfolg mit dieser Technik ist durchschlagend. Statt 3,5 Minuten benötigt das Programm nur noch 16 Sekunden. Bei so kurzen Zeiten testet man auch andere Bitgrenzen und es zeigt sich dass 9 für diese Aufgabe optimal ist. Das folgende Bild zeigt den erfolgreichen Lauf mit etwa 4,5 Sekunden. Neben dem Vorteil kurzen Berechnungszeit ist auch keine 64-Bit Recheneinheit mehr erforderlich.
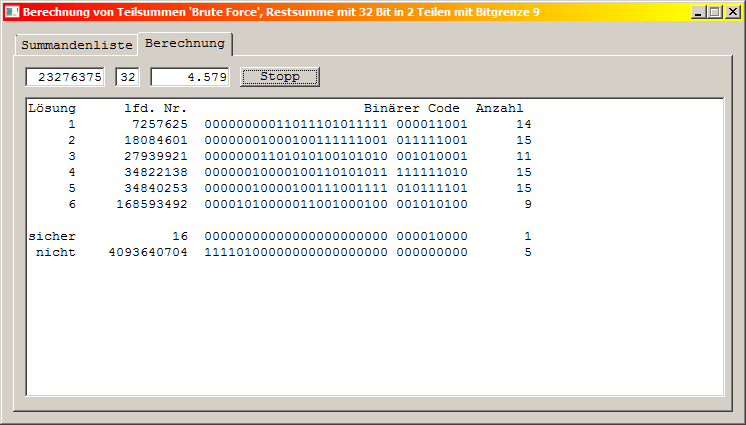
Hiermit ist die Programmoptimierung abgeschlossen.
Die so errechneten Lösungen lassen sich nach Einfügen der beiden sicheren Summanden 16 und 24 auch so darstellen:
| Nr. | alle Summanden | Summanden der Lösung Nr. | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1 | 4207838 | 4207838 | 4207838 | 4207838 | 4207838 | 0 | 4207838 |
| 2 | 1007503 | 0 | 1007503 | 0 | 0 | 1007503 | 1007503 |
| 3 | 666742 | 0 | 0 | 0 | 666742 | 666742 | 0 |
| 4 | 778520 | 778520 | 0 | 778520 | 0 | 0 | 0 |
| 5 | 5312177 | 5312177 | 0 | 5312177 | 5312177 | 0 | 5312177 |
| 6 | 631444 | 631444 | 631444 | 0 | 0 | 631444 | 631444 |
| 7 | 16845178 | 16845178 | 16845178 | 16845178 | 16845178 | 16845178 | 16845178 |
| 8 | 7727502 | 7727502 | 7727502 | 7727502 | 0 | 7727502 | 7727502 |
| 9 | 6187501 | 6187501 | 6187501 | 0 | 0 | 6187501 | 0 |
| 10 | 676742 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 778522 | 778522 | 0 | 0 | 778522 | 778522 | 0 |
| 12 | 6650892 | 6650892 | 6650892 | 6650892 | 6650892 | 6650892 | 6650892 |
| 13 | 2190734 | 0 | 2190734 | 2190734 | 0 | 2190734 | 2190734 |
| 14 | 747976 | 747976 | 0 | 0 | 747976 | 747976 | 0 |
| 15 | 3528135 | 3528135 | 0 | 0 | 3528135 | 3528135 | 0 |
| 16 | 30361805 | 30361805 | 30361805 | 30361805 | 30361805 | 30361805 | 30361805 |
| 17 | 997044 | 0 | 997044 | 0 | 997044 | 0 | 0 |
| 18 | 1808650 | 1808650 | 0 | 0 | 1808650 | 1808650 | 0 |
| 19 | 8824485 | 8824485 | 8824485 | 8824485 | 8824485 | 8824485 | 8824485 |
| 20 | 973913 | 0 | 0 | 0 | 973913 | 973913 | 0 |
| 21 | 1167753 | 0 | 0 | 0 | 1167753 | 0 | 0 |
| 22 | 617052 | 617052 | 617052 | 617052 | 617052 | 617052 | 0 |
| 23 | 3911100 | 0 | 3911100 | 3911100 | 3911100 | 0 | 3911100 |
| 24 | 66494921 | 66494921 | 66494921 | 66494921 | 66494921 | 66494921 | 66494921 |
| 25 | 1929452 | 0 | 0 | 0 | 1929452 | 0 | 0 |
| 26 | 929669 | 929669 | 929669 | 929669 | 929669 | 929669 | 0 |
| 27 | 1488704 | 1488704 | 0 | 1488704 | 1488704 | 0 | 0 |
| 28 | 1244091 | 0 | 0 | 1244091 | 1244091 | 1244091 | 1244091 |
| 29 | 12434802 | 12434802 | 12434802 | 12434802 | 12434802 | 12434802 | 12434802 |
| 30 | 452807 | 0 | 0 | 0 | 452807 | 0 | 452807 |
| 31 | 13741088 | 13741088 | 13741088 | 13741088 | 13741088 | 13741088 | 13741088 |
| 32 | 2354238 | 0 | 2354238 | 2354238 | 0 | 0 | 2354238 |
| 33 | 3982065 | 0 | 3982065 | 3982065 | 3982065 | 3982065 | 3982065 |
| 34 | 1722191 | 0 | 0 | 0 | 0 | 1722191 | 1722191 |
| Summe | 213373236 | 190096861 | 190096861 | 190096861 | 190096861 | 190096861 | 190096861 |
| Anzahl | 34 | 20 | 19 | 19 | 25 | 23 | 19 |
Zum Abschluss noch eine Übersicht über Laufzeiten des schnellsten Programms mit Bitgrenze. Dargestellt sind Serien von Zeitmessungen: einmal mit 34 Bit und das andere Mal mit 32 Bit (weil ja schon für zwei Summanden die Entscheidung getroffen ist), und das jeweils für unterschiedlich schnelle Rechner. Der langsame hat auch nur eine 32-Bit CPU und leistet trotzdem beachtliches. Die Funktionsverläufe zeigen nur die Lage der Messpunkte und sollen den Zusammenhang optisch unterstützen. Die durchgehende Funktion gibt es ja gar nicht weil es nur ganze Bits gibt. Der mittlere und obere Bereich der Bitgrenze zeigt für die Laufzeit keine großen Unterschiede. Die optimale Bitgrenze verschiebt sich nur leicht und ist 9 (32 Bit) und 11 (34 Bit). Der Versuch, mit einer weiteren Grenze und also 3 Bit-Bereichen zu rechnen brachte nur geringfügig bessere Zeiten: Grenze 10 und 5 bei 34 Bit ergab nur 10% Gewinn. Der Mehraufwand lohnte sich dafür aber nicht.
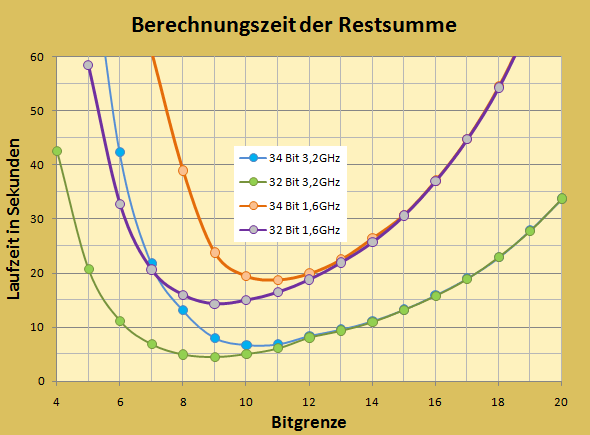
Fazit: Die am Anfang angenommene Zeit von rund 200 Tagen für das Durchtesten aller Möglichkeiten konnte schon durch sehr gute Programmiertechnik und schnelle Compiler auf unter 5 Minuten gebracht werden. Dabei hat der Gray-Code geholfen und das Reduzieren auf 32 Bit. Die zuletzt noch deutlich gesteigerte Leistung mit Bitgrenze testet zwar nicht mehr alle Möglichkeiten, aber es werden nur diejenigen ausgeschlossen, die sicher zu einer Überschreitung der vorgegebenen Summe geführt hätten. Die Reduzierung auf 32 Bit ist dabei fast unbedeutend.