Geschichten aus dem Bereich der Mathematik
1. "perfekte" Quadrate

Die Bedingung: "Zerlegung in Quadrate verschiedener Größe" ist zwar erfüllt, aber beim genauen Hinsehen ist die Ausgangsfläche kein Quadrat sondern ein Rechteck: 32 x 33. Trotzdem war die Zerlegung des obigen Rechtecks die erste dieser Art und wurde 1925 von Morón gefunden. Solche Rechtecke nennt man "perfekt".
Lange Zeit bestand wenig Hoffnung, ein "perfektes" Quadrat zu finden. Doch 1962 bewies A.J.W. Duijvestijn, dass es mindestens 21 Teilquadrate sein müssen, ohne aber eine Lösung anzugeben.
Es dauerte noch bis März 1978, als A.J.W. Duijvestijn die Zerlegung eines Quadrats in 21 verschiedene Quadrate gefunden hatte und gleichzeitig bewies, dass diese Zerlegung die einzig mögliche mit dieser Anzahl ist (abgesehen von Drehungen und Spiegelungen):
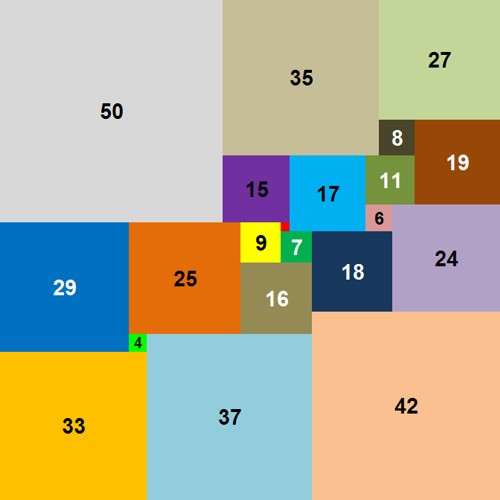
Zwischenzeitlich gab es aber eine Reihe anderer Lösungen mit mehr als 21 Teilquadraten z.B. im Jahre 1939 fand R. Sprague eine Zerlegung in 55 und 1948 Willcocks eine Zerlegung in 24 Quadrate.
Ein großer Durchbruch in der Zerlegungsmathematik wurde um 1936 von William T. Tutte und seinen Kollegen C. A. B. Smith, H. Stone und R. L. Brooks am Trinity College in Cambridge erziehlt, als er entdeckte, dass sich das Problem mit einem anderen aus der Elektrotechnik verbinden ließ. Dabei steht jedes Quadrat für einen Wiederstand konstanter Größe in einem Netzwerk, für die die Mathematik bekannt war: die Kirchhoffschen Regeln.
Diese Erkenntnis beflügelte beide Teilgebiete der Mathematik und brachte den erhofften Durchbruch. Heute ist zudem mit Computerunterstützung folgendes bekannt:
| "perfekte" Rechtecke | ||||||||
|---|---|---|---|---|---|---|---|---|
| Anzahl der Teilquadrate | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ... |
| Anzahl der Möglichkeiten | 2 | 6 | 22 | 67 | 213 | 744 | 2609 | ... |
| "perfekte" Quadrate | ||||||||
|---|---|---|---|---|---|---|---|---|
| Anzahl der Teilquadrate | 21 | 22 | 23 | 24 | 25 | 26 | 27 | ... |
| Anzahl der Möglichkeiten | 1 | 8 | 12 | 26 | 160 | 441 | 1152 | ... |
Diese Informationen wurden zusammengestellt von