Preisrätsel Januar 2009

Licht und Schatten

Zum internationalen Jahr der Astronomie startet das Preisrätsel mit einer astronomischen Frage, die auf jedes Planetensystem angewendet werden kann.
Jeder Körper in unserem Sonnensystem hat eine sonnenbeschienene Seite und eine andere, die im dunkeln liegt. Bestes und vertrautes Beispiel ist der Mond, dessen beleuchtete und dunkle Seite im Monatsrhythmus abwechselnd zu uns zeigt. Neben diesen hellen und dunklen Bereichen gibt es einen "Halbschattenring", bei dem die Sonne zwar schon die Oberfläche bescheint, aber auch zum Teil durch den Horizont verdeckt ist.
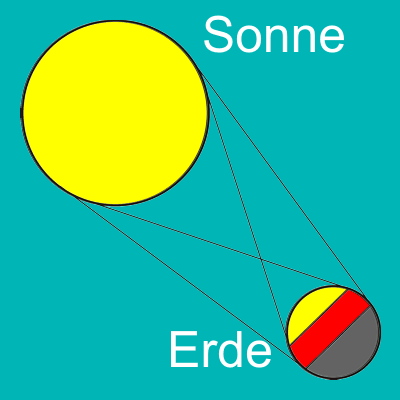
Im nebenstehenden Bild ist dies verdeutlicht: Die gelbe Kugelkappe liegt in vollem Sonnenschein, die graue voll im Nachtschatten. Die Beobachter in der roten Zone sehen die Sonne nur zum Teil am Horizont stehen. Das Bild gibt nicht die richtigen Abmessungsverhältnisse von Sonne, Erde, und dem Abstand wider, aber bei der gezeigten Konstellation ist die rote Zone maßstäblich richtig eingezeichnet, begrenzt durch die Berührpunkte der Hilfslinien.
Wenn man vereinfachend davon aus geht, das sowohl Sonne als auch Erde ideale Kugeln sind, keine Atmosphäre und Gravitationseffekte den gradlinigen Gang des Lichtes stört, ist mit ein paar Angaben die Rätselfrage zu beantworten. Suchen Sie sich die passenden Werte aus der folgenden Tabelle aus.

Abstand Mittelpunkt Erde zu Mittelpunkt Sonne = dES = 149.600.000 Kilometer

Abstand Mittelpunkt Mond zu Mittelpunkt Erde = dME = 384.400 Kilometer

Radius der Sonne = rS = 696.300 Kilometer

Radius der Erde = rE = 6.378 Kilometer

Radius des Mondes = rM = 1.738 Kilometer

 Rätselfrage: 

Wieviel Prozent der Erdoberfläche liegt im Bereich des Halbschattens?

Wer aus reinem Interesse noch etwas mehr tun will der kann nach dem gleichen Prinzip auch noch die folgenden Fragen mit den weiteren Angaben aus obiger Tabelle beantworten.

 Ergänzungsfragen: 

Die Lösung können Sie hier abschicken.

Viel Spaß bei der Suche nach der Lösung.