Lösungsbeschreibung des Preisrätsels vom Oktober 2015

1.) die Teilkörper


Aus Symmetriegründen sind diejenigen Volumina von gleicher Größe, die aus der gleichen Anzahl von Farbkugeln als Schnittmenge hervorgehen. Das sind folgende vier Gruppen:

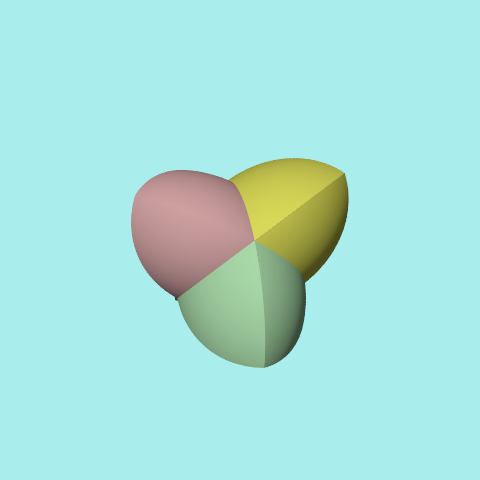4 Teile aus einer Farbe (gelbe Kugel transparent)	6 Teile aus zwei Farben (3 im Hintergrund)	4 Teile aus drei Farben (eins im Hintergrund)	1 Teil aus vier Farben ein Reuleaux-Tetraeder

2.) Vorgehensweise

Komplexe Volumina werden meist mit Integralen berechnet. Ich habe schon früher oft auf einen zweiten Lösungsweg über die numerische Integration hingewiesen. Das ist mit den heutigen PCs schneller und einfacher zu bewältigen. Da die Rechengeschwindigkeit und -genauigkeit sehr hoch ist, ist auch in vertretbarer Zeit eine ausreichend hohe Endgenauigkeit zu erreichen. In diesem Fall bietet sich dieses Verfahren besonders an, weil hier eine Behandlung mit Integralen sehr mühselig wäre.

Zur Vereinfachung setze ich den Radius der Kugeln und den Abstand der Mittelpunkte gleich 1.

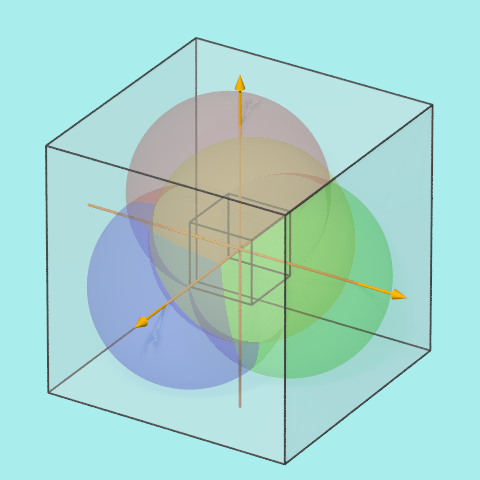
Man legt zunächst die vier Kugelmittelpunkte in die Ecken eines kleinen Würfels mit der Kantenlänge $\sqrt{2}/2$, sodass alle Abstände den Wert $1$ haben. Das ist die Länge einer Diagonalen einer Würfelseite. Man nehme sodann einen Würfel von geeigneter Größe, sodass der gesamte Körper genau hinein passt. Das ist der Fall, wenn die Kantenlänge $\sqrt{2}/2+2$ wird.

Nun teilt man den großen Würfel in sehr viele Elementarwürfel auf, z.B. in 20000*20000*20000, und prüft für jeden, ob er Anteile der vier Kugeln enthält. Das folgende BASIC-Programm führt das in erträglicher Zeit, je nach Rechner in einigen Stunden, aus:


schritte.i = 20000      // Anzahl der Schritte in jeder Dimension

Dim volumen.q(16)       // Speicher zum Zählen der Treffer
For a.i = 0 To 15       // getrennt für jede Farbkombination
    volumen(a) = 0
Next a

m.d = Sqr(2) / 4        // halbe Kantenlänge des kleinen Würfels
g.d = m + 1             // halbe Kantenlänge des großen Würfels
e.d = 2 * g / schritte  // Kantenlänge eines elementaren Würfels

x1.d = -m               // Koordinaten des Mittelpunktes der 1. Kugel
y1.d = m
z1.d = m

x2.d = m                // Koordinaten des Mittelpunktes der 2. Kugel
y2.d = -m
z2.d = m

x3.d = -m               // Koordinaten des Mittelpunktes der 3. Kugel
y3.d = -m
z3.d = -m

x4.d = m                // Koordinaten des Mittelpunktes der 4. Kugel
y4.d = m
z4.d = -m

For xAchse.i = 0 To schritte-1          // durchläuft x-Achse
    i.d = -g + e/2 + xAchse * e         // von -g+e/2 bis g-e/2
                                        // mit der Anzahl von Schritten
    xx1.d = (x1 - i) * (x1 - i)
    xx2.d = (x2 - i) * (x2 - i)
    xx3.d = (x3 - i) * (x3 - i)
    xx4.d = (x4 - i) * (x4 - i)

    For yAchse.i = 0 To schritte-1      // durchläuft y-Achse
        j.d = -g + e/2 + yAchse * e     // von -g+e/2 bis g-e/2
                                        // mit der Anzahl von Schritten
        yy1.d = (y1 - j) * (y1 - j)
        yy2.d = (y2 - j) * (y2 - j)
        yy3.d = (y3 - j) * (y3 - j)
        yy4.d = (y4 - j) * (y4 - j)

        For zAchse.i = 0 To schritte-1  // durchläuft z-Achse
            k.d = -g + e/2 + zAchse * e // von -g+e/2 bis g-e/2
                                        // mit der Anzahl von Schritten
            part.i = 0
            If xx1 + yy1 + (z1 - k) * (z1 - k) < 1
                part = part + 1
            EndIf
            If xx2 + yy2 + (z2 - k) * (z2 - k) < 1
                part = part + 2
            EndIf
            If xx3 + yy3 + (z3 - k) * (z3 - k) < 1
                part = part + 4
                EndIf
            If xx4 + yy4 + (z4 - k) * (z4 - k) < 1
                part = part + 8
            EndIf
            volumen(part) = volumen(part) + 1

        Next zAchse
    Next yAchse
Next xAchse

3.) die Rätsel-Lösung

Das Ergebnis sind 16 Zahlen im Volumen-Speicher, geordnet nach Farbanteilen. Daraus lassen sich die gewünschten Prozentwerte für jedes Volumenelement berechnen: $$Volumenprozent_n=\frac{100\cdot Volumenspeicher_n}{Summe-Volumenspeicher_0}$$ Auch eine absolute Angabe der Volumina ist möglich: $$Volumen_n/r^3=\frac{Volumenspeicher_n\cdot8\cdot(\sqrt{2}/4+1)^3}{Summe}$$

Nr	Farbtreffer	Volumenspeicher	Volumen %	Volumen/r³
0		3497177921044
1		748081303802	16,6136101	1,8551327
2		748081303802	16,6136101	1,8551327
3		156256757850	3,4701961	0,3874940
4		748081303802	16,6136101	1,8551327
5		156256757850	3,4701961	0,3874940
6		156256757850	3,4701961	0,3874940
7		100680358371	2,2359391	0,2496726
8		748081303802	16,6136101	1,8551327
9		156256757850	3,4701961	0,3874940
10		156256757850	3,4701961	0,3874940
11		100680358371	2,2359391	0,2496726
12		156256757850	3,4701961	0,3874940
13		100680358371	2,2359391	0,2496726
14		100680358371	2,2359391	0,2496726
15		170234883164	3,7806265	0,4221577
	Summe	8000000000000	100,0000000	11,1663429


Kurzbewertung dieser Information:
sehr gut	gut	befriedigend
ausreichend	mangelhaft	ungenügend