1.) Vorgehensweise
Es gibt wie sooft in der Mathematik verschiedene Möglichkeiten, um das Problem zu lösen. Hier die erste:Der Körper aus sich durchdringenden Rohren hat sehr viele Symmetrie-Ebenen und kann deshalb in viele gleichartige kleinere Elemente zerlegt werden. Zunächst reicht es, wenn man sich nur ein Rohr ansieht, z.B. das rote, und da es in einen gleichartigen oberen und einen unteren Teil infolge der Durchdringung zerteilt wurde, reicht es aus, nur die untere Hälfte zu betrachten. Diese hat weitere Symmetrien und kann in 8 volumengleiche Teile zerlegt werden:

|
= 6 x |

|
= 48 x |
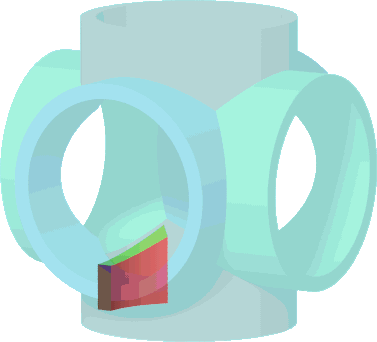
|
| gesuchtes Volumen | = 6 x | unterer roter Teilkörper | = 48 x | 1/8 des unteren Teilkörpers |
|---|
Sicherlich kann man mit viel Überlegung das Volumen des kleinen roten Teils bestimmen, aber bei der oberen Schräge muss man schon sehr aufpassen, um keine Denkfehler zu machen. Etwas einfacher scheint mir der zweite Weg zur Lösung zu sein:
Man betrachtet zunächst nicht die Rohre sondern volle Zylinder, die sich durchdringen. Anschließend subtrahiert man einen sehr ähnlichen Vollkörper mit einem kleineren Durchmesser der Zylinder:

|
= |
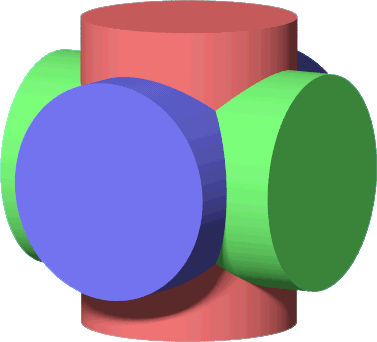
|
- |
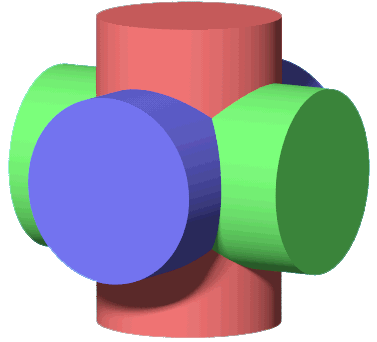
|
| gesuchtes Volumen | = | großer Vollkörper | - | kleiner Vollkörper |
|---|
Wenn man sich senkrechte Schnitte durch die Vollkörper ansieht, sind je nach Schnittposition drei unterschiedliche Fälle zu unterscheiden:

|

|

|
| Fall I | Fall II | Fall III |
|---|
Im ersten Fall hat die graue Schnittfläche eine Kreuzform, die zwar mit Verschiebung der Schnittebene variiert, aber sehr leicht zu berechnen ist.
Der zweite Fall ist deutlich komplizierter, aber doch sehr übersichtlich zu lösen. Dazu folgt weiter unten eine Zeichnung, mit der das Problem angegangen werden kann.
Der dritte Fall ist der einfachste. Die Schnittebene ist eine konstante Kreisfläche.
2.) Definitionen und Zusammenhänge
Die für diese Aufgabe benutzten Größen sind: $$h=\text{Länge oder Höhe eines Zylinders} \\ r=\text{Radius oder halber Durchmesser eines Zylinders}$$ Die Größen der verschiedenen Schnittfächen sind eine Funktion der Schnittposition, die von der Mitte des blauen Zylinders entlang seiner Rotationsachse bis zu seinem Ende gezählt werden soll. Diese Achse nenne ich die x-Achse, über die die Schnittscheiben aufsummiert werden können (Integration). Als Ergebnis erhält man das halbe Volumen des großen bzw. kleinen Vollkörpers, je nach dem, welchen Radius man für die Zylinder wählt, den äußeren oder den inneren. Die Längen sind in beiden Körpern gleich, und somit auch der zu integrierende Bereich. Die Intervalle innerhalb des Bereichs werden aber unterschiedlich ausfallen.Wo liegen diese Intervallgrenzen? Dazu hilft ein Blick auf die folgende Zeichnung:
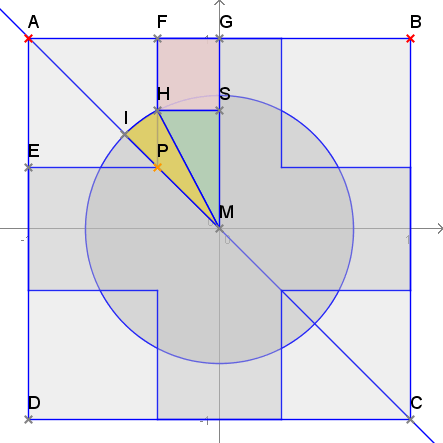
Dargestellt ist eine Schnittebene aus dem Bereich Fall II. Wegen der räumlichen Symmetrie des Körpers ist die Schnittposition auch auf dieser Projektion erkennbar als horizontale Gerade durch Punkt $S$. Hier wird klar, dass $x$ der Strecke $\overline{MS}$ entspricht. Wird $x$ größer, wandert Punkt $H$ auf $S$ zu und bei $x=r$ verschwindet der Anteil des Kreuzes und nur der Kreis bleibt. Das ist also die obere Schranke für den Fall II. Wird $x$ kleiner, so wandert $H$ auf $I$ zu und damit verschwindet der Kreisanteil. Diese unter Grenze liegt bei $x=\frac r2\cdot\sqrt{2}$.
Die Intervallgrenzen für den Fall I und III sind damit auch festgelegt, weil der gesamte $x$-Bereich von $0$ bis $\frac h2$ geht. In der folgenden Tabelle sind diese Intervalle aufgelistet.
| Fall | Form der Schnittfläche |
Intervall $x$ | Fläche $F(x)$ | |
|---|---|---|---|---|
| von | bis | |||
| I | Kreuz | $0$ | $\frac r2\cdot\sqrt{2}$ | $h^2-4\cdot (\frac h2 -\sqrt{r^2-x^2})^2$ |
| II | Kreuz und Kreis | $\frac r2\cdot\sqrt{2}$ | $r$ | $8\cdot\left( \tona{ \sqrt{r^2-x^2}\cdot(\frac h2 -x) } + \tonb{ \frac x2 \cdot\sqrt{r^2-x^2} } + \tonc{ (\frac{\pi}4 -\arccos{\frac xr})\cdot\frac{\pi r^2}{2\pi} } \right)$ |
| III | Kreis | $r$ | $\frac h2$ | $\pi r^2$ |
Aus der obigen Zeichnung lassen sich auch die Flächen in Abhängigkeit vom Fall und von $x$ erkennen.
Fall I: Das Kreuz ist ein Quadrat $□ ABCD$ reduziert um 4 Eckquadrate $□ AFPE$.
Dabei ist die Strecke $\overline{AB}=h$ und die Strecke $\overline{AF}=\frac h2 -\sqrt{r^2-x^2}$
Fall II: Ein Achtel der kombinierten Fläche aus Kreuz und Kreis lässt sich durch drei farbige Teilflächen darstellen.
Das $\tona{\text{Rechteck}}$ $□ FGSH$ hat die Seiten $\overline{FG}=\sqrt{r^2-x^2}$ und $\overline{SG}=\frac h2 -x$.
Das rechtwinklige $\tonb{\text{Dreieck}}$ $△ MSH$ hat die Katheten $\overline{MS}=x$ und $\overline{SH}=\sqrt{r^2-x^2}$
Der $\tonc{\text{Kreissektor}}$ oder Kreisausschnitt ist bestimmt durch den Radius $r$ und den Mittelpunktswinkel $\frac{\pi}4 -\arccos{\frac xr}$.
Fall III: Die Kreisfläche hat die konstante Größe von $\pi r^2$.
3.) Berechnung mit Integralen
Nun kann man alles zusammenfassen. Das Volumen eines Vollkörpers ist: $$\sand{V=2\cdot\left(\intop_0^{\frac r2\cdot\sqrt{2}}F_{I}(x)dx+\intop_{\frac r2\cdot\sqrt{2}}^r F_{II}(x)dx+\intop_r^{\frac h2}F_{III}(x)dx\right)}$$ Für das Lösen solcher Integrale kann man auf Formelsammlungen zurückgreifen aber einfacher ist, den Computer, der mit dem Internet verbunden ist, selbst zum Berechnen heranzuziehen. Es bieten sich einige Internetseiten zur kostenlosen Nutzung dafür an:matheguru.com oder Integralrechner oder wolframAlpha Integralrechner
| Fall I: | $$\sand{V_I=\intop_0^{\frac r2\cdot\sqrt{2}}F_{I}(x)dx=\intop_0^{\frac r2\cdot\sqrt{2}}h^2-4\cdot \left(\frac h2 -\sqrt{r^2-x^2}\right)^2dx }$$ zuerst Klammer auflösen und vereinfachen dann einfache Anteile des Integrals ausrechnen $$\sand{V_I=4\cdot\intop_0^{\frac r2\cdot\sqrt{2}}\left(h\cdot\sqrt{r^2-x^2}-r^2+x^2\right)\;dx=4h\cdot\intop_0^{\frac r2\cdot\sqrt{2}}\sqrt{r^2-x^2}\;dx-2r^3\cdot\sqrt{2}+\frac13\cdot r^3\cdot\sqrt{2}}$$ der schwierigste Teil ist nun noch das übrig gebliebene Integral: $$\sand{\intop_0^{\frac r2\cdot\sqrt{2}}\sqrt{r^2-x^2}\;dx=\left[\frac12\cdot\left({r}^2\cdot\arcsin\frac xr+x\cdot\sqrt{r^2-x^2}\right)\right]_0^{\frac r2\cdot\sqrt{2}}=(\frac{\pi}2+1)\cdot\frac{r^2}4}$$ dabei ist $\arcsin(\frac12\cdot\sqrt{2})=\frac{\pi}4$ $$\sand{V_I=\left(\frac{\pi}2+1\right)\cdot hr^2-\frac53\sqrt{2}\cdot r^3}$$ |
| Fall II: | $$\sand{V_{II}=\intop_{\frac r2\cdot\sqrt{2}}^{r}F_{II}(x)dx=8\cdot\intop_{\frac r2\cdot\sqrt{2}}^{r}\left( \tona{ \sqrt{r^2-x^2}\cdot(\frac h2 -x) } + \tonb{ \frac x2 \cdot\sqrt{r^2-x^2} } + \tonc{ (\frac{\pi}4 -\arccos{\frac xr})\cdot\frac{\pi r^2}{2\pi} } \right)dx}$$ $$\sand{V_{II}=4\cdot\intop_{\frac r2\cdot\sqrt{2}}^{r}\left(\sqrt{r^2-x^2}\cdot(h-x)+\frac{\pi r^2}4-r^2\cdot\arccos{\frac xr}\right)dx}$$ das schwierigste noch nicht bearbeitete Integral hat folgende Auflösung: $$\sand{\intop_{\frac r2\cdot\sqrt{2}}^{r}\arccos\frac xr dx=\left[x\cdot\arccos\frac xr-r\cdot\sqrt{1-\frac{x^2}{r^2}}\right]_{\frac r2\cdot\sqrt{2}}^{r}=r\cdot\sqrt{2}\cdot\left(\frac 12-\frac{\pi}8\right)}$$ wesentlich einfacher ist $$\sand{\intop_{\frac r2\cdot\sqrt{2}}^{r}x\cdot\sqrt{r^2-x^2}\;dx=\left[-\frac13\cdot(r^2-x^2)^{\frac32}\right]_{\frac r2\cdot\sqrt{2}}^{r}=\frac1{12}\sqrt{2}\cdot r^3}$$ hier nun die Zusammenfassung: $$\sand{V_{II}=\pi\cdot r^3+\frac{\pi}2\cdot hr^2-hr^2-\frac{7r^3\cdot\sqrt{2}}{3}}$$ $$\sand{V_{II}=(\pi-\frac73\cdot\sqrt{2})\cdot r^3+(\frac{\pi}2-1)\cdot hr^2}$$ |
| Fall III: | $$\sand{V_{III}=\intop_r^{\frac h2}F_{III}(x)dx=\intop_r^{\frac h2}\pi r^2 dx=(\frac h2 -r)\cdot\pi r^2}$$ |
4.) Berechnung mit EXCEL
Wenn man mal schnell einen Überblick über ein Problem benötigt, ist EXCEL das richtige Werkzeug. Auch für dieses Rätsel lag schnell ein Ergebnis vor. Natürlich müssen die gleichen Überlegungen angestellt werden, wie oben beschrieben. Aber der Weg der numerischen Integration ist wesentlich einfacher und schneller zu bewerkstelligen. Statt wie beim Integral einen Grenzwertübergang nach unendlich zu machen und oft mühsam nach der richtigen Stammfunktion zu suchen bleibt man bei endlichen Schrittzahlen und dem einfacheren funktionalen Zusammenhang. Da der Rechner sehr schnell ist sind Schrittzahlen von Millionen zur Erzielung hoher Genauigkeit kein Problem. Durch die vorangegangene Aufarbeitung sind keine weiteren Erklärungen für das Programm nötig. Die benutzten Variablen haben im Wesentlichen gleiche Namen.Hier soll noch der Hinweis erfolgen, dass nicht immer alle benötigten Funktionen in EXCEL eingebaut sind. In diesem Beispiel fehlte die Funktion "arcuscosinus". Deshalb ist unterhalb der Funktion "Vverbindung" noch die Funktion "Arccos" angefügt.
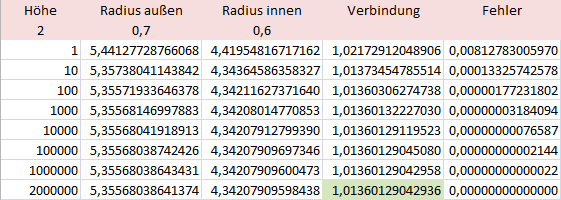
Ich benutzte die maximale Schrittzahl 2.000.000 für die numerische Integration.
Function Vvollkoerper(schritte, r, h)
Pi = 4 * Atn(1)
r2 = r * r
h2 = h * h
limit0 = 0
limit1 = r / 2 * Sqr(2)
limit2 = r
limit3 = h / 2
vI = 0: vII = 0: vIII = 0
delta = (limit1 - limit0) / schritte
For i = 1 To schritte
x = limit0 + i * delta - delta / 2
b = Sqr(r2 - x * x)
c = h / 2 - b
vI = vI + (h2 - 4 * c * c) * delta
Next i
delta = (limit2 - limit1) / schritte
For i = 1 To schritte
x = limit1 + i * delta - delta / 2
b = Sqr(r2 - x * x)
fRechteck = b * (h / 2 - x)
fDreieck = x * b / 2
fKreissektor = (Pi / 4 - Arccos(x / r)) * r2 / 2
vII = vII + 8 * (fRechteck + fDreieck + fKreissektor) * delta
Next i
vIII = (limit3 - limit2) * Pi * r2
Vvollkoerper = (vI + vII + vIII) * 2
End Function
Function Arccos(w)
Arccos = Atn(-w / Sqr(-w * w + 1)) + 2 * Atn(1)
End Function
|