Wie sooft bei mathematischen Fragestellungen gibt es unterschiedliche Wege zum Ziel.
Glücklicherweise führt die Mathematik auch bei den verschiedenen Vorgehensweisen immer zum gleichen Ergebnis.
Manchmal ist das Problem aber trotz einfacher Fragestellung sehr verzwickt
und die einfachste der Lösung hängt sehr stark von der geeigneten Wahl der Parameter ab.
Hier liegt auch ein solcher Fall vor und ich bin nicht sicher, ob es vielleicht noch einfacher geht als hier beschrieben.
Immerhin liefen alle meine Versuche immer auf eine algebraisch nicht lösbare Gleichung hinaus.
Das ist zwar unangenehm aber kommt in der Praxis häufig vor.
Dann sind geeignete Näherungsverfahren gefragt.
Vorgehensweise: Bei Rotationskörper-Berechnungen von nicht in Formelsammlungen befindlichen Volumina (Kugel, Kegel, Zylinder, Torus usw.)
bietet sich die Integralrechnung an.
Diese ist universell einsetzbar, aber liefert nicht immer einfache Strukturen und es kann leicht vorkommen, dass man den Überblick verliert.
Trotzdem ist es eine richtige Vorgehensweise, wenn es nichts Einfacheres gibt.
In diesem Fall fand ich aber einen Weg, der schon von einem Mathematiker des 16. Jahrhunderts beschritten wurde:
Paul Guldin, ursprünglich Habakuk Guldin (* 12. Juni 1577 in Mels; † 3. November 1643 in Graz), war Astronom und Professor für Mathematik in Graz und Wien.
Seine Regel lautet:
Das Volumen eines Rotationskörpers ist gleich dem Produkt aus dem Flächeninhalt der erzeugenden Fläche
und dem Umfang des Kreises, der durch die Rotation des Schwerpunktes dieser Fläche erzeugt wird.
Das hört sich einfach an, aber es bleibt die Fläche und die Lage des Schwerpunktes der Fläche zu bestimmen.
Da alle die dies lesen (wenn es nicht gerade ein Ausdruck der Internetseite ist) auch sofortigen Zugang zu mathematischen Formelsammlungen im Internet haben,
ist es einfach, die passenden Formeln zu finden.
Wenn man sich allerdings nicht auf solche Formeln stützen will, bietet sich hier an, die Integralrechnung doch noch zu bemühen.
Die hier auftretenden Flächen sind Kreissegmente, auch Kreisabschnitte genannt.
Dabei hat sich herausgestellt, dass der Mittelpunktswinkel $α$ als Parameter sowohl für die Fläche als auch für den Schwerpunkt eine geeignete Größe darstellt.
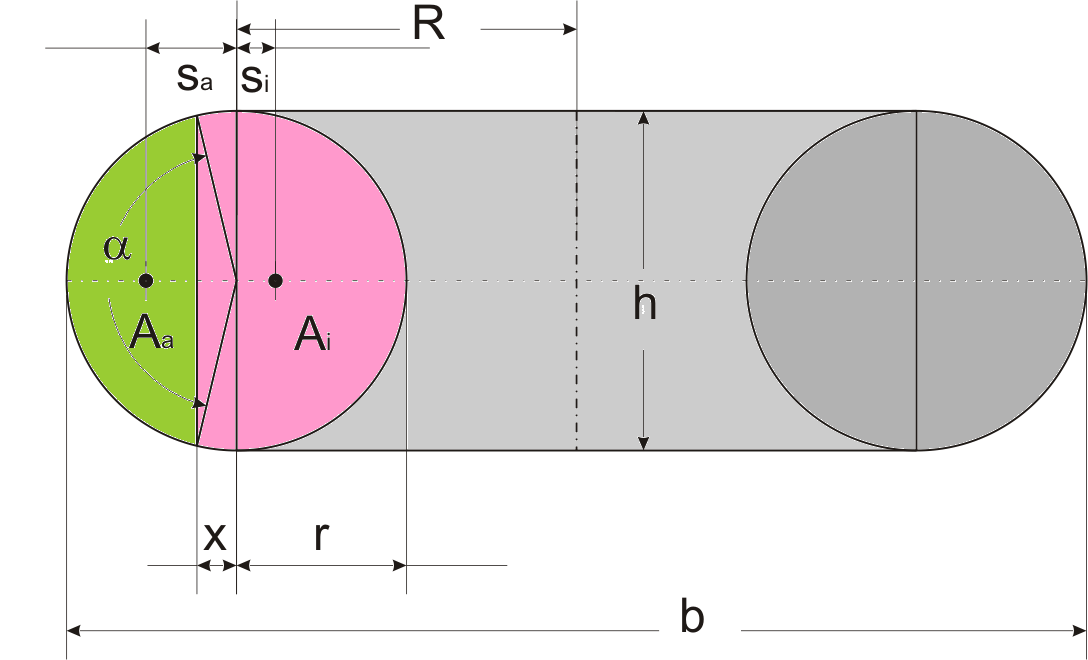
In der unten stehenden Figur ist dieser eingezeichnet, zusammen mit den im weiteren verwendeten Größen. Es ist üblich für Flächen Großbuchstaben und für Strecken Kleinbuchstaben zu verwenden.
Hier gibt es eine Ausnahme: Das große $R$ ist eine Strecke, die sich vom kleinen $r$ unterscheiden soll, ohne dass man auf weitere Indizes zurückgreifen muss.
Die ansonsten benutzten Indizes sind $a$ für außen und $i$ für innen.
Die Strecken s sind die Abstände der Schwerpunkte vom Radius $R$.