1.) Voraussetzungen
Gegeben sind die drei Seiten eines sphärischen Dreiecks:
$$
a=1 \\
b=3 \\
c=5\tag{0}
$$
Gesucht ist der Kugelradius $r$, bei dem der Flächeninhalt $A$ des Dreiecks minimal wird.
2.) der Seiten-Kosinussatz
In jedem sphärischen Dreieck gilt der Seiten-Kosinussatz:
$$
\cos \frac ar = \cos \frac br \cdot \cos \frac cr + \sin \frac br \cdot \sin\frac cr \cdot \cos \alpha \\
\cos \frac br = \cos \frac ar \cdot \cos \frac cr + \sin \frac ar \cdot \sin \frac cr \cdot \cos \beta \\
\cos \frac cr = \cos \frac ar \cdot \cos \frac br + \sin \frac ar \cdot \sin \frac br \cdot \cos \gamma\tag{1}
$$
und nach den Winkeln aufgelöst:
$$
\alpha = \arccos\left(\frac{\cos \frac ar-\cos \frac br \cdot \cos \frac cr}{\sin \frac br \cdot \sin \frac cr}\right) \\
\beta = \arccos\left(\frac{\cos \frac br-\cos \frac ar \cdot \cos \frac cr}{\sin \frac ar \cdot \sin \frac cr}\right) \\
\gamma = \arccos\left(\frac{\cos \frac cr-\cos \frac ar \cdot \cos \frac br}{\sin \frac ar \cdot \sin \frac br}\right)\tag{2}
$$
3.) die Flächenformel
Die Fläche eines sphärischen Dreiecks berechnet sich zu
$$
A=(\alpha + \beta + \gamma - \pi)\cdot r^2\tag{3}
$$
4.) der erlaubte Bereich für den Kugelradius
Wenn $r$ sehr groß ist, gibt es kein reales Kugeldreieck mit den gegebenen Abmessungen.
Der Radius muss so klein werden, dass die lange Seite $c$ mehr als die Hälfte des Umfangs ausmacht.
Der Rest des Umfangs entfällt dann auf die Seiten $a$ und $b$.
Wenn zwischen $a$ und $b$ ein Winkel von $\pi$ ist, ist der maximale Radius erreicht.
Bei einem Winkel von $0$ ist der minimale Radius der Kugel gegeben.
$$
r_{max}=\frac{c+a+b}{2\pi}=\frac9{2\pi}=1,43239449 \\
r_{min}=\frac{c-a+b}{2\pi}=\frac7{2\pi}=1,11408460$$
In beiden Fällen ist der Flächeninhalt des sphärischen Dreiecks gleich der halben Kugeloberfläche:
$$
A(r_{max})=2\pi\cdot{r_{max}}^2=12,89155039 \\
A(r_{min})=2\pi\cdot{r_{min}}^2=7,79859221$$
Die minimale Fläche muss also kleiner als $A(r_{min})$ sein und der gesuchte Radius zwischen $r_{min}$ und $r_{max}$ liegen.
 |
a = 1
b = 3
c = 5
|
5.) die Flächenfunktion A(r)
Die Funktion A(r) ergibt sich wenn in Gleichung (3) die Winkel von Gleichung (2) und die Werte von (0) eingesetzt werden.
Diese Funktion ist zu komplex, um auf analytischem Wege die Ableitung zu bilden.
Aber eine nummerische Lösung ist natürlich möglich.
Besondere Beachtung sollte auf die Berechnung der Winkel gelegt werden.
Die $\arccos$-Funktion ist mehrdeutig und der Winkel $\gamma$ ist,
anders als die beiden anderen Winkel des sphärischen Dreiecks, größer als $\pi$ oder 180°.
Deshalb muss nicht der typische eingeschränkte Definitionsbereich $[0,\pi ]$ sondern der Ergänzungswinkel zu $2\pi$ genommen werden.
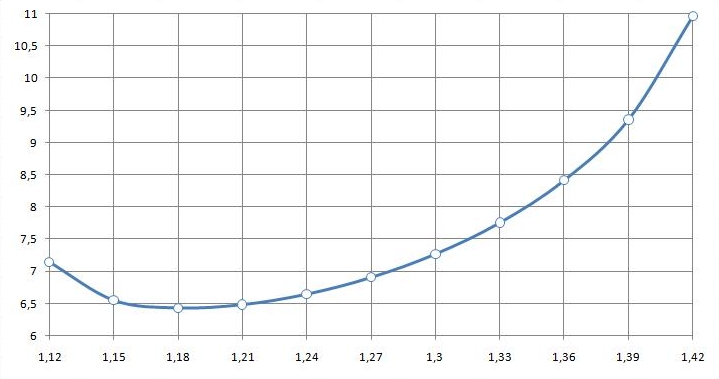
Eine Wertetabelle gibt zunächst einen guten Überblick über den Funktionsverlauf von $A(r)$:
| r | A(r) |
|---|
| 1,12 | 7,1489 |
| 1,15 | 6,5578 |
| 1,18 | 6,4400 |
| 1,21 | 6,4909 |
| 1,24 | 6,6535 |
| 1,27 | 6,9132 |
| 1,30 | 7,2746 |
| 1,33 | 7,7595 |
| 1,36 | 8,4162 |
| 1,39 | 9,3553 |
| 1,42 | 10,9565 |
|
|
Mit einer Intervallschachtelung kann man sich dem Minimum der Fläche nähern,
indem man die Radien der jeweils zwei kleinsten Flächen als Grenzen der folgenden Tabellen verwendet.
| r | A(r) |
|---|
| 1,180 | 6,440009 |
| 1,183 | 6,439020 |
| 1,186 | 6,439539 |
| 1,189 | 6,441493 |
| 1,192 | 6,444820 |
| 1,195 | 6,449465 |
| 1,198 | 6,455376 |
| 1,201 | 6,462510 |
| 1,204 | 6,470828 |
| 1,207 | 6,480294 |
| 1,210 | 6,490877 |
| r | A(r) |
|---|
| 1,1830 | 6,43902046 |
| 1,1833 | 6,43900572 |
| 1,1836 | 6,43900596 |
| 1,1839 | 6,43902113 |
| 1,1842 | 6,43905113 |
| 1,1845 | 6,43909590 |
| 1,1848 | 6,43915537 |
| 1,1851 | 6,43922946 |
| 1,1854 | 6,43931812 |
| 1,1857 | 6,43942126 |
| 1,1860 | 6,43953882 |
| r | A(r) |
|---|
| 1,18330 | 6,4390057159 |
| 1,18333 | 6,4390050675 |
| 1,18336 | 6,4390045689 |
| 1,18339 | 6,4390042200 |
| 1,18342 | 6,4390040208 |
| 1,18345 | 6,4390039711 |
| 1,18348 | 6,4390040710 |
| 1,18351 | 6,4390043203 |
| 1,18354 | 6,4390047190 |
| 1,18357 | 6,4390052669 |
| 1,18360 | 6,4390059641 |
| r | A(r) |
|---|
| 1,183420 | 6,439004020784 |
| 1,183423 | 6,439004009090 |
| 1,183426 | 6,439003998892 |
| 1,183429 | 6,439003990190 |
| 1,183432 | 6,439003982983 |
| 1,183435 | 6,439003977272 |
| 1,183438 | 6,439003973056 |
| 1,183441 | 6,439003970336 |
| 1,183444 | 6,439003969111 |
| 1,183447 | 6,439003969381 |
| 1,183450 | 6,439003971146 |
| r | A(r) |
|---|
| 1,1834440 | 6,43900396911077 |
| 1,1834443 | 6,43900396907049 |
| 1,1834446 | 6,43900396904517 |
| 1,1834449 | 6,43900396903480 |
| 1,1834452 | 6,43900396903938 |
| 1,1834455 | 6,43900396905891 |
| 1,1834458 | 6,43900396909340 |
| 1,1834461 | 6,43900396914283 |
| 1,1834464 | 6,43900396920722 |
| 1,1834467 | 6,43900396928656 |
| 1,1834470 | 6,43900396938085 |
| r | A(r) |
|---|
| 1,18344490 | 6,4390039690347972 |
| 1,18344493 | 6,4390039690345824 |
| 1,18344496 | 6,4390039690345172 |
| 1,18344499 | 6,4390039690346015 |
| 1,18344502 | 6,4390039690348353 |
| 1,18344505 | 6,4390039690352186 |
| 1,18344508 | 6,4390039690357515 |
| 1,18344511 | 6,4390039690364339 |
| 1,18344514 | 6,4390039690372657 |
| 1,18344517 | 6,4390039690382472 |
| 1,18344520 | 6,4390039690393781 |
| r | A(r) |
|---|
| 1,183444930 | 6,439003969034582419 |
| 1,183444933 | 6,439003969034569169 |
| 1,183444936 | 6,439003969034557413 |
| 1,183444939 | 6,439003969034547153 |
| 1,183444942 | 6,439003969034538388 |
| 1,183444945 | 6,439003969034531118 |
| 1,183444948 | 6,439003969034525343 |
| 1,183444951 | 6,439003969034521063 |
| 1,183444954 | 6,439003969034518279 |
| 1,183444957 | 6,439003969034516989 |
| 1,183444960 | 6,439003969034517195 |
| r | A(r) |
|---|
| 1,1834449570 | 6,43900396903451698945 |
| 1,1834449573 | 6,43900396903451694277 |
| 1,1834449576 | 6,43900396903451691103 |
| 1,1834449579 | 6,43900396903451689424 |
| 1,1834449582 | 6,43900396903451689241 |
| 1,1834449585 | 6,43900396903451690553 |
| 1,1834449588 | 6,43900396903451693360 |
| 1,1834449591 | 6,43900396903451697662 |
| 1,1834449594 | 6,43900396903451703460 |
| 1,1834449597 | 6,43900396903451710752 |
| 1,1834449600 | 6,43900396903451719540 |
| r | A(r) |
|---|
| 1,18344495790 | 6,4390039690345168942441 |
| 1,18344495793 | 6,4390039690345168933880 |
| 1,18344495796 | 6,4390039690345168926814 |
| 1,18344495799 | 6,4390039690345168921243 |
| 1,18344495802 | 6,4390039690345168917167 |
| 1,18344495805 | 6,4390039690345168914587 |
| 1,18344495808 | 6,4390039690345168913502 |
| 1,18344495811 | 6,4390039690345168913911 |
| 1,18344495814 | 6,4390039690345168915817 |
| 1,18344495817 | 6,4390039690345168919217 |
| 1,18344495820 | 6,4390039690345168924112 |
| r | A(r) |
|---|
| 1,183444958080 | 6,439003969034516891350164 |
| 1,183444958083 | 6,439003969034516891347534 |
| 1,183444958086 | 6,439003969034516891346399 |
| 1,183444958089 | 6,439003969034516891346760 |
| 1,183444958092 | 6,439003969034516891348616 |
| 1,183444958095 | 6,439003969034516891351967 |
| 1,183444958098 | 6,439003969034516891356813 |
| 1,183444958101 | 6,439003969034516891363155 |
| 1,183444958104 | 6,439003969034516891370991 |
| 1,183444958107 | 6,439003969034516891380323 |
| 1,183444958110 | 6,439003969034516891391150 |
| r | A(r) |
|---|
| 1,1834449580860 | 6,43900396903451689134639934 |
| 1,1834449580863 | 6,43900396903451689134636813 |
| 1,1834449580866 | 6,43900396903451689134635186 |
| 1,1834449580869 | 6,43900396903451689134635055 |
| 1,1834449580872 | 6,43900396903451689134636419 |
| 1,1834449580875 | 6,43900396903451689134639278 |
| 1,1834449580878 | 6,43900396903451689134643633 |
| 1,1834449580881 | 6,43900396903451689134649482 |
| 1,1834449580884 | 6,43900396903451689134656827 |
| 1,1834449580887 | 6,43900396903451689134665667 |
| 1,1834449580890 | 6,43900396903451689134676002 |
| r | A(r) |
|---|
| 1,18344495808660 | 6,4390039690345168913463518630 |
| 1,18344495808663 | 6,4390039690345168913463510589 |
| 1,18344495808666 | 6,4390039690345168913463504044 |
| 1,18344495808669 | 6,4390039690345168913463498993 |
| 1,18344495808672 | 6,4390039690345168913463495438 |
| 1,18344495808675 | 6,4390039690345168913463493378 |
| 1,18344495808678 | 6,4390039690345168913463492813 |
| 1,18344495808681 | 6,4390039690345168913463493744 |
| 1,18344495808684 | 6,4390039690345168913463496170 |
| 1,18344495808687 | 6,4390039690345168913463500090 |
| 1,18344495808690 | 6,4390039690345168913463505506 |
| r | A(r) |
|---|
| 1,183444958086750 | 6,439003969034516891346349337821 |
| 1,183444958086753 | 6,439003969034516891346349325445 |
| 1,183444958086756 | 6,439003969034516891346349314565 |
| 1,183444958086759 | 6,439003969034516891346349305180 |
| 1,183444958086762 | 6,439003969034516891346349297290 |
| 1,183444958086765 | 6,439003969034516891346349290895 |
| 1,183444958086768 | 6,439003969034516891346349285995 |
| 1,183444958086771 | 6,439003969034516891346349282591 |
| 1,183444958086774 | 6,439003969034516891346349280681 |
| 1,183444958086777 | 6,439003969034516891346349280267 |
| 1,183444958086780 | 6,439003969034516891346349281348 |
| r | A(r) |
|---|
| 1,1834449580867740 | 6,43900396903451689134634928068130 |
| 1,1834449580867743 | 6,43900396903451689134634928057260 |
| 1,1834449580867746 | 6,43900396903451689134634928047886 |
| 1,1834449580867749 | 6,43900396903451689134634928040007 |
| 1,1834449580867752 | 6,43900396903451689134634928033623 |
| 1,1834449580867755 | 6,43900396903451689134634928028734 |
| 1,1834449580867758 | 6,43900396903451689134634928025341 |
| 1,1834449580867761 | 6,43900396903451689134634928023443 |
| 1,1834449580867764 | 6,43900396903451689134634928023039 |
| 1,1834449580867767 | 6,43900396903451689134634928024132 |
| 1,1834449580867770 | 6,43900396903451689134634928026719 |
| r | A(r) |
|---|
| 1,18344495808677610 | 6,4390039690345168913463492802344256 |
| 1,18344495808677613 | 6,4390039690345168913463492802333497 |
| 1,18344495808677616 | 6,4390039690345168913463492802324233 |
| 1,18344495808677619 | 6,4390039690345168913463492802316464 |
| 1,18344495808677622 | 6,4390039690345168913463492802310190 |
| 1,18344495808677625 | 6,4390039690345168913463492802305411 |
| 1,18344495808677628 | 6,4390039690345168913463492802302128 |
| 1,18344495808677631 | 6,4390039690345168913463492802300340 |
| 1,18344495808677634 | 6,4390039690345168913463492802300047 |
| 1,18344495808677637 | 6,4390039690345168913463492802301249 |
| 1,18344495808677640 | 6,4390039690345168913463492802303946 |
| r | A(r) |
|---|
| 1,183444958086776310 | 6,439003969034516891346349280230033967 |
| 1,183444958086776313 | 6,439003969034516891346349280230024309 |
| 1,183444958086776316 | 6,439003969034516891346349280230016145 |
| 1,183444958086776319 | 6,439003969034516891346349280230009476 |
| 1,183444958086776322 | 6,439003969034516891346349280230004303 |
| 1,183444958086776325 | 6,439003969034516891346349280230000625 |
| 1,183444958086776328 | 6,439003969034516891346349280229998442 |
| 1,183444958086776331 | 6,439003969034516891346349280229997754 |
| 1,183444958086776334 | 6,439003969034516891346349280229998561 |
| 1,183444958086776337 | 6,439003969034516891346349280230000864 |
| 1,183444958086776340 | 6,439003969034516891346349280230004662 |
So findet man bei einem Radius von 1,183444958086776331 die minimale Fläche.
| Radius r | 1,183444958086776331 |
| Fläche A | 6,439003969034516891 |
| alpha | 2,157701737812460078 | 123,62720302° |
| beta | 0,687551689616370590 | 39,39381001° |
| gamma | 4,893847985184389429 | 280,39683513° |

