1.) Schwimmen, Schweben, Sinken
Ob ein Körper schwimmt, schwebt oder sinkt hängt von seinem Material und der Flüssigkeit ab.
Dabei ist die mittlere Dichte $\rho_{Substanz}$ für beide Substanzen kennzeichnend:
$$
\rho_{Substanz}=\frac{Masse [t]}{Volumen [m^3]}=\frac{Masse [kg]}{Volumen [l]}=\frac{Masse [g]}{Volumen [cm^3]}
$$
Ein Körper schwimmt, wenn folgende Bedingung erfüllt ist:
$$
0<\frac{\rho_{Körper}}{\rho_{Flüssigkeit}}<1
$$
Da hier nur das Schwimmen auf Wasser mit $\rho_{Wasser}=1\frac{g}{cm^3}$ behandelt wird, gilt für die relative Dichte $\rho$ des schwimmenden Körpers
$$
0<\rho<1
$$
Ein Körper schwebt im Wasser bei $\rho=1$ und sinkt bei $\rho>1$.
Das Material Holz ohne Hohlräume, die auch oft mit Wasser gefüllt sind, hat eine relative Dichte von 1,5.
Tatsächlich gibt es aber kein Holz ohne Hohlräume.
Auch ein Holz ohne Wasser in den Hohlräumen ist eine Seltenheit.
Daher ist der wirkliche Dichtebereich von 0,2 bis 1,1 je nach Holzart und Trocknung.
2.) die Schwimmkörper und deren Schwimmlagen
Die Form von Schwimmkörper und deren Dichte ist maßgebend für deren stabile Schwimmlagen.
Hier wird die Form eines
Zylinders gewählt.
Die Schwimmlage kann durch die
Eintauchtiefe und durch den
Winkel zwischen Symmetrieachse des Zylinders und der Senkrechten zur Wasseroberfläche vollständig beschrieben werden.
Beide Parameter hängen von der relativen
Dichte und dem
Verhältnis von Höhe zu Durchmesser ab.
Ob eine Schwimmlage stabil ist, kann die Funktion des
Drehmoments anzeigen, welches sich aus den Vektoren der
Gewichtskraft und der
Auftriebskraft für verschiedene Winkel ergibt.
Man kann an der Animation die Veränderungen der Drehmomente mit dem Winkel verfolgen.
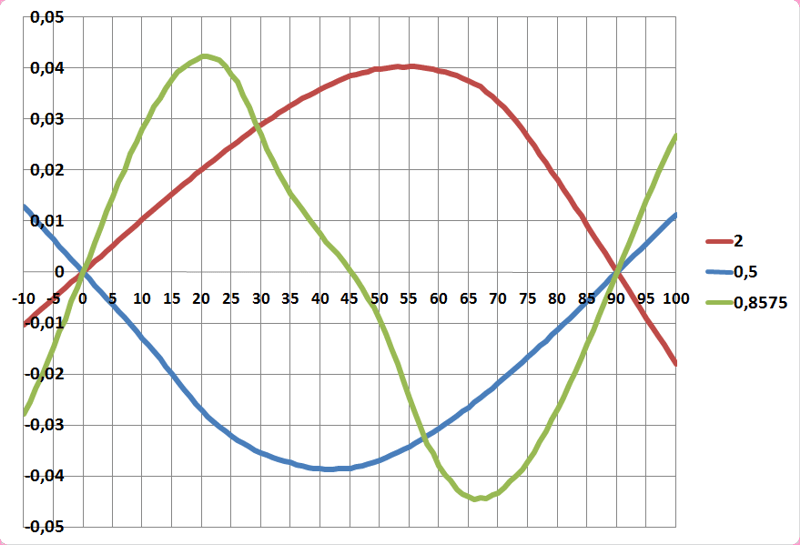
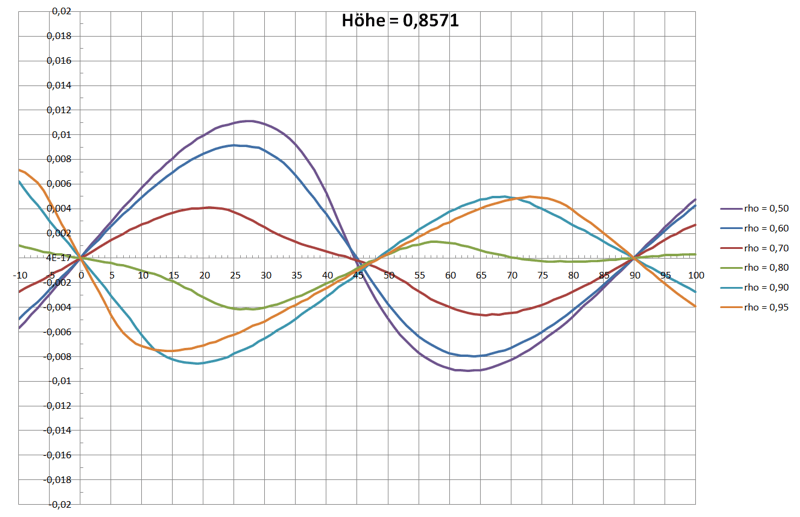
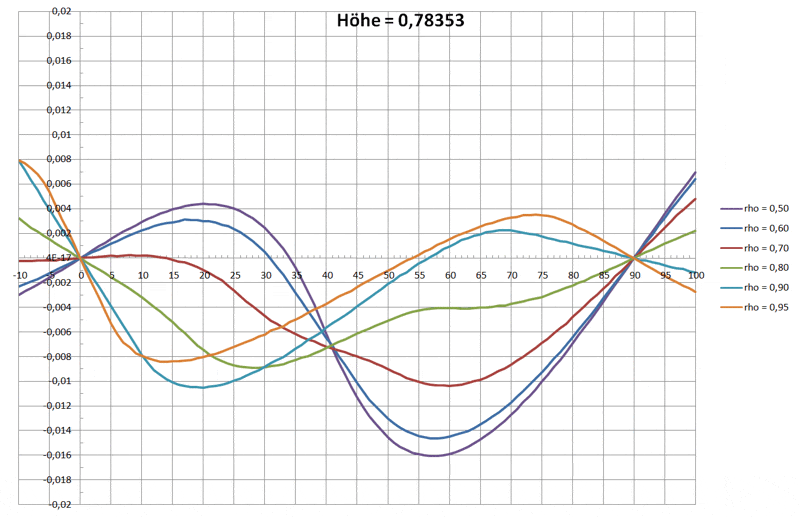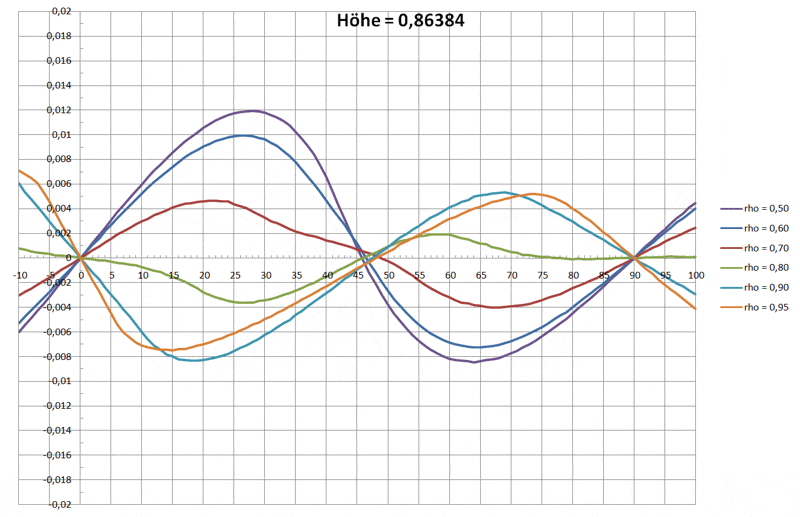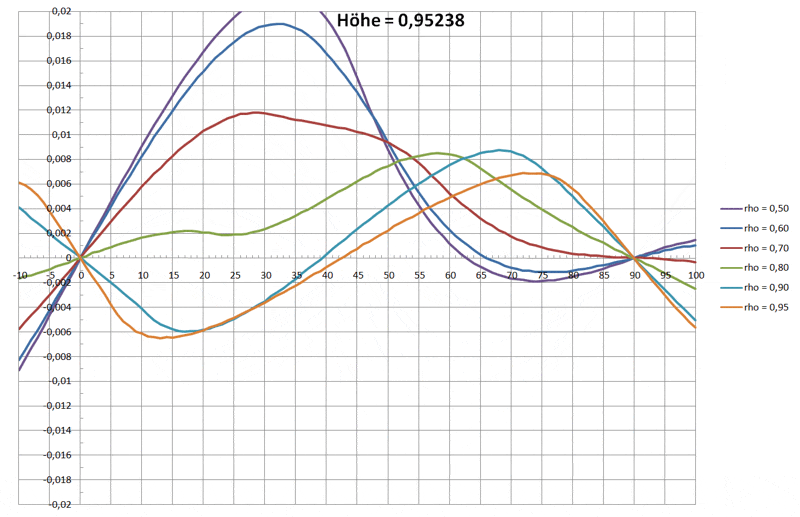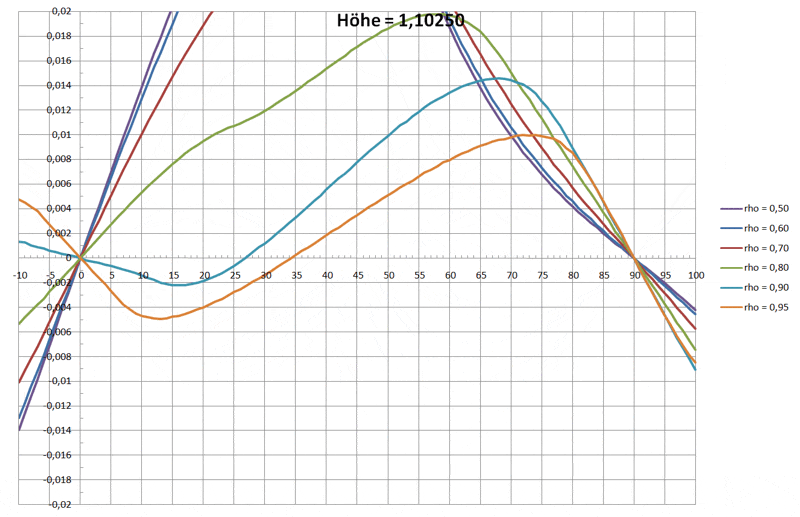
Den qualitativen Funktionsverlauf der drei Drehmomente über den Winkel sieht man in der folgenden Grafik:
Daraus wird auch klar, wie es zu stabilen Schwimmlagen kommt:
nur dort, wo der Funktionverlauf eine Nullstelle hat und gleichzeitig die erste Ableitung negativ ist, wird der Schwimmkörper zur Ruhe kommen.
Etwas anders formuliert:
1. Bedingung: das Drehmoment muss Null sein
2. Bedingung: es müssen rechts und links von diesem Punkt rücktreibende Drehmomente auftreten.
Aber wie kommt man an diese Drehmomentfunktionen?
Es gibt wie so oft mehrere Methoden.
Hier die erste.
3.) die praktische Findung
Man beschaffe sich ein Rundholz wie z.B. die abgebildete Teigrolle aus Buchenholz mit der Dichte 0,7 und schneide sie in verschieden dicke Scheiben.
Das Loch in der Mitte muss wasserdicht verschlossen werden.
Eine Füllung des Lochs mit Metallteilen erhöht die mittlere Dichte.
Dabei ist streng darauf zu achten dass der Schwerpunkt unverändert in der Mitte bleibt.
Die sehr dicken Scheiben schwimmen wie Baumstämme, die sehr dünnen Scheiben schwimmen wie Bierdeckel.
Dazwischen muss irgendwo der Übergang mit Schwimmlage bei 45° sein.
Also kürzt man die dicke Scheibe, bis man erfolgreich ist.
Hat man die richtige Abmessung gefunden beschwert man den Zylinder mit Eisenfeilspänen oder Bleikugeln (Gardinenband) bis sich die Schwimmlage bei 45° verflüchtigt.
Es bleiben zwei stabile Lagen bei 0° und bei 90°.
Man bestimmt nun noch die Dichte des Zylinders und ist fertig.
4.) rechnerische Näherungen
Man definiert ein festes dreidimensionales Koordinatensystem.
Darin wird der Schwerpunkt eines Zylinders in den Ursprung gelegt.
In der Ausgangslage liegt die Symmetrieachse des Zylinders auf der y-Achse (nach oben positiv).
Es erfolgen Drehungen um die z-Achse (das ist die Achse ins Papier hinein) in mathematisch positiver Richtung (entgegen dem Uhrzeigersinn).
Nach einer Drehung um 90° liegt die Symmetrieachse auf der x-Achse.
Der Vektor der Gewichtskraft bleibt vom Betrag konstant und liegt fest auf der y-Achse, weil auch der Schwerpunkt sich nicht verlagert.
Der Vektor der Auftriebskraft ist vom Betrag ebenfalls konstant, wandert aber dem Schwerpunkt des verdrängten Wassers folgend entlang der x-Achse in beiden Richtungen.
Die Ebene des Wasserspiegels variiert mit dem Drehwinkel und stellt sich immer so ein, das die verdrängte Wassermenge konstant bleibt.
Es läuft also bei der Berechnung nur darauf hinaus, die x-Position des Schwerpunkts der verdrängten Wassermenge zu berechnen.
Das ist auch gleichzeitig der Volumenanteil des Zylinders, der unter Wasser ist.
Absolute Werte sind nicht von Bedeutung, es kommt ja nur auf die Nullstellen und dem negativen Vorzeichen der Steigung für die stabile Lage an.
Auch die y-Position ändert nichts am Drehmoment und die z-Achse ist ganz aus der Betrachtung weil sich alles aus Symmetriegründen in der xy-Ebene abspielt.
Solange die vom Wasserspiegel erzeugte Schnittfläche durch den Zylinder eine Ellipse ist,
kann man noch mit relativ einfacher Mathematik die Berechnung der Höhe des Wasserspiegels berechnen.
Sind aber Schnitte durch Boden- und Deckelfläche dabei, ist das schon sehr schwierig.
Noch schwieriger ist die Bestimmung der Ortslage des Schwerpunkts, auch wenn nur der x-Wert von Interesse ist.
Wegen dieser und ähnlicher Probleme weiche ich oft auf numerische Verfahren aus.
Das bedeutet in diesem Fall, das nicht mit dem Volumen als Ganzes gerechnet wird, sondern mit sehr vielen zufällig ausgewählten Teilbereichen,
deren Eigenschaften dann am Ende zu einen Ergebnis wieder vereinigt werden.
Diese Methode wird auch als Monte-Carlo-Simulation bezeichnet.
Der Rechenaufwand steigt mit der Anzahl der Teilelemente und weil man eine hohe Genauigkeit anstrebt, muss die Teilezahl sehr hoch sein.
Daraus folgt, das man solche Rechnungen nicht mehr von Hand bewältigen kann,
obwohl die verwendete Mathematik sich im Wesentlichen auf addieren und multiplizieren beschränkt.
5.) Beschreibung der Methode
Man setzt einen Würfel mit der Kantenlänge 1 in das dreidimensionale Koordinatensystem, so dass der Mittelpunkt des Würfels im Ursprung liegt
und die Kanten parallel zu den Achsen des Koordinatensystem verlaufen.
Dann sind alle Punkte mit den Koordinaten (x,y,z) mit -0,5 < x|y|z < 0,5 im Innenraum des Würfels und alle anderen außerhalb.
Um daraus einen Zylinder zu definieren werden weitere Punkte ausgeschlossen, nämlich diejenigen, bei denen $x^2+y^2>0,25$ ist.
Unterschiedliche Höhen des Zylinders werden durch einen Faktor erreicht, mit dem die y-Koordinate zu multiplizieren ist.
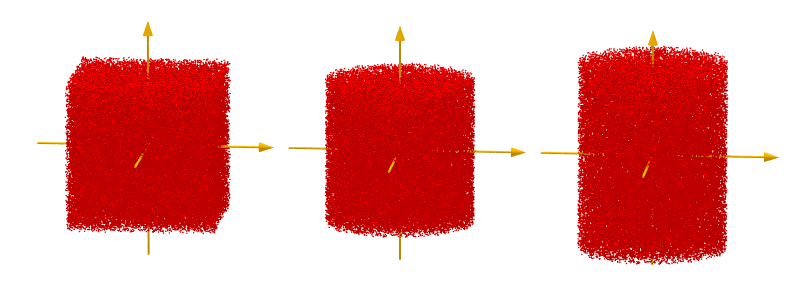
Nun erzeugt man sehr viele Punkte im inneren des Würfels, indem man jeweils drei Zufallszahlen im Bereich -0,5 bis 0,5 erzeugt (unten links),
Für den Zylinder (unten mitte) diejenigen mit $x^2+y^2>0,25$ nicht weiter beachtet,
und mit den anderen 78,54% weiter arbeitet, z.B. in y-Richtung um 30% streckt (unten rechts).
Die Anzahl der Punkte in den Bildern oben sind jeweils nur 100000.
Für ausreichende Genauigkeit sind mindestens die 10-fache Menge erforderlich.
Die Bearbeitung der Punkte beschränkt sich auf Strecken in y-Richtung und Drehen um die z-Achse.
Wenn man nun einen Zylinder mit der Höhe 0,8571 erzeugt und die einzelnen Punkte z.B. um den Winkel von 45° um die z-Achse dreht,
kann man den Wasserspiegel so einstellen, dass 70% der Punkte unter Wasser sind.
Diese Punkte werden in ihren x- und y-Koordinaten jeweils aufaddiert und die Summen am Ende durch die Anzahl dividiert.
So erhält man die Koordinaten des Schwerpunkts der verdrängten Wassermenge.
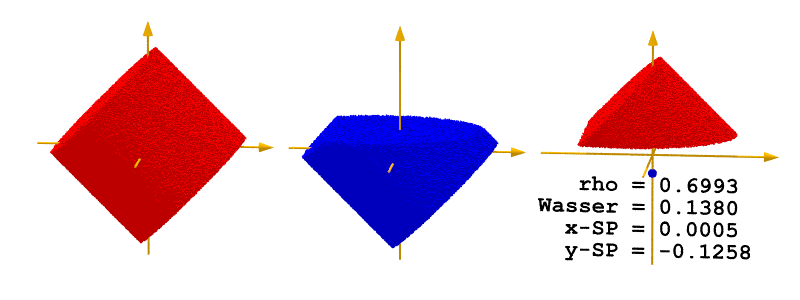
Die Bilder unten zeigen links den gedrehten Zylinder mit der Höhe 0,8571,
in der Mitte das verdrängte Wasservolumen und rechts den Teilkörper des Zylinders, der über der Wasseroberfläche bleibt.
Zudem ist der Schwerpunkt durch einem blauen Punkt markiert und die statistischen Daten von der Dichte,
der Höhe des Wasserspiegels und die Koordinaten des Schwerpunkts als Text ausgegeben.
Die Anzahl der verarbeiteten Punkte ist hier 1000000.
6.) Big Data
Da die Rechenmethode gute Ergebnisse liefert kann sie von der langsamen 3D-Grafik auf einen schnellen BASIC-Compiler übertragen werden.
Damit läuft die Berechnung um dem Faktor 1000 schneller.
So lassen sich für verschiedene Winkel, verschiedene Höhen und verschiedene Dichten in allen Kombinationen Drehmomente berechnen.
Damit bekommt man einen Überblick über das gesamte Problem.
Eine Darstellung der Datenflut in den 3 obigen Dimensionen ist kaum möglich, da für das jeweilige Ergebnis auch noch eine Dimension erforderlich sein muss.
Man kann dann nur noch auf die Zeit als Dimension ausweichen und somit einen Film erstellen, der in den einzelnen Bilder eines Datengebirges die Dichte variiert.
Für diesen Film waren 7*71*101=50197 Berechnungen erforderlich mit jeweils 500*500*500=125000000 Punkten.
Das hat der Rechner auf 4 Kerne verteilt in 38,8 Stunden erledigt.
Was kann man nun mit diesem Datenberg machen?
7.) die Rätsellösungen
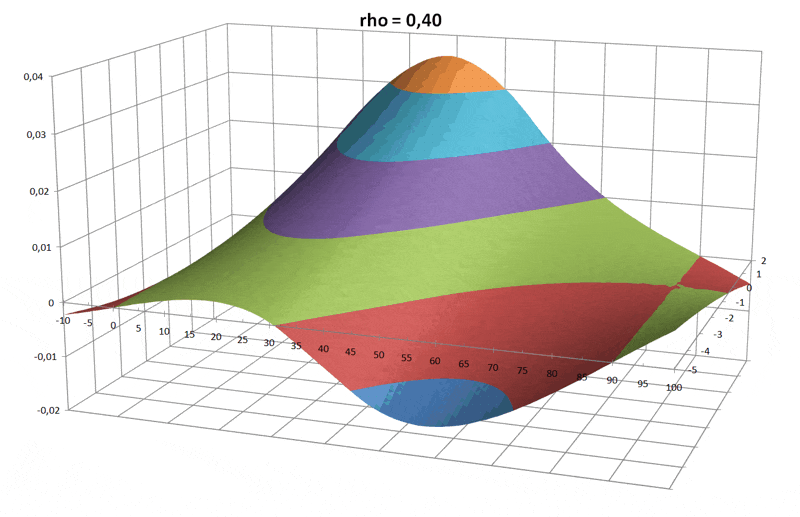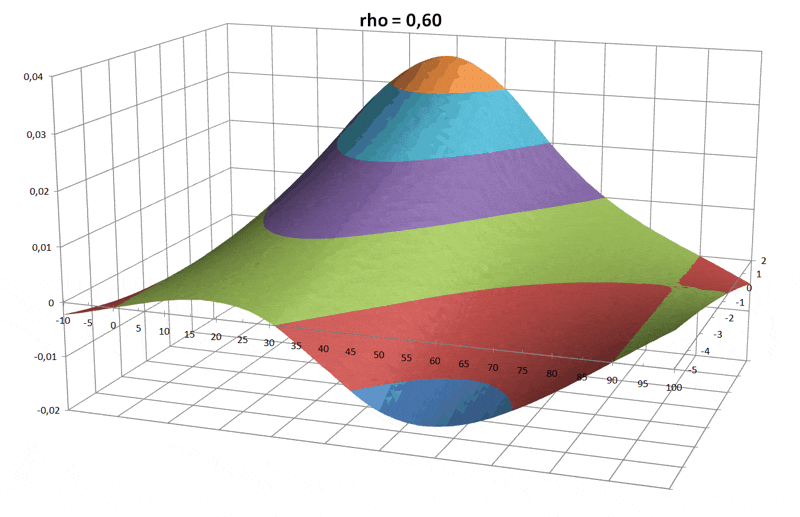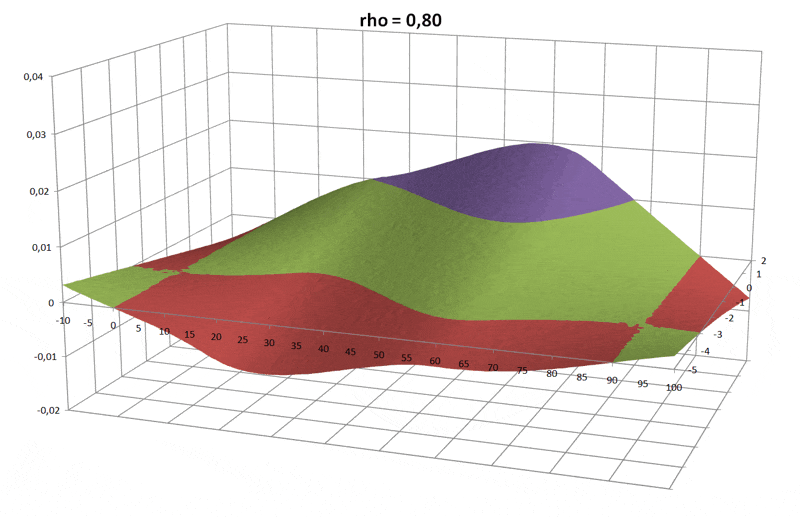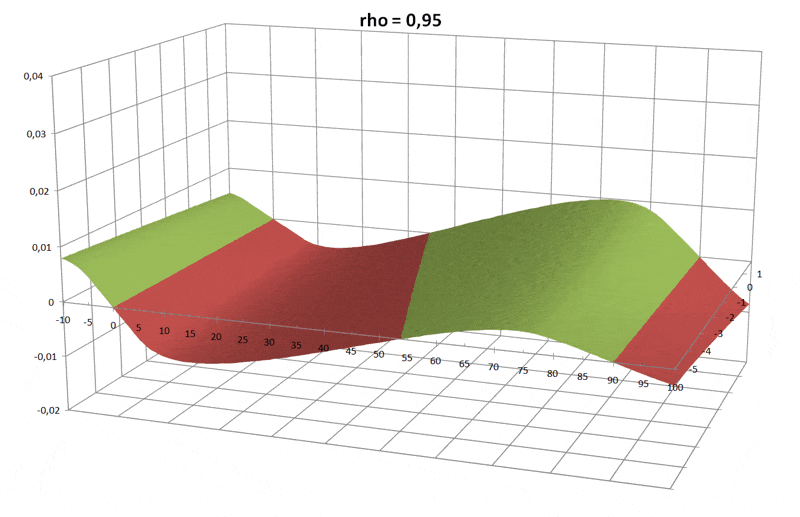
Wenn man Schnitte durch den Datenwürfel macht, findet man schnell die gefragten Lösungen.
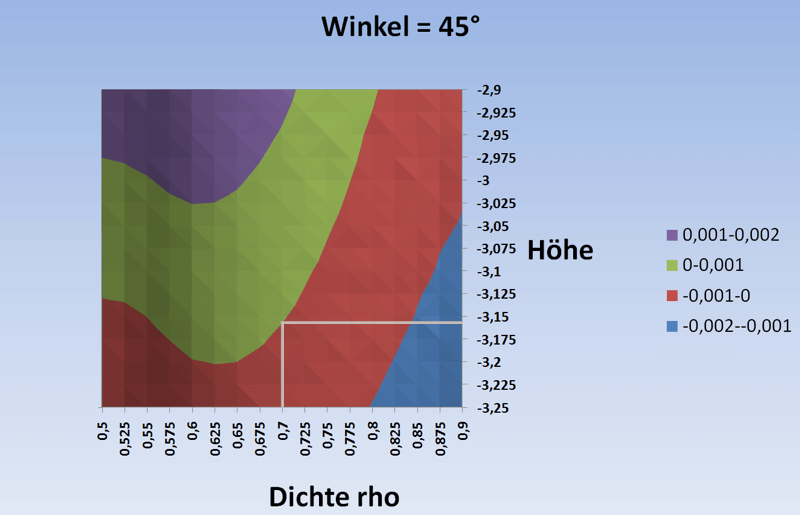
ein Schnitt bei einem Winkel von 45° zeigt die Höhe-Dichte-Ebene:
Man findet die Grenzlinie zwischen grün = positiv und rot = negativ.
Wenn man ausgehend von der vorgegebenen Dichte $\rho=0,7$ senkrecht zur Grenzlinie geht und von dort waagerecht bis zur Höhenskala,
die hier wie auch in obigem Film als Logarithmus zur Basis 1,05 beschriftet ist,
liest man den Wert -3,16 ab und rechnet das in das Verhältnis Höhe zu Durchmesser um:
$$\rand{
\frac{Höhe}{Durchmesser}=1,05^{-3,16}=0,8571 }$$
Ein zweiter Schnitt an der Stelle -3,16 zeigt die Winkel-Dichte-Ebene.
Es sind nur die Grenzlinien gezeigt.
Die gefüllten Flächen würden sich überschneiden.
$$\rand{
zwei\;stabile\;Lagen\;bei\quad \rho>0,8 \quad und \quad \rho<0,2
}$$
Zum Schluss noch eine Übersicht über die Schwimmlagen mit verschiedenen Höhen.
Der Film zeigt die Entwicklung der Schwimmlagen im Übergang zwischen Bierdeckel und Baumstämmen.