1.) Vereinigung von Flächen mit resultierendem Schwerpunkt
Bei der Vereinigung von zwei Flächen mit bekanntem Schwerpunkt hilft das Prinzip einer Balkenwaage weiter. Der Balken ist dabei die Strecke von einem Schwerpunkt zum anderen. Die Aufhängung muss dann so gewählt werden, dass die Drehmomente auf beiden Seiten gleich groß sind, also $m_1\cdot l_1=m_2\cdot l_2$.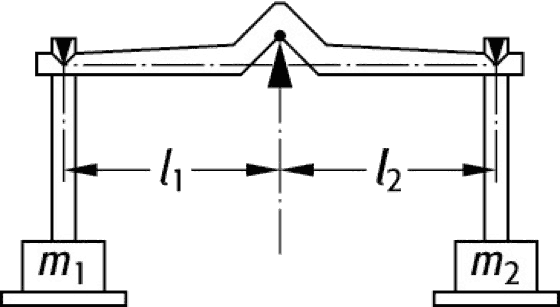
Hier muss nur die Masse durch den Flächeninhalt ersetzt werden. Der Aufhängepunkt ist dann der resultierende Schwerpunkt.
2.) die Flächen des Rätsels und ihre Schwerpunkte
Wenn man sich die Symmetrie der obigen animierten Grafik ansieht findet man, dass alle Schwerpunkte auf der y-Achse liegen und also auch der Waagbalken. An die linke Seite der Waage soll der Halbkreis hängen und an der rechten Seite die hellblau Rätselfläche. Diese beiden vereint ergeben das Rechteck. $$\sand{\begin{align} F_{Halbkreis}\cdot l_1&=F_{Rätselfläche}\cdot l_2 \\ l_1&=y_{Rechteck}-y_{Halbkreis} \\ l_2&=y_{Rätselfläche}-y_{Rechteck} \\ F_{Halbkreis}&=\frac12\pi r^2 \\ F_{Rätselfläche}&=2-\frac12\pi r^2 \\ y_{Rechteck}&=\frac12 \\ y_{Halbkreis}&=\frac{4r}{3\pi}\quad\text{(aus Formelsammlung)} \\ y_{Rätselfläche}&=r\quad\text{(Forderung des Rätsels)} \end{align}}$$ Wenn man alles in die erste "Balken"-Gleichung einsetzt ergibt sich eine Bestimmungsgleichung für $r$: $$\rand{ (3\pi-4)r^3-12r+6=0 }$$3.) die Berechnung
Das obige Ergebnis kann man als Funktion $f(r)$ in einem Diagramm darstellen: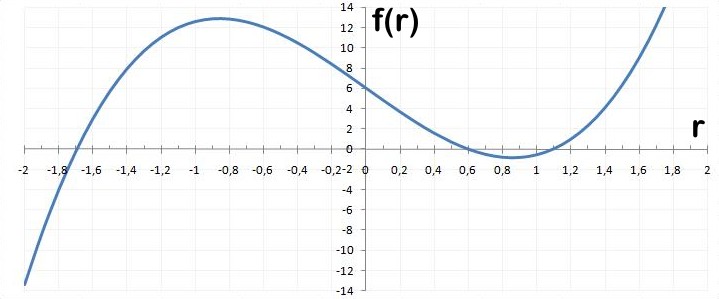
So sieht man, dass es drei reelle Nullstellen gibt, etwa bei $r=-1,7\quad r=0,6\quad r=1,1$. Zur genaueren Bestimmung kann man sich mit dem Newton-Verfahren schrittweise nähern: $$\sand{ r_{n+1} = r_n - \frac{f(r_n)}{f'(r_n)} = r_n - \frac{(3\pi-4){r_n}^3-12r_n+6}{3(3\pi-4){r_n}^2-12} }$$
Dazu sind als Startwerte die obigen ungefähren Nullstellen zu nehmen. Umso genauer die Anfangswerte bekannt sind umso schneller konvergiert das Ergebnis. Jeder Näherungsschritt verdoppelt die Genauigkeit.
Die folgenden 3 Tabellen zeigen den Ablauf der Näherung.
| $n$ | $r_n$ |
|---|---|
| 0 | -1,7000000000000000000000000000000000000000 |
| 1 | -1,6928086267140545037902417428692267808188 |
| 2 | -1,6927673753403919553762594653805110560346 |
| 3 | -1,6927673739867982875224838914655889125510 |
| 4 | -1,6927673739867982860650761994187465313627 |
| 5 | -1,6927673739867982860650761994187465296732 |
| $f'(r)$ | 34,6334752645937870601806951804544837120586 |
| $n$ | $r_n$ |
|---|---|
| 0 | 0,6000000000000000000000000000000000000000 |
| 1 | 0,5954002837565605348709257518771503519048 |
| 2 | 0,5954333562398792019177573384697966964291 |
| 3 | 0,5954333579410975484834038957724753031334 |
| 4 | 0,5954333579410975529849597728672635177991 |
| 5 | 0,5954333579410975529849597728672635493178 |
| $f'(r)$ | -6,2300832829399959127476805426944077967670 |
| $n$ | $r_n$ |
|---|---|
| 0 | 1,1000000000000000000000000000000000000000 |
| 1 | 1,0973505441809740108504377410395533981306 |
| 2 | 1,0973340166878569277320228818918832340707 |
| 3 | 1,0973340160457007340495179497276833174765 |
| 4 | 1,0973340160457007330801164265514829825646 |
| 5 | 1,0973340160457007330801164265514829803554 |
| $f'(r)$ | 7,5966080183462088525669853622399240847083 |
Da $r$ nur in den Grenzen von 0 bis 1 definiert ist, kommt nur die zweite Lösung als Ergebnis dieses Rätsels infrage. Die dazugehörige grafische Darstellung sieht dann so aus: $$\begin{align} \text{grün:}&\quad & y_{Rätselfläche}&=0,595433 \\ \text{gelb:}&\quad & y_{Rechteck}&=0,500000 \\ \text{rot:}&\quad & y_{Halbkreis}&=0,252710 \end{align}$$