Zur Bearbeitung dieses Rätsels ist ein Astronomieprogramm mit hoher Genauigkeit erforderlich.
Davon findet man viele im Internet, allerdings mit recht unterschiedlicher Qualität.
Sofern nicht schon etwas passendes vorhanden ist, ist der einfachste Weg zur Lösung dieses Rätsels
die Benutzung des auf dieser Seite zum Download bereitgestellten Programms Astrozeit.
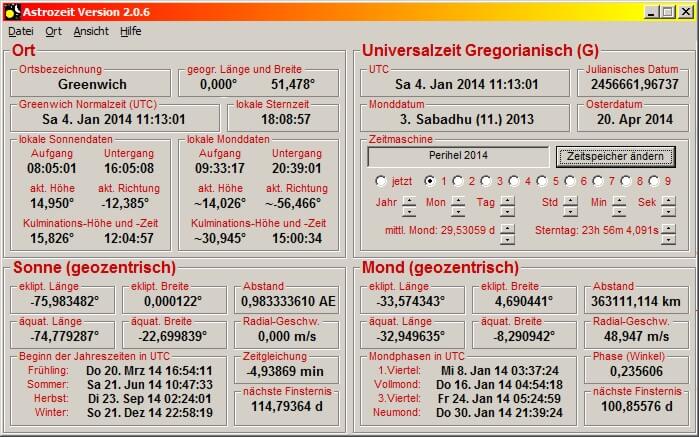Abbildung 1
Die Lösung des Problems lässt sich in Teilaufgaben zerlegen:
- 1) die Sonne muss in kürzester Zeit die Strecke von zwei mal 18° auf der Ekliptik zurücklegen.
Die Aufgabe: wo liegt die Strecke und welche Zeitpunkte liegen am Ende der Strecke.
- 2) zu den unter 1) gefundenen Zeitpunkten müssen die Orte gefunden werden, bei denen die zwei folgenden Bedingungen erfüllt sein müssen:
- die Ekliptik muss für beide Orte zur jeweiligen Zeit am Horizont senkrecht stehen
- die Sonne muss exakt 18 Grad unter dem Horizont stehen, beim ersten Zeitpunkt am Westhorizont, beim zweiten am Osthorizont
Punkt 1)
Über das Jahr gemittelt ist die Zeit, die die Sonne auf der Ekliptik für 36° braucht:
tmittel = Jahreslänge * 36° / 360° = 36,52425 Tage
Das ist leicht zu unterbieten.
Für eine vorgegebene Strecke auf der Ekliptik ist die Zeit dann minimal,
wenn die Sonne sich mit maximaler Geschwindigkeit relativ zur Fixsternsphäre bewegt.
Das ist in der Nähe des Perihels der Fall.
Also stellt man den Zeitpunkt des Perihels in die Mitte der Strecke (mit der Radialgeschwindigkeit der Sonne = 0, siehe die Einstellung der Zeitmaschine in Abbildung 1),
liest die ekliptikale Länge der Sonne ab und sucht nach den beiden Zeitpunkten,
die jeweils 18° ekliptikaler Länge davon entfernt sind.
Da der frühere Zeitpunkt im Dezember ist, der ja schon für dieses Rätsel nicht mehr in der Zukunft liegt,
muss das Perihel von 2014 gewählt werden.
Zeitpunkt des Perihels 2014 = 4.1.2014 11:13:01
ekliptikale Länge des Perihels 2014 = -75,983482°
ekliptikale Länge des 1. Zeitpunktes = -93,983482°
Zeitpunkt des 1. Zeitpunktes = 17.12.2013 19:12:39
ekliptikale Länge des 2. Zeitpunktes = -57,983482°
Zeitpunkt des 2. Zeitpunktes = 22.1.2014 03:22:55
Nun lässt sich auch die minimale Zeit für den Sonnenlauf über 36° angeben:
tminimal = 35,34046 Tage
und das ist deutlich kürzer als der oben errechnete mittlere Wert.
Damit wäre der Punkt 1) erledigt, wenn man es nicht auf die Spitze treiben will. Hier also nur ein Hinweis für Spezialisten.
Da unser Mond die Erde ein wenig herumschleudert, bewegt sie sich im Monatsrhythmus etwas schneller und dann wieder etwas langsamer.
Das führt aus geozentrischer Sicht zu einer etwas ungleichmäßigen Geschwindigkeit der Sonne.
Es ist auch schon an den beiden Zeiten für das Durchlaufen der 18° eine Unsymmetrie zu erkennen.
der Zeitraum t1 = 17,66693 Tage ist erkennbar kürzer als t2 = 17,67354 Tage.
Wenn man sich die Funktion des Sonnenabstands über die Zeit aufträgt fällt noch keine Unsymmetrie auf,
aber nimmt man noch die erste Ableitung nach der Zeit, also die Radialgeschwindigkeit, hinzu,
dann erkennt man eine kleine Sinuskurve über der ansonsten fast geraden Geschwindigkeitsfunktion (siehe Abbildung 2).
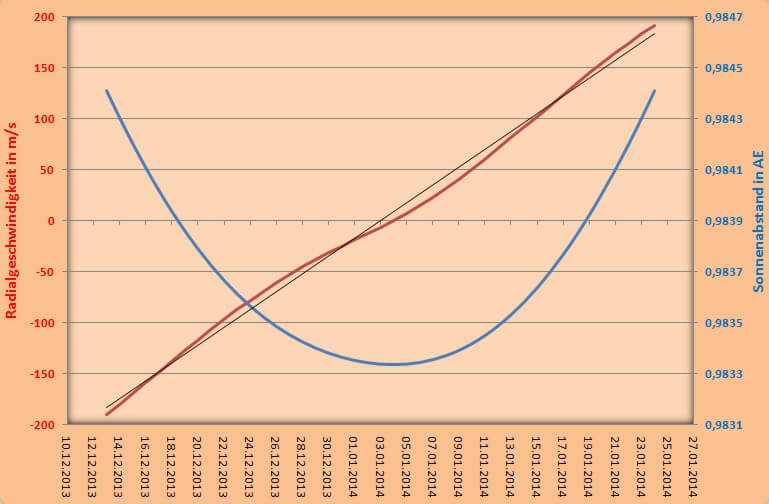Abbildung 2
Das führt dazu, dass es einen wirklichen zeitlichen Minimalwert für den 36°-Weg der Sonne gibt,
der überraschenderweise einige Stunden gegen den obigen verschoben ist.
Da es sich um ein sehr flaches Minimum handelt,
spart man nur eine viertel Sekunde mit dem Ersatzzeitpunkt = 04.01.2014 07:50:00 anstelle des echten Perihels.
Punkt 2)
Die beiden Zeitpunkte der Himmelsaufnahmen (ich nehme die des echten Perihels) liegen nun vor.
Die zugehörige Himmelskonstellation ist nun die folgende:
die erste Aufnahme hat als Rand den Horizont, auf dem der Perihelpunkt im Westen liegt.
Die Ekliptik muss durch den Zenit gehen, wenn sie am Horizont senkrecht stehen soll.
Der Mittelpunkt der Aufnahme ist der Zenit und man kann dafür leicht die ekliptikalen Koordinaten angeben:
die ekliptikale Länge ist um 90° größer als der entsprechende Wert des Perihels.
Für die zweite Aufnahme gilt ähnliches: "Westen" wird durch "Osten" ersetzt und "90° größer" durch "90° kleiner".
ekliptikale Länge des Perihels 2014 = -75,983482°
ekliptikale Länge des Zenits des 1. Zeitpunktes = 14,016518°
ekliptikale Länge des Zenits des 2. Zeitpunktes = -165,983482°
Die zugehörige ekliptikale Breite ist für alle Punkte Null, weil die Punkte alle auf der Ekliptik liegen.
Nun müssen die ekliptikalen Koordinaten in äquatoriale Koordinaten umgewandelt werden.
Mit Hilfe des Programms Astrozeit stellt man die Sonne mit der Zeitmaschine so ein, dass sie nacheinander auf den beiden Zenitpunkten steht.
Das findet zwar in jedem Jahr statt, aber man sollte zum Perihel zeitnahe Einstellungen benutzen,
weil über viele Jahre hinweg die Schiefe der Ekliptik und der Frühlingspunkt sich leicht verändern.
Die Ablesung der neuen Koordinaten ergibt:
äquatoriale Länge (Rektaszension) des Zenits des 1. Zeitpunktes = 12,900409°
äquatoriale Breite (Deklination) des Zenits des 1. Zeitpunktes = 5,528174°
äquatoriale Länge (Rektaszension) des Zenits des 2. Zeitpunktes = -167,099591°
äquatoriale Breite (Deklination) des Zenits des 2. Zeitpunktes = -5,528174°
Das sind zunächst natürlich noch Himmelskoordinaten,
aber die gesuchten geografischen Koordinaten sind auf Grund der Erdrotation nur gegen die Himmelskoordinaten verdreht.
Es gibt täglich eine exakte Übereinstimmung der beiden Nullmeridiane nämlich dann, wenn in Greenwich auf dem Nullmeridian die lokale Sternzeit 00:00:00 ist.
Dabei muss zusätzlich berücksichtigt werden, dass die Zählrichtung umgekehrt ist, also die Werte der Längen bei der Umwandlung mit -1 multipliziert werden müssen.
Stellt man nun für beide Aufnahmezeitpunkte einen Ort mit der geografischen Länge Null (z.B. Greenwich) ein, kann man die lokale Sternzeit ablesen.
lokale Sternzeit für Greenwich des 1. Zeitpunktes = 00:58:56 = 14,733112°
lokale Sternzeit für Greenwich des 2. Zeitpunktes = 11:28:32 = 172,133441°
Der jeweils erhaltene Winkel wird zur negativen äquatorialen Länge hinzugefügt und man erhält die geografische Länge der Aufnahmeorte.
An der Breite ändert sich nichts. Die irdischen Aufnahmekoordinaten sind also:
geografische Länge des 1. Aufnahmeorts = 1,832703°
geografische Breite des 1. Aufnahmeorts = 5,528174°
geografische Länge des 2. Aufnahmeorts = -20,766968°
geografische Breite des 2. Aufnahmeorts = -5,528174°
Damit sind alle Fragen des Rätsels beantwortet.
Es ist vielleicht noch von Interesse, ob die ermittelte minimale Zeitspanne zwischen den Aufnahmezeitpunkten in jedem Jahr gleich ist.
Darauf gibt die nachfolgende Tabelle Auskunft:
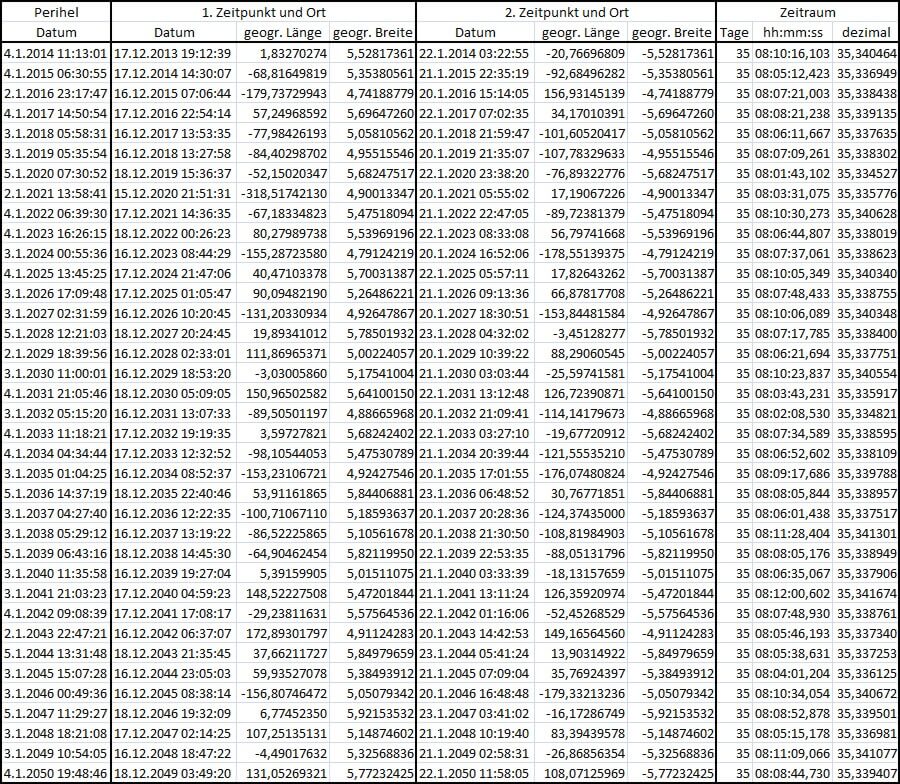Abbildung 3
Der Schwankungsbereich liegt bei etwa 10 Minuten.
Auch die geografische Breite ist sehr stabil bei 5°.
Die geografische Länge ist über den gesamten Umfang der Erde verteilt,
aber der räumliche Abstand der beiden Orte,
der direkt von der Länge des Zeitraums abhängt ist natürlich wieder recht stabil bei etwa 22,5°
Diese Informationen wurden zusammengestellt von