Lösungsbeschreibung des Preisrätsels vom Mai 2014

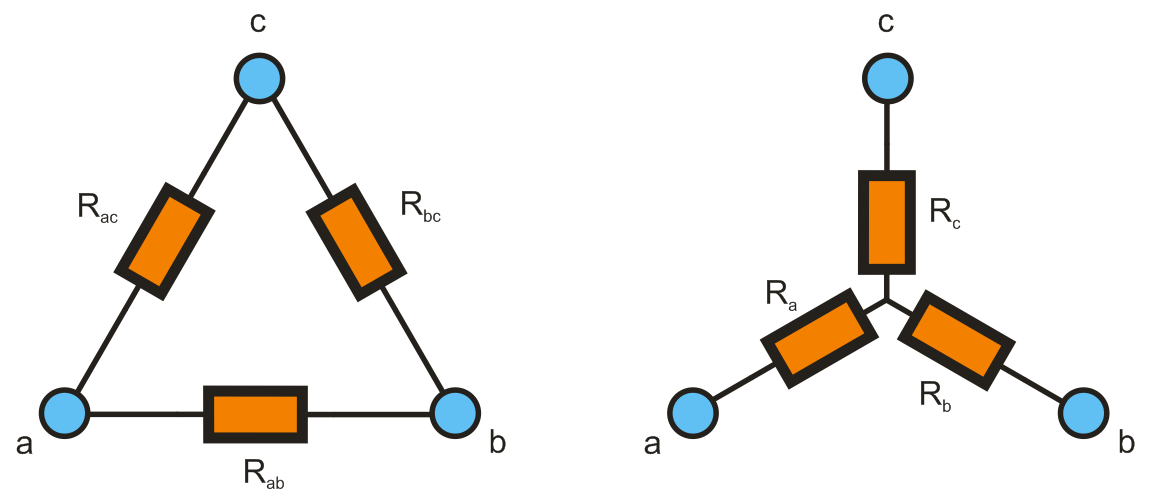
Widerstandsnetzwerk

Der klassische Weg, ein Widerstandsnetzwerk zu berechnen, ist die Zusammenfassung verschiedener Widerstände in Reihen- und Parallelschaltung zu einem resultierenden Widerstand.

1.) die Parallelschaltung

$$\sand{R_{ges}=\frac {R_1R_2}{R_1+R_2}}$$

2.) die Reihenschaltung

$$\sand{R_{ges}=R_1+R_2}$$ Bei vielen Netzwerken ist aber noch weiteres zu tun, weil sich nicht alles durch Reihen- und Parallelschaltung auf einen resultierenden Widerstand reduzieren lässt.

3.) die Stern-Dreieck-Umwandlung

Dreieck zu Stern:	$R_{a}={\frac {R_{{ac}}R_{{ab}}}{R_{{ac}}+R_{{ab}}+R_{{bc}}}}$
	$R_{b}={\frac {R_{{ab}}R_{{bc}}}{R_{{ac}}+R_{{ab}}+R_{{bc}}}}$
	$R_{c}={\frac {R_{{ac}}R_{{bc}}}{R_{{ac}}+R_{{ab}}+R_{{bc}}}}$

Stern zu Dreieck:	$R_{{ac}}={\frac {R_{a}R_{b}+R_{b}R_{c}+R_{c}R_{a}}{R_{b}}}$
	$R_{{ab}}={\frac {R_{a}R_{b}+R_{b}R_{c}+R_{c}R_{a}}{R_{c}}}$
	$R_{{bc}}={\frac {R_{a}R_{b}+R_{b}R_{c}+R_{c}R_{a}}{R_{a}}}$

An einem einfachen Beispiel soll der klassische Vorgang erläutert werden. Im folgenden Bild A ist ein Widerstandsnetzwerk aus 7 gleichen Widerständen dargestellt, alle mit dem Widerstandswert 1. Eine Vereinfachung durch Zusammenfassung von parallelen oder in Reihe geschalteten Widerständen ist zunächst nicht möglich. Deshalb ist der erste Schritt eine Umwandlung der blauen in Sternschaltung vorliegenden Widerstände in die Dreiecksform. Das Bild B zeigt das Ergebnis in Form der gelben Widerstände. Diese erhalten gemäß der obigen Transformationsgleichung nun alle den Widerstandswert 3. Nun können zweimal jeweils zwei Widerstände in Parallelschaltung zusammengefasst werden und ergeben die in Bild C grünen Widerstände mit dem Wert 3/4. Eine weitere Umwandlung überführt die beiden grünen und den gelben Widerstand in Dreieckschaltung zu einem Stern. Das Bild D zeigt das Resultat, wobei sich für die grünen Widerstände den Wert 1/2 und für den gelben den Wert 1/8 berechnen lässt. Nun ist alles Übrige mit Reihen- und Parallelschaltung zu berechnen. Die in Reihe befindlichen linken Widerstände haben zusammen den Wert 9/8 und werden parallel zu der rechten Reihenschaltung mit dem Wert 3/2 zum Gesamtwert von 9/14 zusammengefasst. Mit dem in Reihe liegenden Widerstand 1/2 ist dann das Endergebnis 8/7. Insgesamt sind zwei Stern-Dreieck-Umwandlungen, 3 Parallelschaltungen und 3 Reihenschaltungen auszurechnen.

Man kann das Berechnen besonders von Netzwerken mit gleichen Widerständen aber auch auf eine völlig andere Art vornehmen. Dazu betrachte man das folgende Bild unten. Man stelle sich vor, die Flächen seien aus Widerstandsfolie gefertigt. Alle Quadrate haben den gleichen Widerstand, gemessen von der oberen Kante zur unteren. Das mag auf den ersten Blick verwirren, aber ein größeres Quadrat hat eine größere Höhe, was einen größeren Widerstand erzeugt (entspricht der Reihenschaltung) als auch eine größere Breite, was einen geringeren Widerstand erzeugt (entspricht der Parallelschaltung). Beides kompensiert sich also. Deshalb haben alle Folienelemente mit gleichem Seitenverhältnis auch einen gleichen Widerstand. Wer genau hinschaut, erkennt in der Anordnung der quadratischen Folienwiderständen das Widerstandsnetzwerk aus dem obigen Bild A wieder. Wenn nun die Fläche vollständig durch Quadrate zu einem Rechteck ausgefüllt ist, kann man den Gesamtwiderstand aus dem Seitenverhältnis des Rechtecks sofort ablesen: 8 zu 7, und damit hat man das gleiche Ergebnis wie oben mit erheblich größerem Aufwand berechnet wurde, auf elegante geometrische Weise sehr einfach gelöst.

Die einzige Aufgabe besteht darin, eine Umsetzung des Widerstandsnetzwerks in die Folienform mit quadratischen Widerstandselementen vorzunehmen. Das fällt uns Menschen mit einem Blick für Zusammenhänge aber nicht sehr schwer. Zudem kann man mit zunächst unbekannten Abmessungen einfache lineare Gleichungen aufstellen und so die Größe der Quadrate berechnen.

Hier nun das in diesem Monatsrätsel vorgegebene Widerstandsnetzwerk und das Äquivalent in Folie. Dabei waren die Nummern an den Widerständen eine zusätzliche Hilfe für diejenigen, die auf dem Weg zu dieser Art von Lösung waren.

Aus dieser graphischen Umsetzung des Widerstandsnetzwerks lassen sich alle Antworten auf die Rätselfragen sofort ablesen:

da die gesamte Fläche auch ein Quadrat (112x112) ist, ist der resultierende Widerstand gleich dem Wert eines der 21 gleichen Einzelwiderstände des Widerstandsnetzwerks.
da der Punkt B auf der Linie unterhalb des Quadrats mit der Kantenlänge 50 liegt, die Gesamthöhe des Quadrats aber 33+29+50=112 ist, ist Spannung am Punkt B =(112-50)/112=31/56 der Spannung von A nach Null.
Die gleiche Überlegung gilt für den Punkt C: 53/112 der Spannung von A nach Null.

Diese Informationen wurden zusammengestellt von

Kurzbewertung dieser Information:
sehr gut	gut	befriedigend
ausreichend	mangelhaft	ungenügend