1.) der strenge Weg zum Ziel
Die Mantelfläche eines Rotationskörpers die durch Rotation einer Funktion $y=f(x)$ im Bereich $x_{min}$ bis $x_{max}$ um die x-Achse erzeugt wird, lässt sich berechnen mit $$\sand{M=2\pi\cdot\intop_{x_{min}}^{x_{max}} y\cdot\sqrt{1+(y')^2}\;dx}$$ Die Funktion ist eine Hyperbel mit der impliziten Form $$\sand{\left(\frac ya\right)^2=\left(\frac xb\right)^2+1}$$ $$\text{daraus folgt}\quad\sand{y=f(x)=a\cdot\sqrt{1+x^2/b^2}}$$ $$\text{und die Ableitung}\quad\sand{y'=\frac a{b^2}\cdot\frac x{\sqrt{1+x^2/b^2}}}$$ Man bildet nun durch Einsetzen das Integral in den Grenzen von $0$ bis $h$, was der Hälfte des gesuchten Mantels entspricht. $$\sand{\frac{M(x)}2=2\pi\intop_0^h a\cdot\sqrt{1+x^2/b^2}\cdot\sqrt{1+\frac {a^2} {b^4}\cdot\frac {x^2}{1+x^2/b^2}}\;dx}$$ $$\text{und vereinfacht}\quad\sand{\frac{M(x)}2=2\pi a\intop_0^h\sqrt{1+x^2\cdot\left(\frac{b^2+a^2}{b^4}\right)}\;dx}$$ $$\text{mit der Ersetzung}\quad\sand{k^2=\frac{a^2+b^2}{b^4}}\quad\text{wird das Integral übersichtlicher und leichter lösbar:}$$ $$\sand{\frac{M(x)}2=2\pi a\intop_0^h\sqrt{1+x^2k^2}\;dx =\pi a\cdot\left(h\sqrt{k^2h^2+1}+\frac1{k}\arsinh\left(hk\right)\right)=\frac{M(a,h,k)}2}$$ Für das Lösen solcher Integrale kann man auf Formelsammlungen zurückgreifen aber einfacher ist, den Computer, der mit dem Internet verbunden ist, selbst zum Berechnen heranzuziehen. Es bieten sich einige Internetseiten zur kostenlosen Nutzung dafür an:matheguru.com oder integralrechner oder Online Integralrechner WolframAlpha
Auch für die Berechnung von Ableitungen gibt es entsprechende Seiten:matheguru.com/rechner/ableiten oder ableitungsrechner
Die Rechenzeit ist teilweise begrenzt. Deshalb ist es sinnvoll, die einzugebende Funktion soweit wie möglich zu vereinfachen.Nun ist es an der Zeit die Werte für $a$, $h$ und $k$ in Abhängigkeit vom Winkel $\alpha$ zu bestimmen und in die vorangegangene Gleichung zu setzen. Dabei ist die weitere Voraussetzung das Verhältnis Abstand $d$ zu Streckenlänge $s$ von 1 : 4. Da für die Lösung des Rätsels die absolute Größe ohne Bedeutung ist kann man mit beliebigen Einheiten rechnen. Deshalb wird hier $d=1$ und $s=4$ im weiteren Verlauf angenommen und die Mantelfläche auf diese Festlegung bezogen in Quadrateinheiten angegeben. $$\sand{a=d=1}$$ $$\sand{h=s/2\cdot \cos \alpha=2\cdot \cos \alpha}$$ und aus der Hyperbelgleichung nach $b$ aufgelöst und für $x=h$ und $y=r$ (dem maximalen Radius) eingesetzt $$\sand{b=\frac h{\sqrt{\left({\displaystyle\frac ra}\right)^2-1}} =\frac{s/2\cdot\cos\alpha}{{\sqrt{\left({\frac{\sqrt{a^2+\left(s/2\cdot\sin\alpha\right)^2}}{\displaystyle a}}\right)^2-1}}}=\cot\alpha}$$ $$\sand{k=\frac{\sqrt{a^2+b^2}}{b^2}=\tan\alpha\cdot\frac{\sqrt{1+\cot^2\alpha}}{\cot\alpha}=\frac{\tan\alpha}{\cos\alpha}}$$ Durch Einsetzen ergibt sich dann $$\sand{\frac{M(\alpha)}2=2\pi\cdot{\textstyle\sqrt{3\cdot\sin^2\alpha+1}}+\pi\cdot\cot\alpha\cdot\cos\alpha\cdot \arsinh\left({\textstyle2\cdot \tan\alpha}\right)}$$ oder mit $\ln(x+\sqrt{x^2+1})=\arsinh(x)$ $$\sand{\frac{M(\alpha)}2=2\pi\cdot{\textstyle\sqrt{3\cdot\sin^2\alpha+1}}+\pi\cdot \cot\alpha\cdot\cos\alpha\cdot\ln\left(\frac{\sqrt{3\cdot\sin^2\alpha+1}+2\cdot\sin\alpha}{\cos\alpha}\right)}$$ und die Ableitung $$\sand{\begin{eqnarray}\frac d{d\alpha}\frac{M(\alpha)}2=0={\textstyle-}{\textstyle\pi}{\textstyle\cdot}\frac{cos^3\alpha}{\sin^2\alpha}\cdot{\textstyle\ln}\frac{\sqrt{3\cdot\sin^2\alpha+1}+2\cdot\sin\alpha}{\cos\alpha} \\ -2\pi\cdot\cos\alpha\cdot{\textstyle\ln}\frac{\sqrt{3\cdot\sin^2\alpha+1}+2\cdot\sin\alpha}{\cos\alpha} \\ +{\textstyle\pi}{\textstyle\cdot}\frac{cos^2\alpha}{\sin\;\alpha}{\textstyle\cdot}{\textstyle\left(\frac{\frac{3\cdot\cos\alpha\cdot\sin\alpha}{\sqrt{3\cdot\sin^2\alpha+1}} +2\cdot\cos\alpha}{\sqrt{3\cdot\sin^2\alpha+1}+2\cdot\sin\alpha}+\frac{\sin\alpha}{\cos\alpha}\right)} +\frac{6\pi\cdot\cos\alpha\cdot\sin\alpha}{\sqrt{3\cdot\sin^2\alpha+1}}\end{eqnarray}}$$ Spätestens hier ist ein Ende der klassischen Mathematik erreicht denn diese letzte Gleichung ist nicht nach $\alpha$ aufzulösen. Um aber doch noch zu einem Ergebnis zu kommen lässt sich diese Gleichung auf ein EXCEL Tabellenblatt übertragen und mit dem Solver lösen. Das Ergebnis ist: $$\rand{\text{maximale Mantelfläche = 26,3113090834369 bei einem Winkel von 50,0929415436324 Grad}}$$
2.) der andere Weg zum Ziel
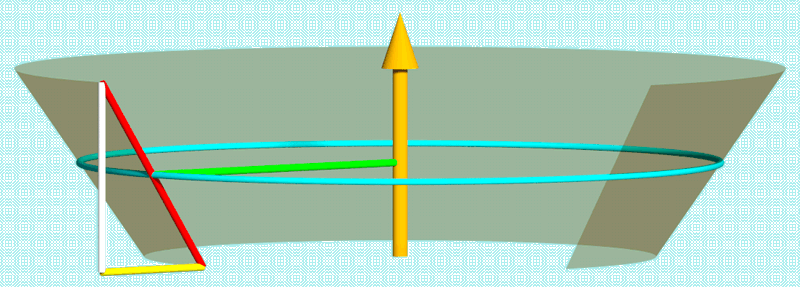
Wie man auf dem folgenden Bild sehen kann ist die Mantelfläche eines Hyperboloids durch eine Anzahl von Abschnitten von Kegelmäntel anzunähern. Bereits drei Stufen für die halbe Höhe ergibt ein passables Erscheinungsbild und die Rechnung dafür lässt sich noch ganz einfach mit dem Taschenrechner durchführen (siehe Tabelle unten).
| Flächenberechnung mit Abschnitten von Kegelmäntel bei 45 Grad | ||||||||
|---|---|---|---|---|---|---|---|---|
| Stufe | Höhe | Radius | mittl. Radius | ΔHöhe | ΔRadius | ΔLänge | Umfang | ΔFläche |
| 0 | 0 | 1 | ||||||
| 1 | 0.4714045 | 1.1055416 | 1.0527708 | 0.4714045 | 0.1055416 | 0.4830748 | 6.614754 | 3.1954209 |
| 2 | 0.942809 | 1.3743685 | 1.2399551 | 0.4714045 | 0.2688269 | 0.5426695 | 7.7908675 | 4.2278659 |
| 3 | 1.4142136 | 1.7320508 | 1.5532097 | 0.4714045 | 0.3576823 | 0.5917422 | 9.7591042 | 5.7748737 |
| verdoppelte Summe der 3 Einzelflächen = Gesamtfläche: | 26.396321 | |||||||
Die Farben in der Tabelle sind mit den Farben im folgenden Bild eines einzelnen stellvertretenden Segments in Übereinstimmung.
Function hyperboloid_flaeche(winkel, strecke, abstand, schritte)
Pi = 4 * Atn(1)
arc = Pi / 180
hoehe = strecke / 2 * Cos(winkel * arc)
x = strecke / 2 * Sin(winkel * arc)
b2 = hoehe * hoehe / ((abstand * abstand + x * x) / abstand * abstand - 1)
delta_hoehe = hoehe / schritte
delta_hoehe2 = delta_hoehe * delta_hoehe
hoehe_alt = 0
radius_alt = abstand
summe = 0
For i = 1 To schritte
hoehe_neu = hoehe_alt + delta_hoehe
radius_neu = abstand * Sqr(1 + hoehe_neu * hoehe_neu / b2)
delta_radius = radius_neu - radius_alt
delta_laenge = Sqr(delta_hoehe2 + delta_radius * delta_radius)
delta_flaeche = (radius_neu + radius_alt) * delta_laenge
summe = summe + delta_flaeche
hoehe_alt = hoehe_neu
radius_alt = radius_neu
Next i
hyperboloid_flaeche = summe * 2 * Pi
End FunctionZum Vergleich ist auch eine Funktion angelegt gemäß dem Ergebnis aus 1.) der strenge Weg zum Ziel.
Function hyperboloid_flaeche1(winkel)
Pi = 4 * Atn(1)
arc = Pi / 180
s = Sin(winkel * arc)
c = Cos(winkel * arc)
w = Sqr(3 * s * s + 1)
hyperboloid_flaeche1 = (2 * Pi * w + Pi * c * c / s * Log((w + 2 * s) / c)) * 2
End FunctionHier folgt ein Beispiel auf einem EXCEL-Tabellenblatt mit einigen Berechnungen der Mantelfläche:
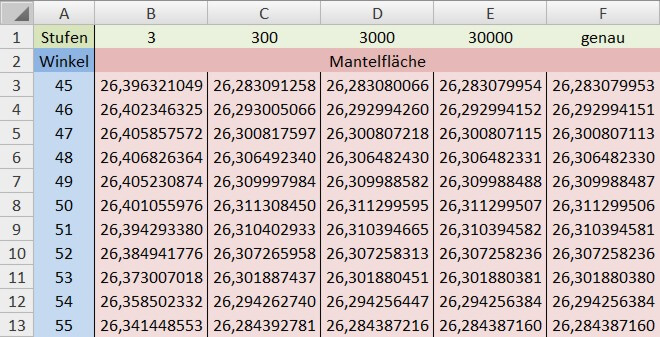
Mit "genau" ist gemeint, dass es keine Stufen gibt und die Genauigkeit nur von der EXCEL-Arithmetik abhängt.
Dabei ist z.B. der Inhalt der Zelle B3: $\quad{\rm =hyperboloid\_flaeche(\$A3;4;1;B\$1)}$
und der Inhalt der Zelle F3: $\quad{\rm =hyperboloid\_flaeche1(\$A3)}$
Mit solchen Tabellen lassen sich leicht die im folgenden mit EXCEL erzeugten Diagramme herstellen.
Da im ersten Teil schon ein Ergebnis berechnet wurde ist es nun interessant, dieses mit den Näherungen bei unterschiedlicher Stufenzahl zu vergleichen. Mit steigender Stufenzahl wird der relative Fehler $(M_{genau}-M_{genähert})/M_{genau}$ immer kleiner, und zwar mit dem Quadrat der Stufenzahl. Bei etwa 100000 Stufen beginnen sich aber die Rundungsfehler spürbar einzustellen und eine Steigerung der Genauigkeit ist durch die in EXCEL wirksame Fließkomma-Arithmetik darüber hinaus nicht mehr möglich.
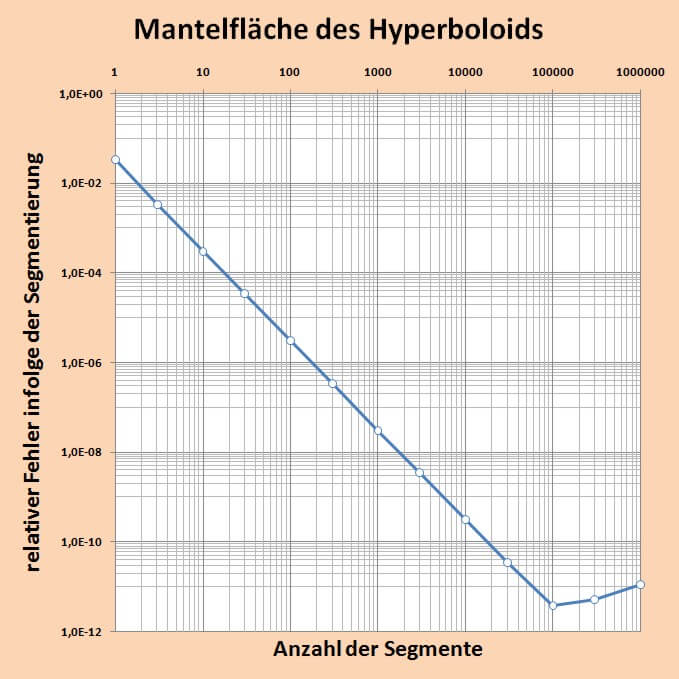
Da nun auf Grund der programmierten Funktion auch die Möglichkeit besteht, mit anderen Verhältnissen als 1:4 Berechnungen durchzuführen, kann man sich schnell einen Überblick über die Kurvenverläufe verschiedener Mantelflächen mit Streckenlängen zwischen 3 und 5 in Abhängigkeit vom Winkel im Bereich 0 bis 90 Grad verschaffen.
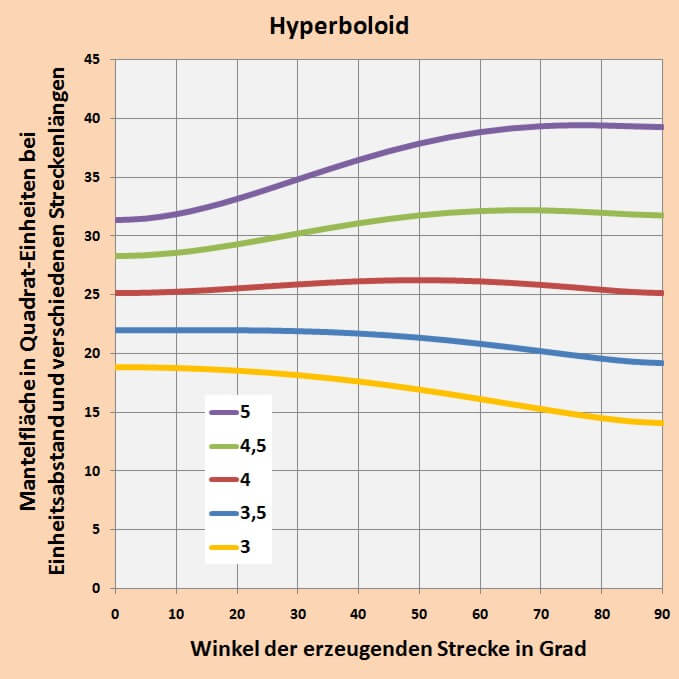
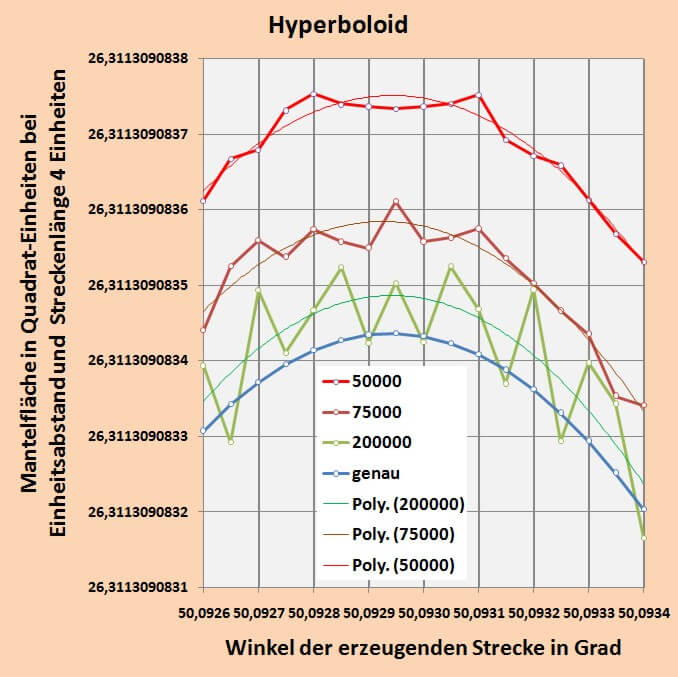
Dabei ist sofort zu erkennen, dass nur bei einem Verhältnis von 1:4 die Mantelfläche am Beginn und am Ende des Winkelbereichs gleich groß ist und etwa in der Mitte ein schwach ausgeprägtes Maximum hat. Ab hier sehen wir uns nur noch den Kurvenverlauf der Mantelfläche mit einem Verhältnis 1:4 an. Im folgenden Diagramm sind 3 Kurvenverläufe mit verschiedener Stufenzahl dargestellt, um zu zeigen, dass eine wenn auch nur geringe Abhängigkeit der Lage des Maximums von der Anzahl der Segmente besteht.
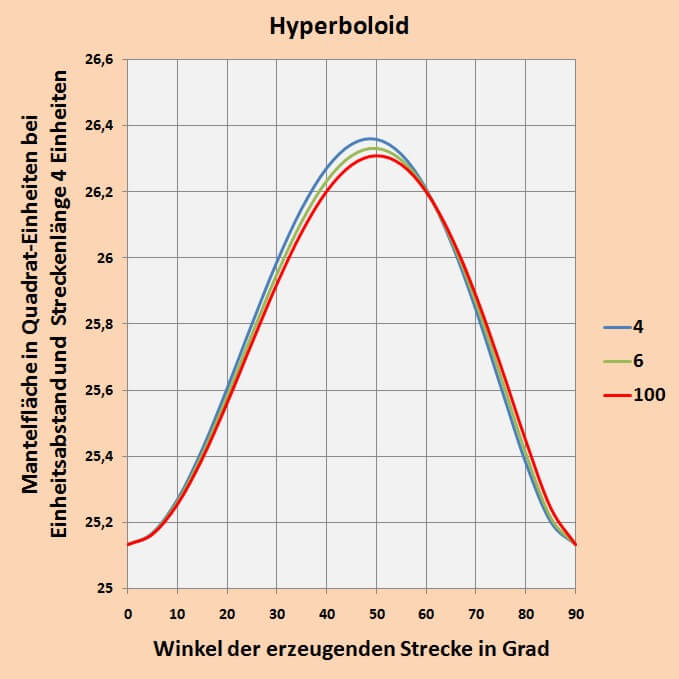
Man erkennt, dass das Maximum sehr nahe bei 50 Grad liegt. Daher ist es sinnvoll, den Bereich um 50 Grad zu spreizen und mit verschiedenen hohen Stufenzahlen ein neues Diagramm zu erzeugen.
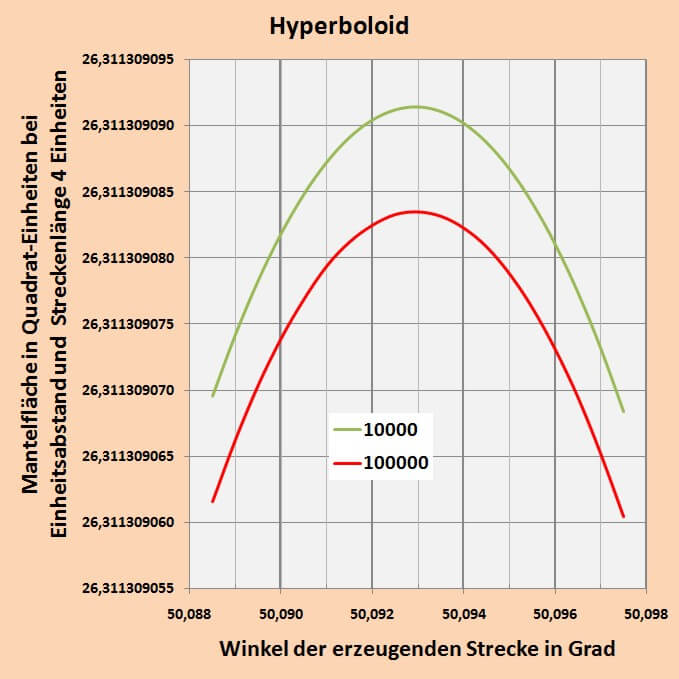
Hier lässt sich nun mit ausreichender Genauigkeit das Maximum der Mantelfläche ablesen: $$\rand{\text{maximale Mantelfläche = 26,31130908 bei einem Winkel von 50,093 Grad}}$$ Eine weitere Steigerung der Auflösung kommt dann an ihre Grenzen, wenn der Kurvenverlauf infolge von Rundungsfehlern nicht mehr glatt erscheint. Hier zeigt sich, wie schon oben bei der Darstellung des relativen Fehlers, dass bei etwa 100000 Stufen EXCEL an eine Grenze kommt. Will man aus welchen Gründen auch immer eine höhere Genauigkeit erzielen so muss mit einer Fließkomma-Arithmetik mit höherer Stellenzahl gerechnet werden.