Lösungsbeschreibung des Preisrätsels vom Januar 2019

Apfelsinen-Kisten

1.) Vorgehensweise

Es ist kaum möglich, durch Probieren schnell die richtige Lösung für dieses Rätsel zu finden. deshalb sollte man nach einigem Probieren systematisch vorgehen.

Das geforderte quaderförmige Volumen hat eine Höhe, Breite und Tiefe, welches mit möglichst ganzzahligen Apfelsinen ausgelegt werden soll. Diese Annahme steht nicht im Widerspruch zu der optimalen hexagonalen besten Kugelpackung, denn auch dann wird durch die Grenzen des Innenraums zwangsweise eine ganzzahlig abzählbare Anzahl der Kugeln entlang der Raumachsen sich ergeben. Es sind auch dann immer gerade Linien von Kugel zu finden, die zumindest einer Achse direkt zuzuordnen sind.

2.) die Zerlegung

Die Zahl 60 lässt sich auf verschiedenste Arten in drei Faktoren für die Raumachsen x, y und z zerlegen. Die Primfaktor-Zerlegung lautet: $$ 60=2\cdot 2\cdot 3\cdot 5 $$ Einige Beispiele für solche Zerlegungen sind:

x	y	z
2	5	6
3	4	5
4	3	5
5	2	6
6	1	10

Es werden zunächst alle möglichen Stapel von Kugel auf ganzzahligen Positionen von karthesischen Gitterpunkten erzeugt. Diese haben dann immer das Kisten-Volumen von 60. Diese noch nicht optimale Packung kann dann durch geeignete Verschiebung von Kugelreihen dichter gepackt werden. Die damit verbundene Verlängerung einer Achse führt aber nicht immer zu eine Abnahme des Gesamtvolumens. Trotzdem ist mit dieser Methode ein minimales Volumen und auch andererseits eine minimale Oberfläche zu finden.

3.) die Verdichtung

Die zuvor beschriebene Verschiebung verringert den Querschnitt des Stapels senkrecht zur Verschiebung. Der ursprüngliche Gitterabstand von $1$ wird auf $\sqrt3/2=0,866$ reduziert aber verlängert gleichzeitig die Achse in Verschiebungs-Richtung um $1/2$. Dabei entstehen auf vier Seiten der Oberfläche hexagonale Muster der Kugeln (siehe unten folgende Animation Bild 1 bis 4).

Im Prinzip ist zusätzlich eine Ebenen-Verschiebung um $\sqrt3/6=0,289$ möglich, um zur besten Kugelpackung zu gelangen, aber auch hier ist der Gewinn an Kompaktheit durch eine Verlängerung der zugehörigen Achse erkauft und wirkt sich erst bei sehr großen Mengen an Kugeln platzsparend aus. Der Gewinn wäre eine Reduzierung des Gitterabstand der Ebenen von $\sqrt3/2=0,866$ auf $\sqrt6/3=0,816$. Dabei ist auch die Wahl der Ebene entscheidend, es gibt zwei Möglichkeiten, davon ist eine in unten folgenden Animation Bild 4 bis 7 zu sehen.

Die Animation zeigt an einem Beispiel, welche Kugelreihen aus dem Stapel(4,3,5) zu verschieben sind, um die beschriebene Verdichtung zu erreichen. Mit einem Klick auf die Bildfläche kann die Animation jederzeit angehalten und wieder gestartet werden.

Bild 1: die Ausgangssituation mit einem unverdichteten Stapel(4,3,5) von 60 Kugeln in einer Kiste
Bild 2: der gleiche unveränderte Stapel ohne Kiste
Bild 3: nach der Verschiebung jeder zweiten 4er-Reihe um 1/2 in x-Richtung
Bild 4: erste Verdichtung der 4er-Reihen in y und z-Richtung von 1 auf 0,866
Bild 5: Verschiebung der mittleren horizontalen xz-Ebene um 0,289 in z-Richtungen
Bild 6: zweite Verdichtung der horizontalen Ebenen in y-Richtung von 0,866 auf 0,816
Bild 7: die gleiche Anordnung wie in Bild 6 aber mit Kiste

Der kleinste Wert für Volumen und Oberfläche ist hier in diesen Beispiel-Stapel allerdings schon nach der ersten Verdichtung erreicht. Die zweite Verdichtung könnte auch alternativ durch Verschieben jeder zweiten xy-Ebene in y-Richtung erfolgen. Dabei wird zwar eine etwas kleinere Oberfläche, aber ein größeres Volumen erzeugt. Auch dabei ist schon nach der ersten Verdichtung das bessere Resultat erreicht.

Die folgenden Tabellen listen alle möglichen Stapelformen mit den Ergebnissen nach der Verdichtung auf. Die erste Tabelle berücksichtigt nur die erste Verdichtung, und darin sind auch die Sieger enthalten. Die zweite und dritte Tabelle zeigt die Ergebnisse nach der zweiten Verdichtung in den beiden möglichen Varianten. Alle Tabellen sind nach Volumen und Oberfläche durch Klick auf die Spaltenüberschrift sortierbar. So kann schnell der beste Wert ermittelt werden.

Die nicht ganzzahligen x-Werte z.B. 7,5 bedeuten, dass abwechselnd in x-Richtung Reihen von 7 und 8 Kugeln angeordnet werden, die bereits gegeneinander verschoben sind. Solche halbzahligen x-Werte sind nur sinnvoll, wenn wenigstens eine der beiden anderen Achszahlen geradzahlig ist, und der doppelte Wert durch die Primfaktoren darstellbar ist, in diesem Beispiel also $2\cdot 7,5=15=3\cdot 5$.

Der Kombi-Wert versucht einen Kompromiss zwischen bestem Volumen-Wert und bestem Oberflächen-Wert zu finden. Er berechnet sich aus dem Mittelwert von Volumen zu bestem Volumen und Oberfläche zu bester Oberfläche: $$ Kombi-Wert=\frac12\cdot \left(\frac{Volumen}{minimales Volumen}+\frac{Oberfläche}{minimale Oberfläche}\right) $$ Die hellgrün hinterlegten Felder sind die minimalen Werte von Volumen, Oberfläche und Kombi-Wert.

Gitterabstand x: 1, y und z: 0,8660254

Anzahl x	Anzahl y	Anzahl z	x Kiste	y Kiste	z Kiste	Volumen Kiste	Oberfläche Kiste	Kombi-Wert Kiste
1	2	30	1,500000	1,866025	26,114737	73,096143	181,403811	1,706952
1	3	20	1,500000	2,732051	17,454483	71,529800	155,932667	1,548513
1	4	15	1,500000	3,598076	13,124356	70,833648	144,612159	1,478096
1	5	12	1,500000	4,464102	10,526279	70,485572	138,951905	1,442888
1	6	10	1,500000	5,330127	8,794229	70,311533	136,121778	1,425283
1.5	1	40	2,000000	1,000000	34,774991	69,549981	212,649944	1,850242
1.5	2	20	2,000000	1,866025	17,454483	65,141016	142,423048	1,412564
1.5	4	10	2,000000	3,598076	8,794229	63,284610	112,853829	1,228279
1.5	5	8	2,000000	4,464102	7,062178	63,052559	109,157677	1,205243
2	1	30	2,500000	1,000000	26,114737	65,286842	187,803157	1,670138
2	2	15	2,500000	1,866025	13,124356	61,225953	123,932667	1,271600
2	3	10	2,500000	2,732051	8,794229	60,065699	105,683956	1,157732
2	5	6	2,500000	4,464102	5,330127	59,485572	96,559600	1,100798
2.5	1	24	3,000000	1,000000	20,918584	62,755753	173,348674	1,564888
2.5	2	12	3,000000	1,866025	10,526279	58,926915	113,638439	1,192005
2.5	3	8	3,000000	2,732051	7,062178	57,882686	97,353829	1,090310
2.5	4	6	3,000000	3,598076	5,330127	57,534610	91,925626	1,056412
3	1	20	3,500000	1,000000	17,454483	61,090689	164,090344	1,497063
3	2	10	3,500000	1,866025	8,794229	57,435889	107,442286	1,143095
3	4	5	3,500000	3,598076	4,464102	56,217622	88,559600	1,025106
4	1	15	4,500000	1,000000	13,124356	59,059600	153,367912	1,417554
4	3	5	4,500000	2,732051	4,464102	54,882686	89,157677	1,016013
5	1	12	5,500000	1,000000	10,526279	57,894537	147,841633	1,375471
5	2	6	5,500000	1,866025	5,330127	54,703838	99,049981	1,070194
5	3	4	5,500000	2,732051	3,598076	54,065699	89,291651	1,009139
6	1	10	6,500000	1,000000	8,794229	57,162486	144,913430	1,352100
6	2	5	6,500000	1,866025	4,464102	54,145826	98,951905	1,064428
7.5	1	8	8,000000	1,000000	7,062178	56,497423	143,119201	1,335758
7.5	2	4	8,000000	1,866025	3,598076	53,712813	100,853829	1,071122
10	1	6	10,500000	1,000000	5,330127	55,966334	143,592921	1,333472
10	2	3	10,500000	1,866025	2,732051	53,529800	106,755753	1,102734
15	1	4	15,500000	1,000000	3,598076	55,770181	149,736515	1,366326
15	2	2	15,500000	1,866025	1,866025	53,971788	122,657677	1,196643
20	1	3	20,500000	1,000000	2,732051	56,007042	158,478185	1,417893
30	1	2	30,500000	1,000000	1,866025	56,913775	178,559600	1,539741

4.) gute Beispiel aus der Liste

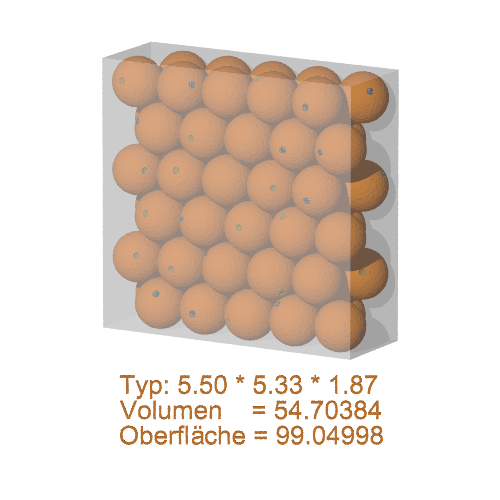
5.) der beste Kombi-Wert

6.) die Gewinner

Die beiden folgenden Listen mit zweifacher Verdichtung bis zur besten Kugelpackung enthalten keine besseren Ergebnisse, sind aber der Vollständigkeit halber aufgelistet.

Gitterabstand x: 1, y: 0,8164966 und z: 0,8660254

Anzahl x	Anzahl y	Anzahl z	Anzahl	x Kiste	y Kiste	z Kiste	Volumen Kiste	Oberfläche Kiste
1	2	30	60	1,500000	1,816497	26,403412	71,942561	180,583140
1	3	20	60	1,500000	2,632993	17,743158	70,076420	154,563679
1	4	15	60	1,500000	3,449490	13,413031	69,402168	143,123786
1	5	12	60	1,500000	4,265986	10,814955	69,204672	137,515719
1	6	10	60	1,500000	5,082483	9,082904	69,245555	134,823566
1.5	1	40	60	2,000000	1,000000	35,063666	70,127332	214,381995
1.5	2	20	60	2,000000	1,816497	17,743158	64,460771	142,699389
1.5	4	10	60	2,000000	3,449490	9,082904	62,662767	112,792341
1.5	5	8	60	2,000000	4,265986	7,350853	62,717276	109,184634
2	1	30	60	2,500000	1,000000	26,403412	66,008530	189,823883
2	2	15	60	2,500000	1,816497	13,413031	60,911811	124,877086
2	3	10	60	2,500000	2,632993	9,082904	59,788059	106,409932
2	5	6	60	2,500000	4,265986	5,618802	59,924333	97,363409
2.5	1	24	60	3,000000	1,000000	21,207259	63,621778	175,658075
2.5	2	12	60	3,000000	1,816497	10,814955	58,935984	115,079363
2.5	3	8	60	3,000000	2,632993	7,350853	58,064237	98,612568
2.5	4	6	60	3,000000	3,449490	5,618802	58,146001	93,173752
3	1	20	60	3,500000	1,000000	17,743158	62,101052	166,688420
3	2	10	60	3,500000	1,816497	9,082904	57,746723	109,293930
3	4	5	60	3,500000	3,449490	4,752777	57,381291	90,205175
4	1	15	60	4,500000	1,000000	13,413031	60,358639	156,543339
4	3	5	60	4,500000	2,632993	4,752777	56,313129	91,499987
5	1	12	60	5,500000	1,000000	10,814955	59,482250	151,594409
5	2	6	60	5,500000	1,816497	5,618802	56,135942	102,201356
5	3	4	60	5,500000	2,632993	3,886751	56,285843	92,184769
6	1	10	60	6,500000	1,000000	9,082904	59,038874	149,243557
6	2	5	60	6,500000	1,816497	4,752777	56,117118	102,667359
7.5	1	8	60	8,000000	1,000000	7,350853	58,806824	148,315353
7.5	2	4	60	8,000000	1,816497	3,886751	56,482164	105,372508
10	1	6	60	10,500000	1,000000	5,618802	58,997423	150,232450
10	2	3	60	10,500000	1,816497	3,020726	57,614953	112,555950
15	1	4	60	15,500000	1,000000	3,886751	60,244646	159,262794
15	2	2	60	15,500000	1,816497	2,154701	60,667095	130,935123
20	1	3	60	20,500000	1,000000	3,020726	61,924882	170,891216
30	1	2	60	30,500000	1,000000	2,154701	65,718366	196,746134

Gitterabstand x: 1, y: 0,8660254 und z: 0,8164966

Anzahl x	Anzahl y	Anzahl z	Anzahl	x Kiste	y Kiste	z Kiste	Volumen Kiste	Oberfläche Kiste
1	2	30	60	1,500000	2,154701	24,678401	79,761845	186,848431
1	3	20	60	1,500000	3,020726	16,513435	74,823842	158,367606
1	4	15	60	1,500000	3,886751	12,430952	72,474030	145,585150
1	5	12	60	1,500000	4,752777	9,981462	71,159494	139,082042
1	6	10	60	1,500000	5,618802	8,348469	70,362595	135,718608
1.5	1	40	60	2,000000	1,288675	32,843367	84,648860	221,177027
1.5	2	20	60	2,000000	2,154701	16,513435	71,163015	145,835557
1.5	4	10	60	2,000000	3,886751	8,348469	64,896848	113,837730
1.5	5	8	60	2,000000	4,752777	6,715476	63,834317	109,707328
2	1	30	60	2,500000	1,288675	24,678401	79,506104	193,440263
2	2	15	60	2,500000	2,154701	12,430952	66,962448	126,498222
2	3	10	60	2,500000	3,020726	8,348469	63,046094	107,282851
2	5	6	60	2,500000	4,752777	5,082483	60,389766	97,488111
2.5	1	24	60	3,000000	1,288675	19,779421	76,467745	177,387076
2.5	2	12	60	3,000000	2,154701	9,981462	64,521187	115,831102
2.5	3	8	60	3,000000	3,020726	6,715476	60,856838	98,988438
2.5	4	6	60	3,000000	3,886751	5,082483	59,263042	93,324100
3	1	20	60	3,500000	1,288675	16,513435	74,481586	167,175677
3	2	10	60	3,500000	2,154701	8,348469	62,959579	109,499091
3	4	5	60	3,500000	3,886751	4,265986	58,032898	90,230820
4	1	15	60	4,500000	1,288675	12,430952	72,087565	155,515563
4	3	5	60	4,500000	3,020726	4,265986	57,988690	91,353162
5	1	12	60	5,500000	1,288675	9,981462	70,745743	149,697238
5	2	6	60	5,500000	2,154701	5,082483	60,231758	101,511475
5	3	4	60	5,500000	3,020726	3,449490	57,309797	92,012299
6	1	10	60	6,500000	1,288675	8,348469	69,930021	146,799806
6	2	5	60	6,500000	2,154701	4,265986	59,747500	101,852775
7.5	1	8	60	8,000000	1,288675	6,715476	69,232536	145,374553
7.5	2	4	60	8,000000	2,154701	3,449490	59,460939	104,532279
10	1	6	60	10,500000	1,288675	5,082483	68,771528	146,893658
10	2	3	60	10,500000	2,154701	2,632993	59,569774	111,888191
15	1	4	60	15,500000	1,288675	3,449490	68,901711	155,773655
15	2	2	60	15,500000	2,154701	1,816497	60,667095	130,935123
20	1	3	60	20,500000	1,288675	2,632993	69,557993	167,574546
30	1	2	60	30,500000	1,288675	1,816497	71,396656	194,097223

Diese Informationen wurden zusammengestellt von