Lösungsbeschreibung des Preisrätsels vom Juli 2016

1.) der Vergleich: Ikosaederstumpf mit Fußball

Der Fußball ist ein "aufgeblasener" Ikosaederstumpf.

Wenn man die Flächen durchzählt findet man 20 weiße Sechsecke und 12 schwarze Fünfecke. Es sind aber nur beim Ikosaederstumpf ebene Flächen, beim Fußball sind es Teile einer Kugeloberfläche. Die Eckpunkte sind aber bei beiden Körpern an gleicher räumlicher Position, beim Ikosaederstumpf auf der Oberfläche der Umkugel, die der Fußball-Oberfläche entspricht. Die immer gleich langen geraden Kanten beim Ikosaederstumpf werden beim Fußball zu etwas längeren aber auch immer gleich langen Bogenabschnitten von Großkreisen.

2.) Berechnung der Flächen beim Ikosaederstumpf

Es ist sinnvoll, sich auf eine Länge als Einheit festzulegen und das ist die immer gleiche Kantenlänge beim Ikosaederstumpf. Sie wird im Weiteren mit $a$ bezeichnet. Man könnte sie auch gleich zu $1$ machen, aber es ist vielleicht besser, wenn man bei Flächen immer noch die Dimension am auftretenden $a^2$ erkennen kann.

Die Flächen der ebenen Fünf- und Sechsecke sind nun leicht (notfalls mit Hilfe von Wikipedia) anzugeben: $$\sand{\begin{align} F_{ebenes\;Fünfeck}&=\frac54\cdot\sqrt{1+\frac2{\sqrt5}}\cdot a^2=1,72047740\cdot a^2 \\ F_{ebenes\;Sechseck}&=\frac32\cdot\sqrt3\cdot a^2=2,59807621\cdot a^2 \end{align}}$$ Die gesamte Oberfläche des Ikosaederstumpfes ist dann $$\sand{ O_{Ikosaederstumpf}=12\cdot F_{ebenes\;Fünfeck}+20\cdot F_{ebenes\;Sechseck}=72,60725303\cdot a^2 }$$ Das Verhältnis von weißen zu schwarzen Flächen ist damit $$\sand{ \frac{F_{weiß}}{F_{schwarz}}=\frac{20\cdot F_{ebenes\;Sechseck}}{12\cdot F_{ebenes\;Fünfeck}}=2,51681714}$$ Für weiter unten folgende Berechnungen ist noch der Umkugelradius von nutzen, denn alle Eckpunkte, auch die des Fußballs, liegen auf dieser Kugel: $$\sand{ r_{Umkugel}=\frac a4\cdot\sqrt{58+18\sqrt{5}}=2,47801866\cdot a }$$

3.) Berechnung der Flächen beim Fußball

Die Oberfläche des Fußballs kann sofort angegeben werden: $$\sand{ O_{Fußball}=4\cdot \pi r_{Umkugel}^2=77,16475977\cdot a^2 }$$ Die nicht flachen Polygone beim Fußball sind etwas schwieriger zu berechnen. Die Vorgehensweise wird im folgenden Bild für das Kugelsechseck gezeigt. Entsprechendes gilt aber auch für das Kugelfünfeck. Alle Winkelangaben sind im folgenden im Bogenmaß angegeben und werden auch so in den Formeln benutzt. Zusätzlich wird eine Umrechnung in Grad angezeigt.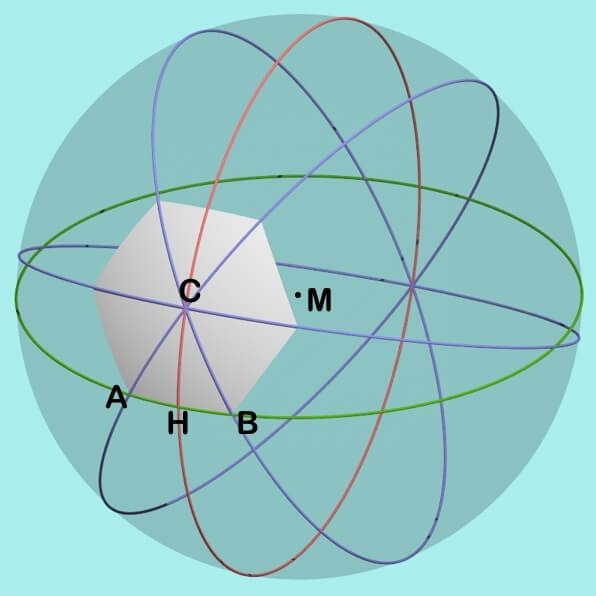

Die Berechnung der Sechseckfläche erfolgt durch Zerteilen in 12 gleiche Kugeldreiecke von der Größe $\triangle AHC$. Darin ist der Winkel bei Punkt $C$: $$\sand{ \frac{\gamma}2=\frac{2\pi}{12}=0,52359878=30,00000000° }$$ und der Winkel bei $H$ ist ein rechter. Darüber hinaus lässt sich die Bogenlänge $\overparen{AH}$ als die Hälfte des Bogens $\overparen{AB}$ erkennen. Dieser ist der Bogen über der Strecke $\overline{AB}$, die durch die Kugel geradlinig hindurch geht und die Länge $a$ hat. Die Länge des Bogens $\overparen{AB}$ ist $$\sand{ \overparen{AB}=2\pi\cdot r_{Umkugel}\cdot\frac{\delta}{2\pi}=r_{Umkugel}\cdot\delta }$$ mit dem Winkel $\delta$ im Dreieck $\triangle ABM$ am Punkt $M$, dem Mittelpunkt der Kugel.
In diesem Dreieck sind alle drei Seiten bekannt und daraus berechnet sich nach dem Cosinussatz für ebene Dreiecke $$\sand{ \delta=\arccos{\frac{a^2-2r_{Umkugel}^2}{-2r_{Umkugel}^2}}=\arccos\left(1-\frac{a^2}{2r_{Umkugel}^2}\right) = 0,40633789 = 23,28144627° }$$ und $$\sand{ \overparen{AB}=\arccos\left(1-\frac{a^2}{2r_{Umkugel}^2}\right)\cdot r_{Umkugel} = 1,00691288\cdot a }$$ Nun zum sphärischen rechtwinkligen Dreieck $\triangle AHC$. Es gilt hier wie für alle sphärischen Dreiecke der Sinussatz: $$\sand{ \frac {\sin(\alpha)} {\sin\left( \frac {\overparen{HC}} {r_{Umkugel}}\right)}= \frac {\sin(\pi/2 )} {\sin\left( \frac {\overparen{AC}} {r_{Umkugel}}\right)}= \frac {\sin(\gamma/2)} {\sin\left( \frac {\overparen{AH}} {r_{Umkugel}}\right)} }$$ wobei alle Streckenbögen auf eine Einheitskugel normiert werden müssen, also man muss sie durch $r_{Umkugel}$ teilen.
$\pi/2$ ist der rechte Winkel. Es kann nun $\overparen{AC}$ berechnet werden. $$\sand{ \overparen{AC}=\overparen{BC}=r_{Umkugel}\cdot\arcsin\left(\frac{\sin\left(\frac12\cdot\frac{\overparen{AB}}{r_{Umkugel}}\right)}{\sin\left(\frac{\gamma}2\right)}\right)=1,02934801\cdot a \\ }$$ Der Sinussatz für das sphärische Dreieck $\triangle ABC$ lautet: $$\sand{ \frac {\sin(\alpha)} {\sin\left( \frac {\overparen{BC}} {r_{Umkugel}}\right)}= \frac {\sin(\beta )} {\sin\left( \frac {\overparen{AC}} {r_{Umkugel}}\right)}= \frac {\sin(\gamma)} {\sin\left( \frac {\overparen{AB}} {r_{Umkugel}}\right)} }$$ Es kann nun $\alpha$ berechnet werden. $$\sand{ \alpha=\beta=\arcsin\left(\frac{\sin\left(\frac{\overparen{BC}}{r_{Umkugel}}\right)\cdot \sin(\gamma)}{\sin\left(\frac{\overparen{AB}}{r_{Umkugel}}\right)}\right)= 1,08480382 = 62,15468023° }$$ Jetzt kann die Fläche des sphärischen Sechsecks berechnet werden: $$\sand{ F_{sphärisches\;Sechseck}=6\cdot(\alpha+\beta+\gamma-\pi)\cdot r_{Umkugel}^2 = 2,77108971\cdot a^2 }$$ Nur durch Veränderung von $\gamma=\frac{2\pi}{6}$ auf $\gamma=\frac{2\pi}{5}$ (damit ändert sich auch $\alpha$) und der Vervielfachung von 6 auf 5 ergibt sich die Formel für das sphärische Fünfeck: $$\sand{ F_{sphärisches\;Fünfseck}=5\cdot(\alpha+\beta+\gamma-\pi)\cdot r_{Umkugel}^2 = 1,81191380\cdot a^2 }$$ Zunächst der Test auf Richtigkeit: $$\sand{ O_{Fußball}=12\cdot F_{sphärisches\;Fünfeck}+20\cdot F_{sphärisches\;Sechseck}=77,16475977\cdot a^2 }$$ Der Wert für die Oberfläche der gesamten Fußball-Kugel stimmt genau mit der obigen Rechnung mit dem Umkugel-Radius überein. Zum Abschluss nun die entscheidende Frage: Wie lautet des Verhältnis von weiß zu schwarz: $$\rand{ \frac{F_{weiß}}{F_{schwarz}}=\frac{20\cdot F_{sphärisches\;Sechseck}}{12\cdot F_{sphärisches\;Fünfeck}}=2,54895285}$$

4.) Zusammenstellung

Körpereigenschaft	Ikosaederstumpf	Fußball	%-Zuwachs
Kantenlänge [a]	1,00000000	1,00691288	0,69128785
Fläche Fünfeck [a²]	1,72047740	1,81191380	5,31459456
Fläche Sechseck [a²]	2,59807621	2,77108971	6,65929263
Oberfläche [a²]	72,60725303	77,16475977	6,27693039
Volumen [a³]	55,28773076	63,73857151	15,28520096
Verhältnis weiß : schwarz	2,51681714	2,54895285	1,27683924

Diese Informationen wurden zusammengestellt von


Kurzbewertung dieser Information:
sehr gut	gut	befriedigend
ausreichend	mangelhaft	ungenügend