Lösungsbeschreibung des Preisrätsels vom Februar 2016

1.) Endlicher Automat

Ein endlicher Automat (auch Zustandsmaschine, Zustandsautomat; englisch finite state machine (FSM)) ist ein Modell eines Verhaltens, bestehend aus Zuständen, Zustandsübergängen und Aktionen. Ein Automat heißt endlich, wenn die Menge der Zustände, die er annehmen kann endlich ist. Ein Zustand speichert die Information über die Vergangenheit, d.h., er reflektiert in gewissem Umfang die Änderungen der Eingabe seit dem Systemstart (RESET) bis zum aktuellen Zeitpunkt. Ein Zustandsübergang wird durch logische Bedingungen beschrieben, die erfüllt sein müssen, um den Übergang zu ermöglichen. Eine Aktion ist die Ausgabe des endlichen Automats, die in einer bestimmten Situation erfolgt.

Beispiel: der Automat (Blackbox) befindet sich im Zustand $s$ und es wird ein Eingang $t$ (Taste) aktiv. Dann wechselt der Automat gemäß seiner Programmierung für die noch unbekannte aber zu bestimmende logische Bedingung $f(s,t)$ in einen neuen Zustand. Wir nehmen für $s$ hier den Anfangszustand $s_0=$

an und betätigen die Taste 1. Der Automat wechselt in den neuen Zustand

, von dem wir noch nicht wissen, wie wir ihn bezeichnen sollen. Man kann zunächst nicht sicher sein, dass eine eineindeutige (wechselseitige) Beziehung zwischen Zustand und Anzeige besteht. Das wird sich bei der weiteren Untersuchung hoffentlich aufklären lassen.

2.) Spielen mit den Tasten

Um einen Überblick über die Eingänge (Tasten) und Ausgänge (Lampen) zu bekommen ist es sinnvoll, die Tasten einzeln solange wiederholt zu betätigen, bis ein Schema erkennbar wird. Hier folgt eine Tabelle, die in drei Spalten separat die aufeinander folgenden Anzeigen für jede Taste auflistet. Die Nr. gibt die Anzahl der Tasten-Aktivierungen wieder.

Nr.	Taste 1	Taste 2	Taste 3
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

Tabelle 1

3.) Schlussfolgerungen

Nach jeweils 64 Auslösungen derselben Taste beginnt eine Wiederholung der Abfolge. Die Abfolgen der 3 Tasten sind verschieden, enthalten aber die gleichen Elemente in anderer Anordnung. Die Anzeige der drei Lampen zeigen verschiedene Kombinationen von Farben (schwarz, rot, gelb, grün), insgesamt auch 4³ = 64 Kombinationen.

Bleibt man nicht bei einer Taste, kann man weitere Zusammenhänge finden.
Beispiel: Tastenfolge RESET, Taste 1, Taste 2, Taste 3 führt zu den folgenden Anzeigen:

RESET
Taste 1
Taste 2
Taste 3

Tabelle 2

Wenn man nun versucht, aus der Tabelle 1 das Verhalten abzulesen dann gelingt das leicht: Der Übergang von

nach

ist genau das Verhalten am Anfang der Spalte Taste 1. Sucht man nun in Spalte Taste 2 nach dem Zustand

, so findet man ihn in Zeile 39. Das Auslösen der Taste 2 führt dann zum darunter befindlichen Zustand

in Zeile 40. Sucht man in der Spalte Taste 3 nach

so findet man das in Zeile 8. Der darunter befindliche Zustand

erscheint nach dem Drücken der Taste 3.
Wenn man nach dem RESET die Reihenfolge der Tasten verändert, z.B. Taste 3, Taste 2, Taste 1 so ergibt sich:

RESET
Taste 3
Taste 2
Taste 1

Tabelle 3

Man kommt also zum gleichen Endzustand, nur die Zwischenwerte sind verschieden, aber mit der Tabelle 1 nachvollziehbar. Die Blackbox verhält sich in Bezug auf die Tastenreihenfolge kommutativ. Wenn man sich das Tasten als Schreiten mit unterschiedlicher Schrittlänge für jede Taste vorstellt, dann wird dasselbe Ziel mit jeder Reihenfolge erreicht, nur die Zwischenstopps sind an unterschiedlicher Stelle.

Schlussfolgerungen:

1.)	die Blackbox hat mindestens 2⁶=64 innere Zustände, die durch jeweils eine eindeutige farbige Anzeige der drei Lampen erkennbar werden.
2.)	die Abfolge von Tastenauslösungen ist kommutativ.
3.)	die Tasten wirken nicht auf den Ablauf anderer Tasten ein, soweit man das mit relativ kleinen Zahlen von Tastenauslösungen beurteilen kann.
4.)	jede Taste hat eine eigene unveränderliche Schrittweite. Das kann man an weiteren Beispielen ähnlich wie in Tabelle 2 und Tabelle 3 nachprüfen.
5.)	die Schrittweiten für alle drei Tasten sind ungeradzahlig, weil ansonsten die Periode kleiner als 64 wäre, man wäre schon nach spätestens 32 Schritten wieder am Ausgangspunkt.
6.)	der angestrebte Zustand wird gemäß Tabelle 1 mit Taste 1 nach 59 Schritten erreicht, Taste 2 benötigt 61 Schritte und Taste 3 kommt mit 49 Schritte aus. Alle sind ungeradzahlig. Deshalb muss die Zielweite von = Zustandsnummer = Schrittzahl mal Schrittweite auch ungeradzahlig sein. Nur ungeradzahlige Anzahlen von Tastungen können den Zielzustand erreichen.

4.) Berechnungen

Die unterschiedlichen Schrittweiten der 3 Tasten und die Zuordnung von Weglängen zu den Zuständen sind noch unbekannt. Aber es gibt Beziehungen zwischen den Tasten, wie aus Tabelle 1 abzulesen ist. Man kann z.B. die Taste 1 durch dreimal Taste 3 ersetzen.

	Taste 1	Taste 2	Taste 3
Taste 1 =	1x	39x	3x
Taste 2 =	23x	1x	5x
Taste 3 =	43x	13x	1x

Tabelle 4

Es ist, wie sich später zeigt, für die Beantwortung der ersten Rätselfrage nicht von Bedeutung mit welcher ungeraden Zahl als Entfernung vom Anfangszustand man einen Zustand belegt. Wenn man also den Zielzustand

willkürlich festlegt, z.B. auf die Zahl 59, dann ergeben sich daraus die Schrittweiten für die drei Taste:

Taste	Schrittzahl	Schrittweite	Zielnummer = 59
1	59	1	(59*1) mod 64 = 59
2	61	23	(61*23) mod 64 = 59
3	49	43	(49*43) mod 64 = 59

Tabelle 5

Die Zahl 59 habe ich gewählt, weil dann die Schrittweite für Taste 1 sich natürlich zu 1 ergibt. Zur Berechnung der Schrittweiten der beiden anderen Tasten kann ein keines EXCEL-Programm genutzt werden:


Function Schrittweite(Schrittzahl, Zielnummer)
Grenze = 0
Do
Schrittweite = (Grenze * 64 + Zielnummer) / Schrittzahl
Grenze = Grenze + 1
Loop Until Schrittweite = Int(Schrittweite) Or Grenze = 64
If Grenze = 64 Then Schrittweite = "???"
End Function

Jetzt kann die erste Frage des Rätsels angegangen werden. Es sind die Schrittweiten der 3 Tasten bekannt, wenn das Ziel als 59 definiert wird. $$(t_1\cdot 1+t_2\cdot 23+t_3\cdot 43)\bmod 64=59$$ Die Parameter $t_1$, $t_2$ und $t_3$ kann man sich als die Stellen eines 3-stelligen Zählwerks vorstellen, die jeweils die Werte 0 bis 18 durchlaufen können. 18 ist der Maximalwert, denn nur Lösungen mit weniger als 20 Tastenauslösungen sind gesucht und mindestens 2 Tasten sind an einer Lösung beteiligt, weil die Schrittzahl zum Zielzustand mit einer Taste gemäß Tabelle 1 mindestens 49 ist. Bei jeder Stellung des Zählwerks wird geprüft, ob die obige Gleichung erfüllt ist. Wenn ja, ist das eine Lösung. Wenn nein, wird zusätzlich geprüft, ob die Summe von $t_1$, $t_2$ und $t_3$ größer als 19 ist. Dann wird $t3$ auf 18 gestellt und anschließend das Zählwerk einen Schritt weiter getaktet. Wenn $t_1$ größer als 18 wird ist die Suche nach Lösungen beendet. Man kann das von Hand machen, aber ein kleines Programm erledigt das hier in der folgenden Tabelle:

lfd. Nr	t₁	t₂	t₃	Summe	Varianten
1	0	8	9	17	24310
2	0	9	4	13	715
3	1	7	11	19	604656
4	1	8	6	15	45045
5	1	9	1	11	110
6	2	7	8	17	875160
7	2	8	3	13	12870
8	3	6	10	19	7759752
9	3	7	5	15	360360
10	3	8	0	11	165
11	4	6	7	17	4084080
12	4	7	2	13	25740
13	5	5	9	19	23279256
14	5	6	4	15	630630
15	6	5	6	17	5717712
16	6	6	1	13	12012
17	7	4	8	19	24942060
18	7	5	3	15	360360
19	8	4	5	17	3063060
20	8	5	0	13	1287
21	9	3	7	19	11085360
22	9	4	2	15	75075
23	10	3	4	17	680680
24	11	2	6	19	2116296
25	11	3	1	15	5460
26	12	2	3	17	61880
27	13	1	5	19	162792
28	13	2	0	15	105
29	14	1	2	17	2040
30	15	0	4	19	3876
31	16	0	1	17	17

Tabelle 6

Es gibt also 31 verschiedene Grundlösungen mit weniger als 20 Tastungen. Die kürzesten mit 11 Tastungen sind in Zeile 5 und 10 grün markiert. Jede einzelne Lösung kann in vielen Varianten auftreten, denn die Reihenfolge ist beliebig.
Deshalb gibt es für jede der obigen Grundlösungen $$\left(\matrix{ t_1+t_2+t_3 \cr t_1,t_2,t_3 }\right)=\frac{(t_1+t_2+t_3)!}{t_1!\cdot t_2!\cdot t_3!}\text{ Varianten }\href{https://de.wikipedia.org/wiki/Multinomialkoeffizient}{\text{ (Permutation mit Wiederholung)}}$$ Insgesamt gibt es mit maximal 19 Tastungen $$ 85992921\text{ Lösungen}$$ Damit ist die Frage 1 des Rätsels ausreichen beantwortet.

5.) Modellvorstellung

Nach dem bisher herausgefundenen ist der zentrale Kern der Blackbox ein 6-Bit Binärzähler mit 2⁶ = 64 Zuständen, der durch die Auslösung der 3 verschiedenen Tasten unterschiedlich weit vorangezählt wird. Die Taste RESET setzt den Zähler auf Null zurück. Der jeweilige Zählerstand wird durch eine eindeutige Farbkombination der drei Lampen angezeigt. Wenn man mit der obigen Festlegung des Zielzustands

auf den Zahlenwert $59 = 111011$ eine Methode zur Ausgabe sucht, wird es schwierig. Man benötigt einen aufwändigen Dekodierer, der zu jedem Zustand eine eigene Ausgabenkombination für die Lampen generiert. Schöner wäre, wenn jede Lampe mit 2 Bits des Binärzählers so angesteuert werden könnte, dass das eine Bit eine rote LED und das andere Bit eine grüne LED jeweils beim Zustand $1$ aufleuchten ließe. Sind beide Bits auf $1$ entsteht die Mischfarbe gelb. Das ist aber mit 59 nicht möglich weil nur 5 von 6 Bits gesetzt sind. Man kann durch einen Inverter bei Bit 3 aus der 59 eine 63 machen aber für den Zustand

mit $35 = 100011$ und den Zustand

mit $24 = 011000$ müsste diese Korrektur ebenfalls zu einer richtigen Anzahl von Bits führen, was nicht der Fall ist.

Deshalb definiere ich den Zustand

neu auf den Zahlenwert 63 und erhalte für die Schrittweiten der drei Tasten die neuen Werte:

Taste	Schrittzahl	Schrittweite	Zielnummer = 63
1	59	13	(59*13) mod 64 = 63
2	61	43	(61*43) mod 64 = 63
3	49	47	(49*47) mod 64 = 63

Tabelle 7

Die neue Zählung ergibt sich aus der alten Zählung indem mit der neuen Schrittweite der Taste 1, die zuvor den Wert 1 hatte, multipliziert wird. Dasselbe gilt für die jeweilige Schrittweite der 3 Tasten: $$\text{neue Zählung}=\text{(alte Zählung}\cdot 13)\bmod 64\\ \text{neue Schrittweite}=\text{(alte Schrittweite}\cdot 13)\bmod 64$$ Aus der folgenden Tabelle erkennt man den Erfolg der neuen Nummerierung. Man kann die Bits den einzelnen LEDs perfekt zuordnen.

alte Zählung	Anzeige	neue Zählung
59 = 111011		63 = 111111
35 = 100011		7 = 000111
24 = 011000		56 = 111000
5 = 000101		1 = 000001
10 = 001010		2 = 000010
20 = 010100		4 = 000100
32 = 100000		32 = 100000
16 = 010000		16 = 010000
40 = 101000		8 = 001000
37 = 100101		33 = 100001
26 = 011010		18 = 010010
60 = 111100		12 = 001100

Tabelle 8

Nun ist das einfachste Modell einer Blackbox mit den gegebenen Eigenschaften zu erstellen. Ein Nachbau wäre so möglich. Damit ist die Frage 2 des Rätsels beantwortet.

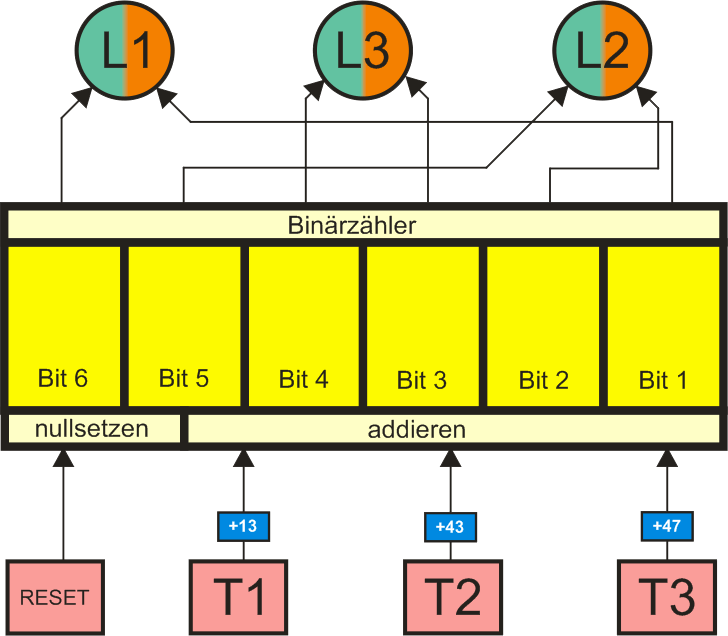6.) abstraktes Modell

Bis hierher ist die Modellvorstellung angelehnt an die mechanischen Schrittschaltwerke, wie sie bei Ablaufsteuerungen z.B. in Waschmaschinen in der Vorcomputerzeit üblich waren. Mit Beginn des Microprozessors und seiner Programmierbarkeit kam eine neue Methode auf: die Steuerung mit Hilfe einer Übergangstabelle. Darin sind alle Zustände und die Bedingungen für den Übergang in einen neuen Zustand zeilenweise aufgelistet. Die Zustände können mit Namen oder Nummern oder Symbole (Lampenfarben) gekennzeichnet werden und den verschiedenen Eingängen (Tasten) sind Sprungziele zum nächsten Zustand zugeordnet. Nur aus Gründen der Vollständigkeit ist auch die RESET-Taste dabei.

Nr. = binär	Taste 1	Taste 2	Taste 3
0 = 000000	19	54	55
1 = 000001	24	55	60
2 = 000010	25	60	61
3 = 000011	26	61	62
4 = 000100	23	51	56
5 = 000101	28	56	57
6 = 000110	29	57	58
7 = 000111	30	58	59
8 = 001000	27	62	63
9 = 001001	48	63	20
10 = 001010	49	20	21
11 = 001011	50	21	22
12 = 001100	31	59	16
13 = 001101	52	16	17
14 = 001110	53	17	18
15 = 001111	54	18	19
16 = 010000	7	35	40
17 = 010001	12	40	41
18 = 010010	13	41	42
19 = 010011	14	42	43
20 = 010100	8	39	44
21 = 010101	9	44	45
22 = 010110	10	45	46
23 = 010111	11	46	47
24 = 011000	15	43	0
25 = 011001	36	0	1
26 = 011010	37	1	2
27 = 011011	38	2	3
28 = 011100	32	47	4
29 = 011101	33	4	5
30 = 011110	34	5	6
31 = 011111	35	6	7
32 = 100000	51	22	23
33 = 100001	56	23	28
34 = 100010	57	28	29
35 = 100011	58	29	30
36 = 100100	55	19	24
37 = 100101	60	24	25
38 = 100110	61	25	26
39 = 100111	62	26	27
40 = 101000	59	30	31
41 = 101001	16	31	52
42 = 101010	17	52	53
43 = 101011	18	53	54
44 = 101100	63	27	48
45 = 101101	20	48	49
46 = 101110	21	49	50
47 = 101111	22	50	51
48 = 110000	39	3	8
49 = 110001	44	8	9
50 = 110010	45	9	10
51 = 110011	46	10	11
52 = 110100	40	7	12
53 = 110101	41	12	13
54 = 110110	42	13	14
55 = 110111	43	14	15
56 = 111000	47	11	32
57 = 111001	4	32	33
58 = 111010	5	33	34
59 = 111011	6	34	35
60 = 111100	0	15	36
61 = 111101	1	36	37
62 = 111110	2	37	38
63 = 111111	3	38	39

Tabelle 9

Die Einträge für die Tasten in der obigen Tabelle scheinen willkürlich zu sein, aber natürlich steckt ein System darin. Das ist auch nicht weiter verwunderlich, weil ja immer noch die gleiche Blackbox vorliegt wie unter Punkt 5 in der Modellvorstellung beschrieben. Nur die Bits sind umsortiert, um eine direkte Zuordnung ohne Auskreuzungen zu den Ausgangs-LEDs zu ermöglichen. Die Zahlen (Sprungziele) der Tasten 1 bis 3 sind mit einer recht einfachen Formel zu berechnen: $$s_{n+1}=f(s_n,t_i)=\trans(\itrans(s_n)+t_i)$$ Dabei ist $s_{n+1}$ die Nummer des Sprungziels, also des Zielzustands nach dem Drücken einer der Tasten 1 bis 3, wenn vom Zustand $s_n$ gestartet wird. Der Wert von $t_i$ hängt von der Tasten-Nummer $i$ ab. $$t_1 =13\\ t_2 =43\\ t_3 =47$$ Die Funktionen $\trans()$ und $\itrans()$ tauschen nur die untersten 6 Bits der im Binärcode dargestellten Zahlenwerte. Überträge in höhere Bits werden nicht berücksichtigt.

	6	5	4	3	2	1
⇑ itrans() ⇑	Zähler-Bits						⇓ trans() ⇓
	⇕	⇕	⇕	⇕	⇕	⇕
	6	4	2	1	3	5
	Ziel-Bits

$trans()$ ist die Umkehrfunktion von $itrans()$. Daraus folgt: $$\trans(\itrans(s_n))=\itrans(\trans(s_n))=s_n\quad\text{für}\quad 0 \le s_n < 2^6$$ Die Funktionen sind sehr einfach aufgebaut. Hier sind sie in der Programmiersprache PHP gelistet:


function itrans($nr)
{
  $sum = 0;
  $g = array(4,8,2,16,1,32);
  for ($i = 0; $i < 6; $i++)
  {
    $sum += $g[$i]*($nr % 2);
    $nr >>= 1;
  }
  return $sum;
}


function trans($nr)
{
  $sum = 0;
  $g = array(16,4,1,2,8,32);
  for ($i = 0; $i < 6; $i++)
  {
    $sum += $g[$i]*($nr % 2);
    $nr >>= 1;
  }
  return $sum;
}

Zum Abschluss noch ein Berechnungsbeispiel: im Zustand Nr. 10 wird die Taste 1 gedrückt und es ergibt sich 49.

	---> Taste 1 --->
10 = 001010			49 = 110001
itrans:			trans:
24 = 011000		+ 13 =	37 = 100101

Sollte irgendwann mal die Frage aufkommen, aus welchem Zustand ist man mit einer bestimmten Taste zum gegenwärtigen Zustand gelangt, so ist die Antwort darauf mit einem Vorzeichenwechsel von $t_i$ leicht auf die gleiche Weise wie oben zu berechnen. Statt aber tatsächlich für die "Rückwärtsfuntion" der Taste 1 den Wert $-13$ zu nehmen ist es besser $64-13=51$ zu wählen, denn damit ist sicher gestellt, dass keine negativen Werte in die Berechnung eingehen.


Kurzbewertung dieser Information:
sehr gut	gut	befriedigend
ausreichend	mangelhaft	ungenügend

Nr.	Taste 1	Taste 2	Taste 3
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

Nr.	Taste 1	Taste 2	Taste 3
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64