Preisrätsel: Lösungen 2014

Lösungen anderer Jahre:
2008	2009	2010	2011	2012	2013	2014	2015	2016	2017	2018	2019	2020

Lösung des Preisrätsels vom Dezember 2014:

Weihnachtsstern

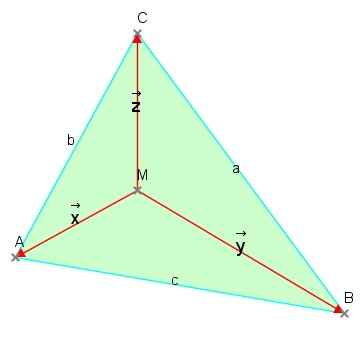
a)	$d = 2 \cdot (r_{Innenkugel\;des\;Ikosaeders} + h_{Pyramide})$ $d = 2\left(\frac{a}{12}\sqrt3(3+\sqrt5) + a\sqrt{\frac{11}3}\right)\\ = \rand{5,341231a}$
b)	$\Delta d=Kante_{Dodekaeder}\\ \text{ mit}\; d_{Außenkugel}=d\;\text{aus a)}$ $\frac{\Delta d}2\sqrt3(\sqrt5+1)=2\left(\frac{a}{12}\sqrt3(3+\sqrt5) + a\sqrt{\frac{11}3}\right)$ $\Delta d=\frac a{12}(\sqrt5-1)(3+\sqrt{5}+4\sqrt{11})\\ = \rand{1,905869a}$

nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom November 2014:

Einsame Erde

	jul. Datum	Kalenderdatum	Winkel
a)	2460383,15	13.03.2024 15:36:00	121,1
b)	2525826,97	19.05.2203 11:09:36	135,3
c)	2698158,29	16.03.2675 18:57:36	147,7

Klick auf ein Kalenderdatum zeigt das Sonnensystem zum jeweiligen Datum maßstabsgerecht. Mit dem Mauszeiger auf dem schwarzen Hintergrund kann man mit dem Mausrad den Zoomfaktor verändern.

nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom Oktober 2014:

Dreieck einmal anders

a)	$x=\frac37\\y=\frac47\\z=\frac57$	$\Longrightarrow$	$a=\frac17\cdot\sqrt{61}\\b=1\\c=\frac17\cdot\sqrt{37}$
b)	$a=\frac37\\b=\frac47\\c=\frac57$	$\Longrightarrow$	$x=0,484074521047723\\y=0,336286156939902\\z=0,146272545944133$
c)	Ja, es gibt solche Ausdrücke, aber einfach sind sie nicht. siehe: Ausführliche Beschreibung der Lösung

nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom September 2014:

Astronomische Uhr am Rathaus in Oslo

Im Rathaushof zur Stadtseite zeigt die astronomische Uhr aus dem Jahre 1931 die Zeit, das Datum, den Sonnenstand im Tierkreis (Zodiac) und die Mondphasen an. Eine zusätzliche Besonderheit ist der Drachenzeiger, der die Position der Mondknoten kennzeichnet. Eine Sonnen- oder eine Mondfinsternis findet nur statt, wenn sich Sonne und Mond gemeinsam auf dem Drachenzeiger treffen. Der Kopf des Drachenzeigers zeigt dabei die Position des aufsteigenden Knotens im Tierkreis.

Das Bild wurde aufgenommen am 11. Juli 2013 gegen 14 Uhr Sommerzeit.
Der Mondzeiger lässt aber auf den 9. Juli schließen (14° statt 40° zur Sonne).

nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom August 2014:

Ausflug in höhere Dimensionen

$P_{4,1}=0,500000$	$P_{4,2}=0,288675$	$P_{4,3}=\\0,204124$	$P_{4,4}=\\0,790569$
$Z_{4,1}=0,500000$	$Z_{4,2}=0,288675$	$Z_{4,3}=\\0,204124$	$Z_{4,4}=\\0,158114$
$P_{k,i}=\displaystyle{\frac1{\sqrt{2i\cdot(i+1)}}}\quad\text{für }i\lt k\quad\text{und}\quad P_{k,k}=\displaystyle{\frac{k+1}{\sqrt{2k\cdot(k+1)}}}$
$Z_{k,i}=\displaystyle{\frac1{\sqrt{2i\cdot(i+1)}}}$
$\varphi_3=109,471221°$	$\varphi_4=104,477512°$	$\varphi_k=\\ \arccos(-1/k)\cdot180°/\pi $
$d_3=0,612372$	$d_4=0,632456$	$d_k=\displaystyle{\frac{k}{\sqrt{2k\cdot(k+1)}}}$

nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom Juli 2014:

Nr	$\matrix{3\cr 4}$ <---------------------------> $\matrix{0\cr 1}$	S
1	0001010110101001101110110111111001	20
2	0111010010111001011001100111100011	19
3	0111011110111001001001100011011001	19
4	0101111111111111111110110001010101	25
5	1101011010101011101111110111100110	23
6	1111111000110001001001100011110011	19

links: Nummer der Teilsumme
mitte: Binärdarstellung der beteiligten Summanden
rechts: Anzahl der Summanden

Teilsumme
Es gibt 6 mögliche Teilsummen (siehe Tabelle links).
Das jeweils niederwertigste Bit der Binärdarstellung rechts entspricht dem ersten Summanden, also Rechnung Nr. 1, eine 1 bedeutet dass der jeweilige Summand Bestandteil der Teilsumme ist, ansonsten 0.
In allen 6 Teilsummen kommt 7, 12, 16, 19, 24, 29 und 31 vor. Diese (grün) sind sicher enthalten.
Der Summand 10 kommt nicht vor. Dieser (rot) ist sicher nicht enthalten.

Ausführliche Beschreibung der Lösung
nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom Juni 2014:
	Standfuß für Glaskugel Das Volumenverhältnis von Kugel zu Standfuß ist 24,276747602147 Ausführliche Beschreibung der Lösung nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom Mai 2014:
	Netzwerk Der resultierende Gesamtwiderstand zwischen den Kontaktpunkten A und Null ist gleich dem Wert eines der 21 gleichen Einzelwiderstände. Die Spannungen am Punkt B ist 31/56 der Spannung zwischen A und Null. Die Spannungen am Punkt C ist 53/112 der Spannung zwischen A und Null. Ausführliche Beschreibung der Lösung nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom April 2014:

Raumsonden

Rosetta	New Horizons	Cassini
Voyager	Pioneer 10	STEREO
MAVEN	DAWN	Spitzer

nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom März 2014:

Satelliten-Flachantenne
Die Satelliten-Flachantenne ist eine noch nicht weit verbreitete Alternative zur Sat-Schüssel. Das Signal z.B. von geostationären Fernseh-Satelliten wird nicht mit einem Parabolspiegel gebündelt und dann im Brennpunkt mit einem LNB (Low Noise Block) aufgenommen, sondern mit 128 Empfängern (16 horizontal x 8 vertikal) phasenrichtig aufsummiert und dann auf die gleiche Weise wie in einem LNB weiterverarbeitet, also verstärkt und zum Weiterleiten über ein Koax-Kabel in eine Zwischenfrequenz umgesetzt.
Abmessungen: 288 mm x 535 mm x 70 mm
Gewicht: 3,5 kg
Antennengewinn: 32,5 dB
nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom Februar 2014:

Blackbox
Die Tasten T1 bis T4 wirken auf die Eingänge der beiden Zähler ZL und ZR. Zusätzlich bewirken die Tasten T2 und T3 ein Zurücksetzen des jeweils anderen Zählers und sollten deshalb nicht benutzt werden. Die Lampen L1 bis L4 zeigen den Zustand der niederwertigen Bits der Zähler an. Wenn beide Zähler den Wert 011 haben werden beide Zähler zurückgesetzt. Diese Zählerstellung ist zu vermeiden, indem einer der beiden über diesen Wert hochgezählt wird, bevor der andere 011 erreicht. Ein Aufleuchten aller Lampen ist bei den Zählerstellungen 011 111 und 111 011 und 111 111 erreicht, also bei 3 von insgesamt 2⁶=64 inneren Zuständen. Die kürzeste erfolgreiche Tastenabfolge hat demnach eine Länge von 10 = 7+3.
Hier zwei von 1920 Möglichkeiten:
4 4 4 4 4 4 4 1 1 1 oder 1 1 1 1 1 1 1 4 4 4
nochmal zurück zu diesem Rätsel

Lösung des Preisrätsels vom Januar 2014:
	Mantelfläche des Hyperboloids Das Maximum der Mantelfläche des Hyperboloids ist bei 50,093 Grad. Ausführliche Beschreibung der Lösung nochmal zurück zu diesem Rätsel

Lösungen anderer Jahre:
2008	2009	2010	2011	2012	2013	2014	2015	2016	2017	2018	2019	2020