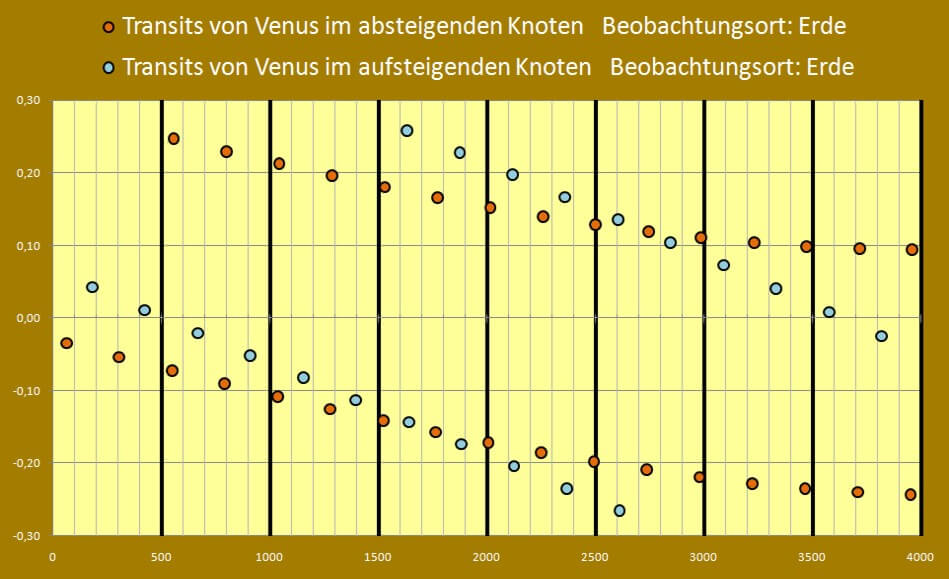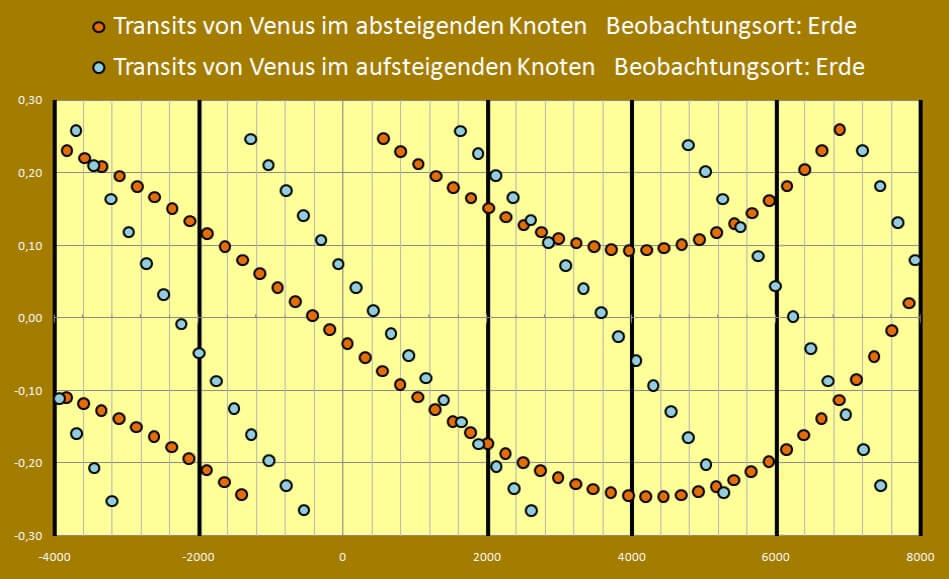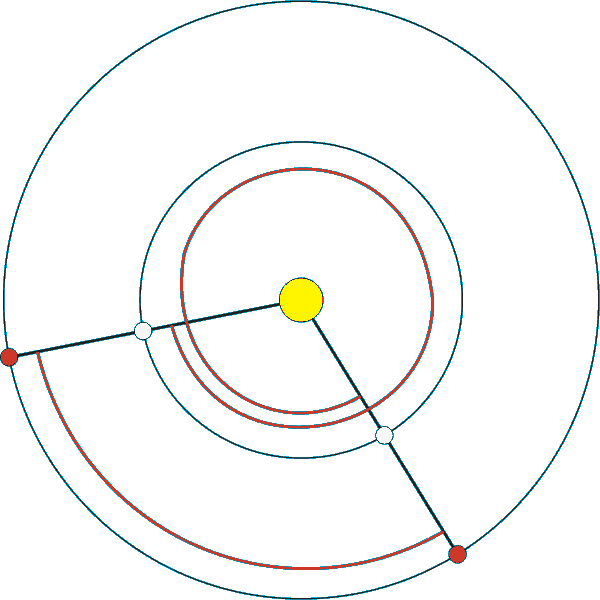

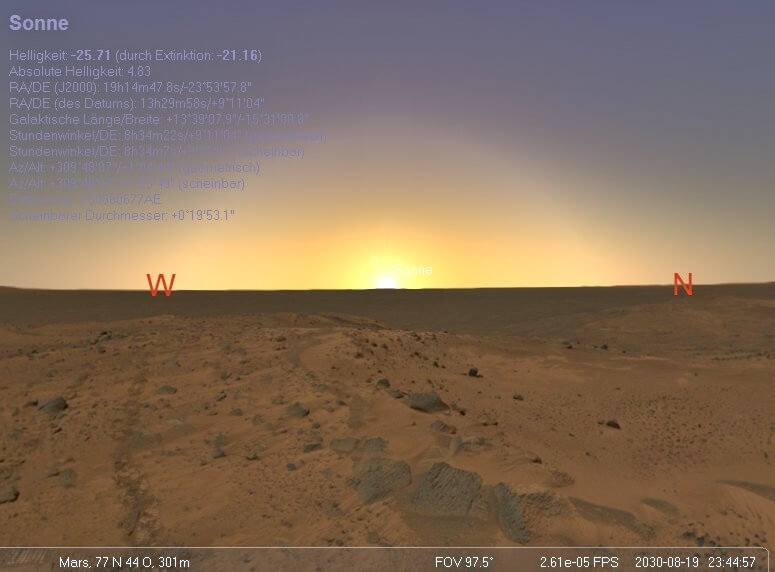

| Venustransits aus Sicht des Mars | |||
|---|---|---|---|
| tsyn=333,922 Tage | |||
| Datum | Uhrzeit in UTC | nächster Transit | tsyn |
| 19. August 2030 | 23:44:57 | 1,8311 | 2 |
| 18. Juni 2032 | 18:53:33 | 27,3794 | 30 |
| 5. November 2059 | 03:03:45 | 4,6174 | 5 |
| 17. Juni 2064 | 15:34:21 | 27,3822 | 30 |
| 5. November 2091 | 00:09:45 | 4,6146 | 5 |
| 16. Juni 2096 | 11:23:42 | 1,8310 | 2 |
| 16. März 2098 | 05:57:29 | 27,3787 | 30 |
| 2. September 2125 | 07:18:52 | 4,6183 | 5 |
| 16. April 2130 | 02:54:16 | 27,3814 | 30 |
| 2. September 2157 | 03:53:38 | 4,6155 | 5 |
| 14. April 2162 | 22:58:23 | 1,8309 | 2 |
| 12. Februar 2164 | 16:56:30 | 27,3779 | 30 |
| Venustransits aus Sicht der Erde | |||
|---|---|---|---|
| tsyn=583,924 Tage | |||
| Datum | Uhrzeit in UTC | nächster Transit | tsyn |
| 6. Juni 1761 | 05:12:50 | 7,9937 | 5 |
| 3. Juni 1769 | 22:23:54 | 105,5119 | 66 |
| 9. Dezember 1874 | 03:56:42 | 7,9933 | 5 |
| 6. Dezember 1882 | 17:01:37 | 121,5021 | 76 |
| 8. Juni 2004 | 08:22:12 | 7,9937 | 5 |
| 6. Juni 2012 | 01:31:39 | 105,5114 | 66 |
| 11. Dezember 2117 | 02:51:18 | 7,9933 | 5 |
| 8. Dezember 2125 | 15:58:33 | 121,5025 | 76 |
| 11.Juni 2247 | 11:29:08 | 7,9937 | 5 |
| 9. Juni 2255 | 04:36:49 | 105,5110 | 66 |
| 13. Dezember 2360 | 01:49:08 | 7,9933 | 5 |
| 10. Dezember 2368 | 14:58:57 | 121,5030 | 76 |
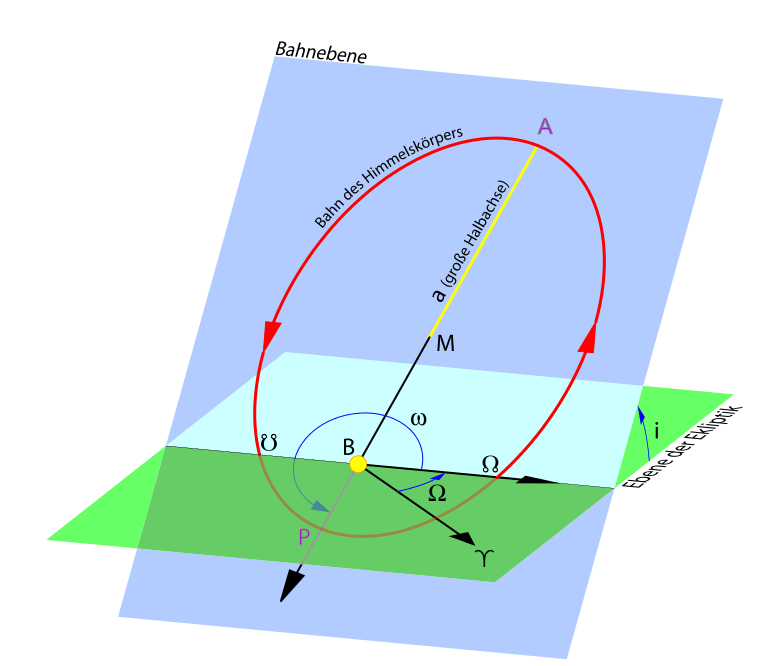
| Bahnelemente | |
|---|---|
| a | große Halbachse der Ellipse |
| e | Exzentrizität: Form der Ellipse |
| i | Inklination: Neigungswinkel der Bahnebene gegen die Ekliptik |
| Ω | Winkel vom Frühlingspunkt ♈ zum aufsteigenden Knoten ☊ |
| ω | Winkel vom aufsteigenden Knoten zum Perihel |
| M | Mittlere Anomalie |
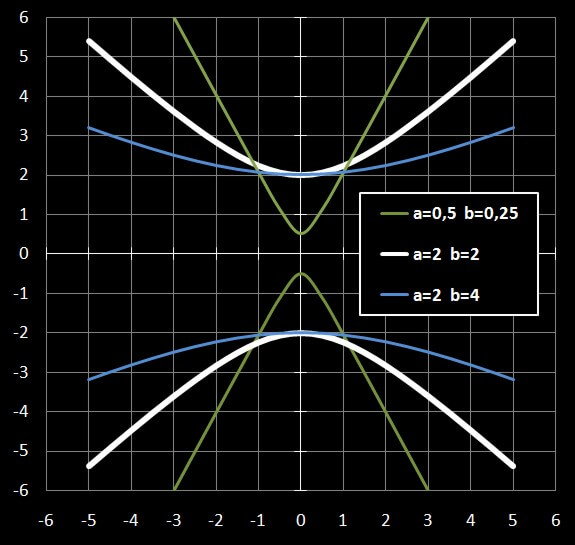
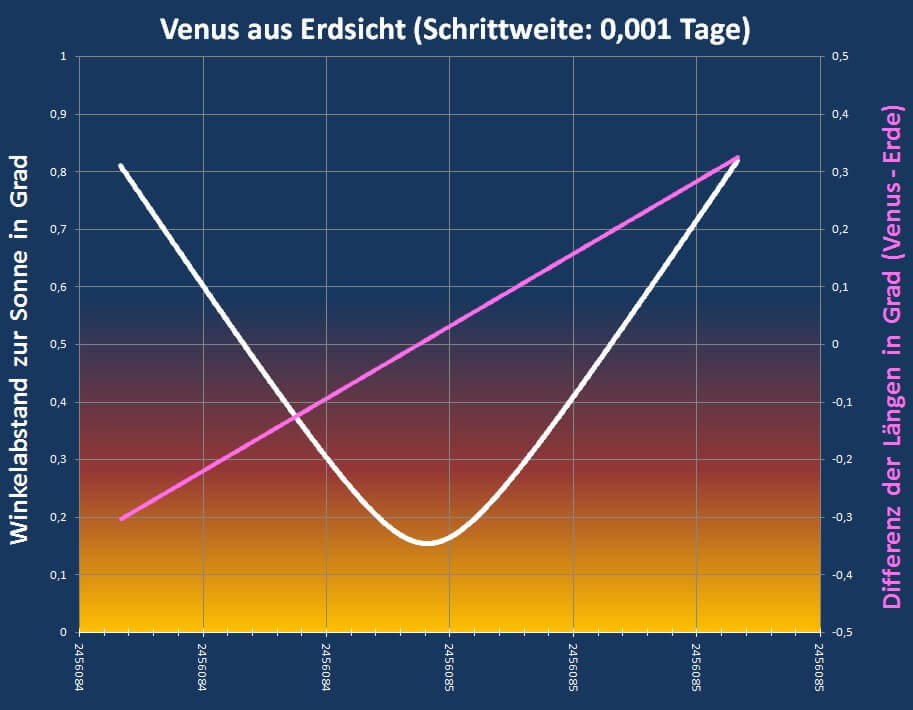
 $$ \text{y wird zur Distanz d:}\quad\sand{y = d} $$
$$ \text{x wird zur Zeit t:}\quad\sand{x = t} $$
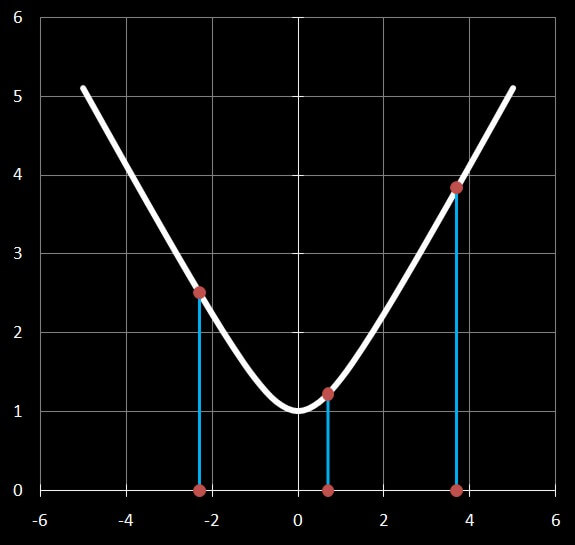
Bekannt sind drei Werte der Distanz $d_1$, $d_2$ und $d_3$ mit den zugehörigen Zeiten
$$ \sand{t_1 = t-i}\quad\sand{t_2 = t}\quad\sand{t_3 = t+i} $$
und damit die drei Gleichungen
$$ \sand{\left(\frac{d_1}a\right)^2 = 1+\left(\frac{t-i}b\right)^2} \tag{5a} $$
$$ \sand{\left(\frac{d_2}a\right)^2 = 1+\left(\frac tb\right)^2} \tag{5b} $$
$$ \sand{\left(\frac{d_3}a\right)^2 = 1+\left(\frac{t+i}b\right)^2} \tag{5c} $$
mit den Unbekannten $a$, $b$ und $t$, wobei vorzugsweise $t$ interessiert, die noch zu kompensierende Zeit bis zum Minimum.
$$ \text{y wird zur Distanz d:}\quad\sand{y = d} $$
$$ \text{x wird zur Zeit t:}\quad\sand{x = t} $$
Bekannt sind drei Werte der Distanz $d_1$, $d_2$ und $d_3$ mit den zugehörigen Zeiten
$$ \sand{t_1 = t-i}\quad\sand{t_2 = t}\quad\sand{t_3 = t+i} $$
und damit die drei Gleichungen
$$ \sand{\left(\frac{d_1}a\right)^2 = 1+\left(\frac{t-i}b\right)^2} \tag{5a} $$
$$ \sand{\left(\frac{d_2}a\right)^2 = 1+\left(\frac tb\right)^2} \tag{5b} $$
$$ \sand{\left(\frac{d_3}a\right)^2 = 1+\left(\frac{t+i}b\right)^2} \tag{5c} $$
mit den Unbekannten $a$, $b$ und $t$, wobei vorzugsweise $t$ interessiert, die noch zu kompensierende Zeit bis zum Minimum.