Lösungsbeschreibung des Preisrätsels vom November 2018

Skulptur

1.) der Schnittkörper

Der Schnittkörper ist eine dreiseitige regelmäßige Pyramide mit Kanten, die an der unten liegenden Spitze im rechten Winkel aufeinander treffen. Wenn die Größe des gleichseitigen Basisdreiecks bekannt ist, sind auch die übrigen Abmessungen der Pyramide leicht zu berechnen.

Die Forderung nach maximaler Eindringtiefe ist die Frage nach dem größten Dreieck auf der Deckfläche des unteren Würfels. Dabei ist aber zusätzlich zu beachten, dass die Mitte des Dreiecks genau auf der Mitte des Quadrats liegen muss. Das ergibt sich aus der Festlegung der senkrechten Raumdiagonale und der Lage der Würfelmittelpunkte genau übereinander.

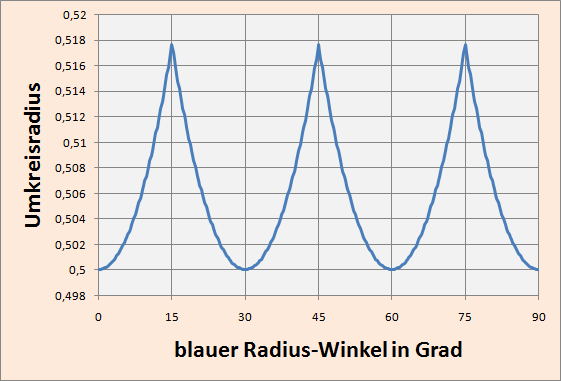
Die folgende animierte Grafik zeigt den Bereich der Möglichkeiten für das maximale Dreieck. Daneben den Funktionverlauf des Umkreisradius in Abhängigkeit vom Winkel gegen die Horizontale. Aus der gegebenen Kantenlänge $a=1,0\;m$ des Würfels sind die folgenden Größen zu berechnen:

• $d$ = Raumdiagonale im Würfel
• $r$ = maximaler Radius des Umkreises der Dreiecks-Grundfläche der Pyramide
• $s$ = Seitenlänge der Dreiecks-Grundfläche
• $k_p$ = Kantenlänge der Pyramide (eine der unteren Ecke zur Spitze)
• $h_p$ = Höhe der Pyramide
• $G_p$ = Grundfläche der Pyramide
• $S_p$ = einzelne Seitenfläche der Pyramide
• $O_p$ = Oberfläche der Pyramide
• $V_p$ = Volumen der Pyramide

$$ d=\sqrt{a^2+a^2+a^2}=\sqrt{3}\cdot a=1,732050807569\;m \\ r=\frac{a}{2\cdot \cos{15°}}=\frac{2a}{\sqrt{6}+\sqrt{2}}=0,517638090205\;m \\ s=\frac{2r}{\cos{30°}}=\frac{2a\cdot\sqrt{3}}{\sqrt{6}+\sqrt{2}}=0,896575472168\;m \\ k_p=\frac{s\cdot\sqrt{2}}{2}=\frac{a\cdot\sqrt{6}}{\sqrt{6}+\sqrt{2}}=0,633974596216\;m \\ h_p=\sqrt{{k_p}^2-r^2}=\frac{a}{\sqrt{3}+1}=0,366025403784\;m \\ G_p=\frac{s}2\cdot\sqrt{s^2-\frac{s^2}4}=\frac{s^2}4\cdot\sqrt{3}=0,348076211353\;m^2 \\ S_p=\frac{{k_p}^2}2=\frac{3a^2}4\cdot(2-\sqrt{3})=0,200961894323\;m^2 \\ O_p=3\cdot S_p + G_p=0,950961894323\;m^2 \\ V_p=\frac13 G_p\cdot h_p=0,042468245269\;m^3 \\ $$

2.) die Beantwortung der Rätselfragen 1 bis 3

Mit der Kantenlänge der Würfel mit $a=1,000000000000\;m$ ergibt sich: $$\rand{\begin{align} \text{Höhe der Skulptur} &= a+d-h_p=2,366025403784\;m \\ \text{Volumen der Skulptur} &= a^3+a^3-V_p=1,957531754731\;m^3 \\ \text{Oberfläche der Skulptur} &= 11\cdot a^2-O_p=10,049038105677\;m^2 \end{align}}$$

3.) die Berechnung der Schwerpunkthöhe

Der Mittelpunkt des oberen Würfels ist genau eine Kantenlänge über dem Mittelpunkt des unteren Würfels: $$ \text{Abstand der Mittelpunkte} = \frac{a}2+\frac{d}2-h_p=1,000000000000\;m $$ Das bedeutet, dass der obere Würfel auf den unteren gestapelt wird und dann nur noch in die richtige Position um den Mittelpunkt gedreht werden muss.
Wenn man zunächst davon absieht, dass die beiden Würfel die oben berechnete Schnittpyramide gemeinsam haben, dann ist in erster Näherung der Schwerpunkt auf der Hälfte der Strecke zwischen den Mittelpunkten, also in einer Höhe $s≈1,0\;m$. Tatsächlich ist aber die genaue Berechnung etwas komplizierter. Man muss von einem der Würfel die Schnittpyramide abziehen und den dadurch veränderten Schwerpunkt für diesen Restkörper berechnen. Da die Skulptur aus einem einheitlichen Material besteht, kann statt der Masse auch mit den Volumina gerechnet werden.

Die folgenden Größen werden zur Berechnung benutzt:

• $V_r$ = Volumen des Restkörpers (unterer Würfel minus Pyramide)
• $s_r$ = Schwerpunkthöhe des Restkörpers über der Grundfläche der Skulptur
• $V_p$ = Volumen der Pyramide = 0,042468245269$\;m^3$
• $s_p$ = Schwerpunkthöhe der Pyramide über der Grundfläche der Skulptur
• $V_o$ = Volumen des oberen Würfels = 1,000000000000$\;m^3$
• $s_o$ = Schwerpunkthöhe des oberen Würfels über der Grundfläche der Skulptur
• $V_u$ = Volumen des unteren Würfels = 1,000000000000$\;m^3$
• $s_u$ = Schwerpunkthöhe des unteren Würfels über seiner Grundfläche
• $V$ = Volumen der Skulptur = 1,957531754731$\;m^3$
• $s$ = gesuchte Schwerpunkthöhe über der Grundfläche der Skulptur

$$ V_u=V_r+V_p \\ V_r=V_u-V_p=0,957531754731\;m^3 $$ Damit sind alle Volumina bekannt. Nun müssen die Höhen der Schwerpunkte bestimmt werden, immer gemessen ab der Bodenfläche der Skulptur: $$ s_p=a-\frac{h_p}{4}=0,908493649054\;m \\ s_o=\frac12a+a=1,500000000000\;m \\ s_u=\frac12a=0,500000000000\;m $$ Es fehlt noch die Schwerpunkthöhe des Restkörpers. Dazu muss die folgende Gleichung nach $s_r$ aufgelöst werden: $$ V_r \cdot (s_u-s_r)= V_p \cdot (s_p-s_u) \\ s_r=s_u-\frac{V_p}{V_r}\cdot(s_p-s_u)=0,481882576329\;m $$ Zuletzt ist noch die folgende Gleichung nach $s$ aufzulösen: $$ V_r \cdot (s-s_r)= V_o \cdot (s_o-s) \\ V_r \cdot s+V_o \cdot s=V_o \cdot s_o+V_r \cdot s_r \\ (V_r+V_o)\cdot s=V_o \cdot s_o+V_r \cdot s_r \\ \rand{s=\frac{V_o \cdot s_o+V_r \cdot s_r}{V_r+V_o}=1,001985211298\;m} $$ Wie sich zeigt, war die oben versuchte Abschätzung schon recht gut.

Es kommt übrigens das gleiche Ergebnis heraus, wenn der Restkörper aus dem oberen Würfel entwickelt wird: $$ V_r \cdot (s_r-s_o)= V_p \cdot (s_o-s_p) \\ s_r=s_o+\frac{V_p}{V_r}\cdot(s_o-s_p)=1,526234364204\;m $$ Und nun noch die neue Berechnung von $s$: $$ V_r \cdot (s_r-s)= V_u \cdot (s-s_u) \\ V_r \cdot s+V_u \cdot s=V_u \cdot s_u+V_r \cdot s_r \\ (V_r+V_u)\cdot s=V_u \cdot s_u+V_r \cdot s_r \\ \rand{s=\frac{V_u \cdot s_u+V_r \cdot s_r}{V_r+V_u}=1,001985211298\;m} $$ Es gibt eben nur einen Schwerpunkt, unabhängig vom Rechenweg!

Diese Informationen wurden zusammengestellt von