1.) die Krümmung von Mondbahnen
Der Erdmond läuft auf einer Ellipse um den gemeinsamen Schwerpunkt von Erde und Mond, und dieser umkreist die Sonne auch auf einer Ellipse. Beide sind gegeneinander um etwas mehr als 5 Grad geneigt. Die hier zu berechnenden Mondbahnen sind aber idealisiert, weil statt der Ellipsen nur Kreise angenommen werden sollen, und diese liegen zudem in einer Ebene.Die Funktionsgleichung von solchen vereinfachten Mondbahnen sind Epitrochoiden und die Parameterdarstellung ist $$\overrightarrow{z}(t)=\overrightarrow{p}(t)+\overrightarrow{m}(t)=\pmatrix{x(t)\cr y(t)} =\pmatrix{r_p\cdot\cos(\omega_p\cdot t)+r_m\cdot\cos(\omega_m\cdot t) \cr r_p\cdot\sin(\omega_p\cdot t)+r_m\cdot\sin(\omega_m\cdot t)}\tag{1}$$ $$\text{mit Winkelgeschwindigkeit }\quad \omega_p=\frac{2\pi}{T_p} \quad \text{und} \quad \omega_m=\frac{2\pi}{T_m}\quad (\;_p ≙ \text{Planet,}\;_m ≙ \text{Mond)}$$ $$\begin{align} r_p & = \text{Planetenbahn-Radius} \\ r_m & = \text{Mondbahn-Radius} \\ T_p & = \text{Planeten-Umlaufzeit} \\ T_m & = \text{Mond-Umlaufzeit} \end{align}$$ Zur Berechnung der Krümmung einer ebenen Funktion ist folgende Formel zu verwenden (Herleitung): $$\kappa(t)=\frac {x'(t)\cdot y''(t)-x''(t)\cdot y'(t)} {\Big( x'(t)^{2}+y'(t)^{2}\Big)^\frac32}\tag{2}$$ Die vier erforderlichen Ableitungen sind $$\begin{align} x'(t) & = -r_p\omega_p\cdot\sin(\omega_p\cdot t)-r_m\omega_m\cdot\sin(\omega_m\cdot t) \\ x''(t) & = -r_p\omega_p^2\cdot\cos(\omega_p\cdot t)-r_m\omega_m^2\cdot\cos(\omega_m\cdot t) \\ y'(t) & = +r_p\omega_p\cdot\cos(\omega_p\cdot t)+r_m\omega_m\cdot\cos(\omega_m\cdot t) \\ y''(t) & = -r_p\omega_p^2\cdot\sin(\omega_p\cdot t)-r_m\omega_m^2\cdot\sin(\omega_m\cdot t) \end{align}$$ Eingesetzt in (2) und vereinfacht ergibt $$\kappa(t)=\frac { \omega_m^3 r_m^2 + \omega_p^3 r_p^2 + \omega_m \omega_p r_m r_p\cdot(\omega_m + \omega_p)\cdot \cos((\omega_m - \omega_p) t) } { \Big(\omega_m^2 r_m^2 + \omega_p^2 r_p^2 + 2\omega_m \omega_p r_m r_p\cdot \cos((\omega_m - \omega_p) t)\Big)^\frac32 }\tag{3}$$ mit der Bahngeschwindigkeit $v_p=\frac{2\pi r_p}{T_p}=\omega_p r_p$ und $v_m=\frac{2\pi r_m}{T_m}=\omega_m r_m$ ergibt sich eine etwas kompaktere Darstellung $$\kappa(t)=\frac { \omega_m v_m^2 + \omega_p v_P^2 + v_m v_p\cdot(\omega_m + \omega_p)\cdot \cos((\omega_m - \omega_p) t) } { \Big(v_m^2 + v_p^2 + 2v_m v_p \cdot \cos((\omega_m - \omega_p) t)\Big)^\frac32 }\tag{4}$$ Damit ist der größte Teil der Arbeit für dieses Rätsel getan.
2.) Analyse der Krümmungsformel
Wenn man den Aufbau der Formel schematisch darstellt so ergibt sich $$\kappa(t)=\frac { A+B\cdot\cos(C\cdot t) }{\Big(b^2+c^2+2bc\cdot\cos(C\cdot t)\Big)^\frac32 }\tag{5}$$ Der Zähler ist also eine reine Cosinus-Schwingung mit Amplitude B und Frequenz C, angehoben um den Gleichanteil A.Der Nenner ist größer oder gleich Null, wie man an der folgenden Grafik sieht:
Kosinussatz:$$a^2=b^2+c^2-2bc\cdot\cos(\alpha)$$ $$(a')^2=(b')^2+c^2+2b'c\cdot\cos(\alpha)$$ |
Die gelbe Seite des Dreiecks entspricht dann bis auf die Potenz dem Nenner. Das unterschiedliche Vorzeichen beim Cosinus-Term lässt sich anders als beim Dreieck durch eine negative Geschwindigkeit erklären, oder mit einer Phasenverschiebung des Arguments vom Cosinus um 180°, was auf das gleiche hinausläuft und in der Grafik durch die gestrichenen Elemente dargestellt wird. Wenn man die Geschwindigkeiten vektoriell benutzt, geht der Cosinus-Term in den Vektorpfeil über und man kann den Nenner auch so schreiben: $$\begin{align} \text{Nenner} & = \Big(v_m^2 + (-v_p)^2 + 2v_m (-v_p) \cdot \cos((\omega_m - \omega_p) t)\Big)^\frac32 \\ & = \Big(v_m^2 + v_p^2 - 2v_m v_p \cdot \cos((\omega_m - \omega_p) t)\Big)^\frac32 \\ & = \Big( \overrightarrow{v_m}(t) + \overrightarrow{v_p}(t) \Big)^{2*\frac32} = \overrightarrow{v_{eff}}(t)^3 \end{align}$$ Solange die Geschwindigkeiten $v_p$ und $v_m$ unterschiedlich groß sind ist der Nenner positiv und verzerrt nur je nach Dynamik die Cosinus-Schwingung des Zählers. Wenn sie aber gleich sind, dann wird einmal pro Periode der Nenner zu Null und damit die Krümmung unendlich, d.h. es bildet sich in der Mondbahn eine zur Sonne gerichtete Spitze, weil der Mond am sonnennächsten Punkt der Bahn zum Stillstand kommt. Die Bedingung für solche Spitzen ist also: $$\begin{align} v_m & = v_p \\ \frac{2\pi r_m}{T_m} & = \frac{2\pi r_p}{T_p} \\ \frac{r_m}{r_p} & = \frac{T_m}{T_p}\tag{6} \end{align}$$ Damit kommen wir zur Periode $t_p$, die sowohl im Zähler wie im Nenner gleichermaßen auftritt. Die Frage ist: bei welchem Wert von $t$ wird das Argument vom Cosinus gleich $2\pi$? $$\begin{align} (\omega_m-\omega_p)\cdot t_p & = 2\pi \\ \bigg(\frac{2\pi}{T_m}-\frac{2\pi}{T_p}\bigg)\cdot t_p & = 2\pi \\ \bigg(\frac{T_p-T_m}{T_m\cdot T_p}\bigg)\cdot t_p & = 1 \\ t_p & = \frac{T_m\cdot T_p}{T_p-T_m}\tag{7} \end{align}$$ So wird beispielsweise aus dem siderischen Monat $T_m = 27,3217$ Tage und dem siderischen Jahr $T_p = 365,256$ Tage die Periode des synodischen Monats $t_p = 29,5306$ Tage.
Bei den meisten Monden geht diese Rechnung auf, aber wenn ein Mond an einem der Lagrange-Punkte verweilt, gibt es Ärger. Dann wird wegen Gleichheit von $T_m$ und $T_p$ der Nenner zu Null und damit die Periode zu unendlich. Man hat also keine Veränderung in der Krümmung. Die Bahn ist ein Kreis. Da dann die Bahnradien von Planet und Mond immer den gleichen Winkel bilden (und nicht wie sonst periodisch umlaufen), kann man die immer konstante Bahnkrümmung nur korrekt berechnen, wenn dieser konstante Winkel mit berücksichtigt wird. Für L2 sind die Radien in gleicher Richtung und man kann in die Krümmungsformel den positiven Mondbahnradius ($r_m\cdot cos(0°)=r_m$) und $t=0$ einsetzen. Für L1 ist der Winkel 180° und man setzt für den Mondbahnradius einen negativen Wert ein ($r_m\cdot cos(\pi)=-r_m$). Die drei restlichen Punkte L3, L4 und L5 müssten mit $r_m=0$ in die Krümmungsformel eingesetzt werden.
Das leitet zur Frage nach den Extremwerten der Krümmung über. Bei unterschiedlichen Werten von T ist der größte Wert des Kosinus-Terms im Zähler bei $t=0$ weil $\cos(0)=1$ und der kleinste bei $t=\frac12t_p=\frac{T_m\cdot T_p}{2(T_p-T_m)}$ weil $\cos(\pi)=-1$.
Zuletzt ist noch die Frage nach dem Übergang von einer rein konvexen Kurve (Zähler immer positiv) zu einer wellenförmigen Kurve (Zähler im Wechsel positiv und negativ). Das ist dann der Fall, wenn der minimale Zählerwert gleich Null ist. Es tritt ein, wenn A = B ist. $$\begin{align} A& = B \\ \omega_m v_m^2 + \omega_p v_P^2 & = v_m v_p\cdot(\omega_m + \omega_p) \\ \omega_m v_m\cdot(v_m-v_p)& = \omega_p v_p\cdot(v_m-v_p) \\ \omega_m v_m & = \omega_p v_p \\ \omega_m^2 r_m & = \omega_p^2 r_p \\ \frac{r_m}{T_m^2} & = \frac{r_p}{T_p^2} \\ \frac{r_m}{r_p} & = \bigg(\frac{T_m}{T_p}\bigg)^2\tag{8} \end{align}$$
3.) Zusammenfassung der Kurvenformen mit einer aktiven Grafik
Folgende Tabelle 1 gibt eine Überblick über die möglichen Bahnformen. Das feste Verhältnis von $r_m:r_p$ ist mit $1:9$ im Vergleich mit realen Planet-Mond-Systemen ($r_{Mond}:r_{Erde} = 1:390$) recht groß gewählt, damit die charakteristischen Merkmale auch beim Blick auf einen vollen Planetenumlauf noch gut erkennbar sind. Die Bilder können mit einem Klick auf die entsprechende Bahnform angezeigt werden.| Bahnform | Bedingung | |
|---|---|---|
| Schleife | $\frac{r_m}{r_p}\gt\frac{T_m}{T_p}$ | |
| Spitze | $\frac{r_m}{r_p}=\frac{T_m}{T_p}$ | |
| Welle | $\big(\frac{T_m}{T_p}\big)^2\lt\frac{r_m}{r_p}\lt\frac{T_m}{T_p}$ | |
| $\kappa_{min}=0$ | $\frac{r_m}{r_p}=\big(\frac{T_m}{T_p}\big)^2$ | |
| konvex | $\frac{r_m}{r_p}\lt\big(\frac{T_m}{T_p}\big)^2$ | |
| Kreis | $T_m=T_p$ |
Tabelle 1
4.) die Berechnungen der Rätselfragen 1.) und 2.)
Zunächst werden alle gegebenen Daten in die folgende Tabelle 2 geschrieben.
Dabei ist es wichtig, dass pro System die Dimension der Zeiten und der Radien jeweils gleich gewählt sind.
Ansonsten sind Zeiten und Radien in der Wahl der Dimensionen voneinander unabhängig.
Man wählt die Dimension der Zeiten so, wie man sie auch als Ergebnis für die Periode wünscht.
Die gewählte Dimension der Radien findet sich als Kehrwert der Dimensionen der Krümmungen wieder.
| Mond | Radien | Umlaufzeiten | ||||
|---|---|---|---|---|---|---|
| $r_p$ | $r_m$ | $[r]$ | $T_p$ | $T_m$ | $[T]$ | |
| Erdmond | 1,000000 | 0,00256667 | AE | 365,256 | 27,3217 | Tage |
| ISS | 1,000000 | 0,0000451867 | AE | 525969 | 92,0000 | min |
| geostationär | 1,000000 | 0,000281093 | AE | 365,256 | 0,997270 | Tage |
| SOHO in L1 | 1,000000 | -0,01000000 | AE | 1,000000 | 1,000000 | Jahre |
| WMAP in L2 | 1,000000 | 0,01000000 | AE | 1,000000 | 1,000000 | Jahre |
Tabelle 2
Mit dem Einsetzen obiger Daten in die Krümmungsformel (4) unter Berücksichtigung der oben gezeigten Formeln für $\omega$ und $v$
und mit $t=0$ für maximale Krümmung und $t=t_p/2$ für minimale Krümmung, ergibt sich folgende Tabelle 3, die die Antworten auf Rätselfrage 1.) und 2.) zeigt.
| Mond | Periode | Krümmung | |||
|---|---|---|---|---|---|
| $t_p$ | $[t_p]$ | $κ_{max}$ | $κ_{min}$ | $[\kappa]$ | |
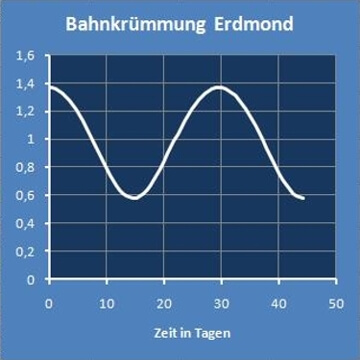
| Erdmond | 29,5306 | Tage | 1,36354 | 0,580427 | 1/AE |
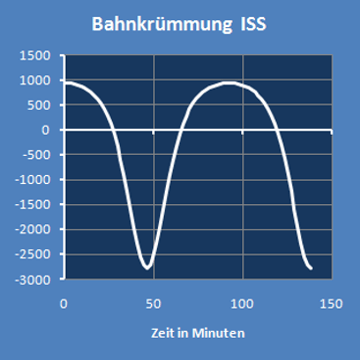
| ISS | 92,0161 | min | 933,376 | -2683,15 | 1/AE |
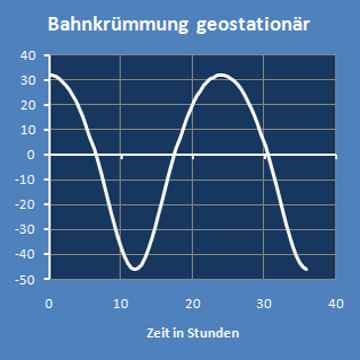
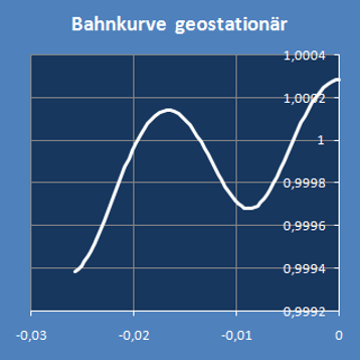
| geostationär | 1,000000 | Tage | 31,8182 | -45,6159 | 1/AE |
| SOHO in L1 | - | Jahre | 1,01010 | 1,01010 | 1/AE |
| WMAP in L2 | - | Jahre | 0,990099 | 0,990099 | 1/AE |
Tabelle 3
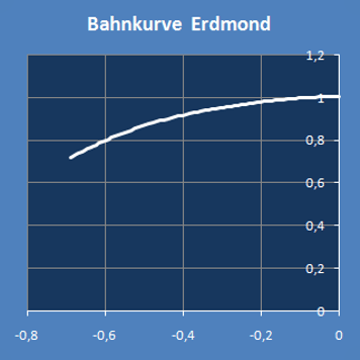
Wenn man für jeweils etwas mehr als eine Periodenlänge den Graph der Krümmung (unten links) und den Kurvenverlauf (unten rechts) darstellt,
hat man eine Übersicht über die Veränderlichkeiten.
Bei den Satelliten in L1 und L2 gibt es bei der Krümmung keine Veränderung und die Bahnkurve ist ein Kreis.
Deshalb sind diese Grafiken uninteressant und weggelassen.
Die Koordinatenachsen rechts sind in verschiedenen Maßstäben skaliert.
Dadurch ergibt sich im Bild eine hohe räumliche Auflösung, aber das verzerrt auch den Kurvenverlauf.
 |  |
 |  |
 |  |
5.) die Berechnungen der Rätselfrage 3.)
Die Frage 3.) erfordert den Einsatz des 3. Keplerschen Gesetzes: $$\Bigg(\frac{T_1}{T_2}\Bigg)^2 = \Bigg(\frac{r_1}{r_2}\Bigg)^3\tag{9}$$ Im Gravitationsfeld der Erde haben zwei Monde, oben in Gleichung (9) mit Index 1 und 2 bezeichnet, diese Bedingung zu erfüllen. Nimmt man als Referenz den Erdmond mit Radius $r_m$ und Umlaufzeit $T_M$ und bezeichnet man die Daten des gesuchten Mondes mit $r_x$ und $T_x$, so fehlt nur noch eine zusätzliche Bedingung, um das Gleichungssystem nach $r_x$ aufzulösen. Diese Bedingung ist die Kurvenform mit $\kappa_{min}=0$: $$\begin{align} \Bigg(\frac{T_m}{T_x}\Bigg)^2 & = \Bigg(\frac{r_m}{r_x}\Bigg)^3\tag{3. Keplersches Gesetz} \\ \frac{r_x}{r_p} & = \Bigg(\frac{T_x}{T_p}\Bigg)^2\tag{Kurvenbedingung aus Tabelle 1} \\ T_x^{\;2} & = T_p^{\;2}\cdot\frac{r_x}{r_p}\tag{Kurvenbedingung nach $T_x^{\;2}$ aufgelöst} \\ \frac{r_p}{r_x}\cdot\Bigg(\frac{T_m}{T_p}\Bigg)^2 & = \Bigg(\frac{r_m}{r_x}\Bigg)^3\tag{$T_x^{\;2}$ in 3. Keplersches Gesetz eingesetzt} \\ \frac{r_x^{\;\;3}}{r_x} & = \frac{r_m^{\;\;3}T_p^{\;2}}{r_pT_m^{\;\;2}}\tag{umsortiert} \\ r_x & = \frac{r_mT_p}{T_m}\cdot\sqrt{\frac{r_m}{r_p}} \\ \end{align}$$ $$ r_x = \frac{0,00256667\cdot 365,256}{27,3217}\cdot\sqrt{\frac{0,00256667} {1,000000}}\;AE\tag{Zahlen aus Tabelle 2} $$ $$\rand{\begin{align} r_x & = 0,00173838\;AE=260757\;km \\ T_x & = 15,2289\;Tage \end{align}}\tag{Antwort auf Frage 3.)}$$
6.) die Berechnungen der Rätselfrage 4.)
Die Vorgehensweise ist ähnlich wie bei der Frage 2.), nur die Bedingung ist eine andere und nicht der Mondbahnradius wird verändert sondern der Erdbahnradius. $$\begin{align} \Bigg(\frac{T_e}{T_x}\Bigg)^2 & = \Bigg(\frac{r_e}{r_x}\Bigg)^3\tag{3. Keplersches Gesetz} \\ \frac{r_m}{r_x} & = \frac{T_m}{T_x}\tag{Kurvenbedingung aus Tabelle 1} \\ T_x & = T_m\cdot\frac{r_x}{r_m}\tag{Kurvenbedingung nach $T_x$ aufgelöst} \\ \Bigg(\frac{T_er_m}{T_mr_x}\Bigg)^2 & = \Bigg(\frac{r_e}{r_x}\Bigg)^3\tag{$T_x$ in 3. Keplersches Gesetz eingesetzt} \\ \frac{r_x^{\;\;3}}{r_x^{\;\;2}} & = \frac{r_e^{\;3}T_m^{\;\;2}}{r_m^{\;\;2}T_e^{\;2}}\tag{umsortiert} \\ r_x & = \frac{r_e^{\;3}T_m^{\;\;2}}{r_m^{\;\;2}T_e^{\;2}} \\ \end{align}$$ $$ r_x = \frac{1,000000\cdot 746,475} {0,878890\cdot1,000000}\;AE\tag{Zahlen aus Tabelle 2} $$ $$\rand{\begin{align} r_x & = 849,339\;AE=127401\;Mio\;km \\ T_x & = 24752,6\;Jahre \end{align}}\tag{Antwort auf Frage 4.)}$$
Diese Informationen wurden zusammengestellt von