1.) Einleitung
Nicht nur weil bei den Rätselfragen keine Angaben über Abmessungen der Pyramide gemacht worden sind,
sind diese überflüssig.
Es ist leicht einzusehen, dass sich alle konstanten Skalierungsfaktoren wegkürzen würden.
Gleichgültig wie groß die Pyramide ist, wird die gefragte Bauhöhe in Prozent die gleiche sein.
Das gilt auch für das Verhältnis von Basislänge zu Höhe.
Sogar die Form der Grundfläche ist beliebig, z.B. rund in Kegelform,
nur muss die Volumenformel gelten:
$$\sand{
Volumen=Grundfläche \cdot Höhe /3
}\tag{1}$$
Deshalb wähle ich die einfachste Pyramide aus (mittleres Bild oben):
quadratische Grundfläche mit Kantenlänge a = 1 und Gesamthöhe hg = 1.
Das Volumen ist dann
$$\sand{
V_{Pyramide}=\frac{a^2\cdot h_g}3=\frac13
}\tag{2}$$
2.) die Volumenfunktion
Die Rätselfragen zielen auf eine bestimmte Bauhöhe.
Der bis dahin schon fertige Teil der Pyramide ist dann ein Pyramidenstumpf.
Das Volumen als Funktion der Bauhöhe x ist
$$\sand{
V_{Pyramidenstumpf}(x)=\intop_0^x(1-h)^2 dh=\frac{x^3}{3}-x^2+x
}\tag{3}$$
Darin ist (1-h) die mit der Bauhöhe h linear abnehmende Kantenlänge auf der jeweiligen Höhe.
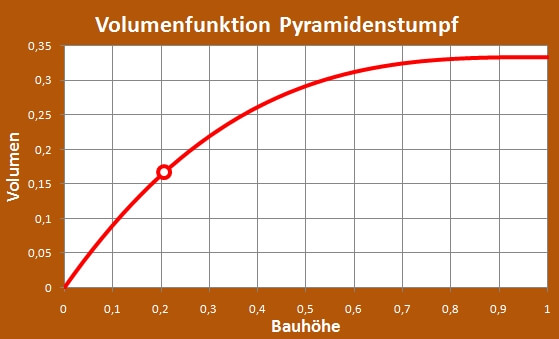
Der Funktionsverlauf sieht so aus:
Die Markierung (roter Kreis) zeigt die Position des halben Volumens und die zugehörige Bauhöhe an.
Hier folgt nun die Berechnung, basierend auf der
Cardanischen Formel zur Lösung kubischer Gleichungen:
$$\sand{\begin{align}
V_{Pyramidenstumpf}(x)-\frac12 V_{Pyramide}=0 \\
\frac{x^3}{3}-x^2+x-\frac16=0 \\
x^3-3x^2 +3x-0,5=0 \\
x=y+1 \\
(y+1)^3-3(y+1)^2+3(y+1)-0,5=0 \\
y^3+3y^2+3y+1-3y^2-6y-3+3y+3-0,5=0 \\
y^3+0,5=0 \\
y=\root 3 \of{-0,5} \\
x=1+\root 3 \of{-0,5} \\
x=1-\root 3 \of{0,5}=0,2062994740\end{align}}\tag{4}$$
Damit ist die Rätselfrage 1.) beantwortet: $\rand{20,6299474016\;\%}$
3.) die Funktion der Hubarbeit
Die Hubarbeit als Funktion der Bauhöhe x hat große Ähnlichkeit mit der Volumenfunktion.
Es kommt im Integral nur noch ein Faktor hinzu,
der die Masse, vertreten durch das Volumen, durch Anheben um h mit Hubarbeit beaufschlagt.
Auch hier können Konstante wie spezifisches Gewicht und Erdbeschleunigung weggelassen werden, da das Ergebnis ein Verhältnis ist.
Die Funktion ist somit als normiert zu betrachten, bei der die Konstanten auf 1 gesetzt werden.
$$\sand{
W_{Hubarbeit}(x)=\intop_0^x h(1-h)^2 dh=\frac{3x^4-8x^3+6x^2}{12}
}\tag{5}$$
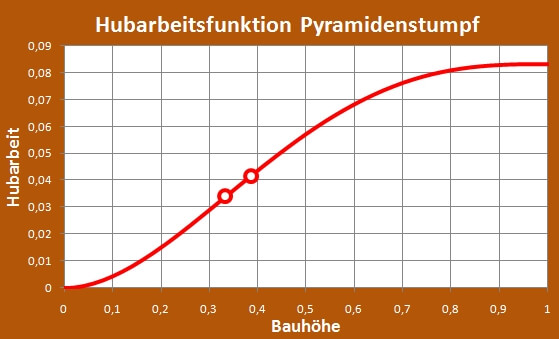
Der Funktionsverlauf sieht so aus:
Es gibt auf dem Kurvenverlauf zwei kreisförmige Markierungen.
Die linke gibt den Wendepunkt an.
Dort dreht die Steigung von zunehmend auf abnehmend.
Darauf wird im nächsten Abschnitt noch näher eingegangen.
Die rechte Markierung zeigt auf den Punkt der halben Hubarbeit.
Man kann versuchen, so wie oben eine Berechnung durchzuführen.
$$\sand{\begin{align}
W_{Hubarbeit}(x)-\frac12 W_{Hubarbeit}(1)=0 \\
3x^4-8x^3+6x^2-\frac12=0
\end{align}}\tag{6}$$
Hier endet zunächst der klassische Weg zur Bestimmung von x, nicht weil es keine Möglichkeiten mehr gibt,
sondern weil in heutiger Zeit mit Computerunterstützung Näherungsverfahren wesentlich einfacher zu handhaben sind.
Wer aber trotzdem den beschwerlichen Weg über die Lösung von biquadratischen Gleichungen gehen will, kann auf
dieser Wikipedia-Seite nachlesen
wie es der italienische Mathematiker Lodovico Ferrari (1522-1565) vorgemacht hat.
Hier benutze ich das Newton-Verfahren
$$\sand{
x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}
}\tag{7}$$
Dazu ist noch die Ableitungsfunktion von $W_{Hubarbeit}(x)$ zu berechnen.
Diese kann man direkt aus dem Integral (5) ablesen:
$$\sand{
W'_{Hubarbeit}(x)=x(1-x)^2
}\tag{8}$$
In der folgenden Tabelle sind die Näherungsschritte zu sehen.
Für den Anfangswert kann man aus dem Diagramm x0 = 0,38 ablesen,
für die erste Ableitung $f'(x_0)=x_0(1-x_0)^2=0,146072$.
| $n$ | $x_n$ |
|---|
| 0 | 0,380000000000000 |
| 1 | 0,385717454406046 |
| 2 | 0,385727531803988 |
| 3 | 0,385727568001777 |
| 4 | 0,385727568131920 |
| 5 | 0,385727568132388 |
| 6 | 0,385727568132390 |
Damit ist die Rätselfrage 3.) beantwortet: $\rand{38,5727568132\;\%}$
4.) die Funktion des Aufwands für die Hubarbeit
Die Funktion des Aufwands für die Hubarbeit ist nichts anderes als die von (8) schon bekannte Ableitung der Funktion der Hubarbeit.
In Anlehnung an die Beziehung zwischen Arbeit $W(t)$ und Leistung $P(t)$
$$\sand{
P(t)=\frac{d}{dt} W(t)
}\tag{9}$$
kann man auch die Ableitung der Hubarbeit als Hubleistung bezeichnen.
Es ist zwar keine Ableitung nach der Zeit sondern nach der Höhe,
aber wenn man die beim Bau zunehmende Höhe auch als Zeitablauf betrachtet, ist die Analogie verständlich.
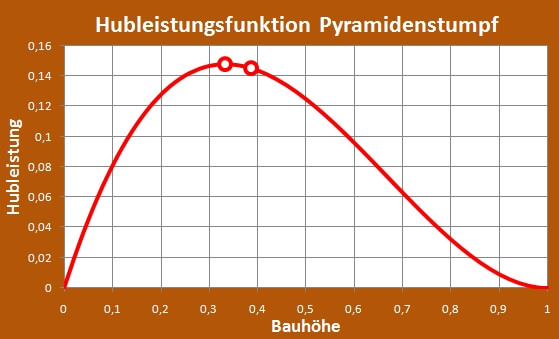
Hier ist der Funktionsverlauf mit den beiden Markierungen wie bei der Funktion der Hubarbeit.
Die Markierung am höchsten Punkt des Kurvenverlaufs ist das gesuchte Maximum.
Zur Berechnung ist diese Funktion nochmal abzuleiten:
$$\sand{
W''_{Hubarbeit}(x)=(x-1)\cdot(3x-1)
}\tag{10}$$
Die Ableitung wird gleich Null gesetzt und nach der gesuchten Höhe x aufgelöst:
$$\sand{\begin{align}
(x-1)\cdot(3x-1)&=0 \\
x_1&=\frac13 \\
x_2&=1
\end{align}}\tag{11}$$
Nur die Lösung x1 ist ein Maximum und damit ist die Rätselfrage 2.) beantwortet: $\rand{33,3333333333\;\%}$
Diese Informationen wurden zusammengestellt von